【통계학】 14-7강. Kolmogorov-Smirnov 검정
14-7강. Kolmogorov-Smirnov 검정
추천글 : 【통계학】 14강. 통계적 검정
1. 일반적인 Kolmogorov-Smirnov 검정 [본문]
2. 모수적 Kolmogorov-Smirnov 검정 [본문]
3. Cramér–von Mises 검정 [본문]
4. Kolmogorov-Smirnov 이표본 검정 [본문]
5. Kolmogorov-Smirnov 독립 검정 [본문]
1. 일반적인 Kolmogorov-Smirnov 검정 [목차]
⑴ 표본 (즉, empirical) 분포함수를 다음과 같이 정의함 : 계단함수 형태

⑵ two-sided Kolmogorov-Smirnov test는 다음 값이 클 경우 귀무가설을 기각함

Figure. 1. Kolmogorov-Smirnov 검정 통계량
⑶ 귀무가설
① D의 귀무분포는 F0 (연속적이라고 가정함)에 의존하지 않으며, 이는 다양한 표본 크기 n에 대해 표로 정리됨
② 즉, 귀무가설은 F hat과 F0, 두 확률분포가 동일하다는 것
⑷ 이론 : 귀무가설 하에서, √n D는 점근적으로 (n → ∞) Brownian bridge의 절댓값의 최댓값의 분포를 따름
⑸ 시뮬레이션 : Monte Carlo 시뮬레이션을 통해 p-value를 계산할 수 있음
① 실제로 귀무분포에서의 D의 분포는 F0에 의존하지 않기 때문에, 이는 각 표본 크기에 대해 한 번만 수행하면 됨
② 예를 들어, F0 = Unif(0, 1)로 둘 수 있음
2. 모수적 Kolmogorov-Smirnov 검정 [목차]
⑴ 통계량은 다음과 같이 정의됨
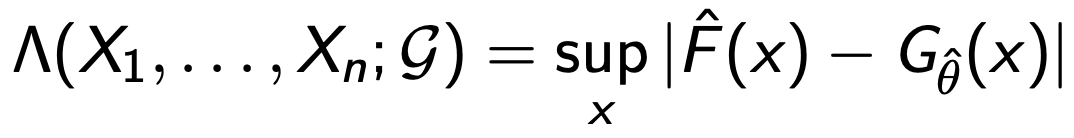
⑵ p-value는 일반적으로 parametric boostrap을 통해 추정됨 : 여기서 F hat과 θ hat은 각 부트스트랩 샘플에 대해 다시 계산
⑶ 𝒢가 정규 분포 계열인 경우 : 즉, 주어진 분포가 정규분포를 따르는지 검정하는 경우 (정규성 검정)
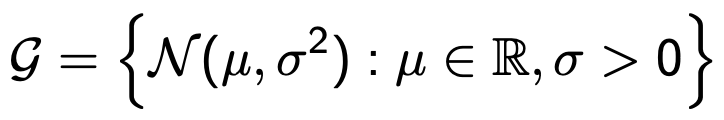
① 이 검정은 종종 Lilliefors normality test라고 불림
② 위의 통계량은 계열 내의 모든 분포에서 보정될 수 있으며, 이는 몬테카를로 시뮬레이션을 통해 수행
③ 따라서 이 통계량의 귀무분포는 표로 정리되어 있음
④ R 코드 : ks.test(dat, "pnorm", mean=mu, sd=sigma)
⑷ 동일한 논리가 다른 location-scale family의 분포에도 적용됨
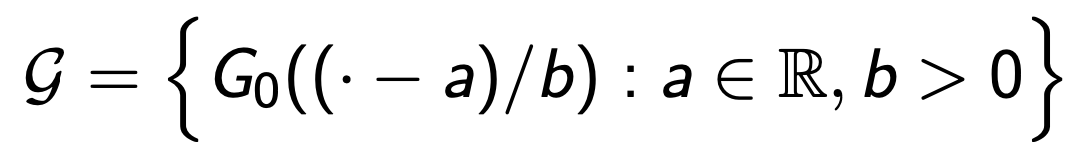
① 여기서 G0는 실수 집합 ℝ에서 정의된 주어진 분포
② location : 평균, 중앙값, 분위수 등
③ scale : 표준편차, MAD(median absolute deviation) 등
3. Cramér–von Mises 검정 [목차]
⑴ Kolmogorov-Smirnov 검정의 변형
⑵ Cramér–von Mises 검정은 다음 값이 클 경우 귀무가설을 기각
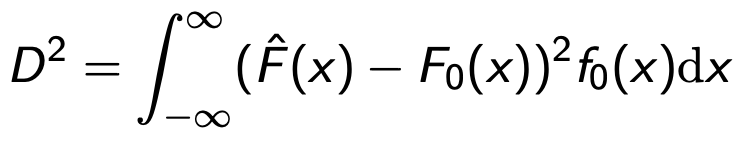
① f0(x) = dF0(x) /dx는 귀무가설 하의 확률밀도함수(PDF)
② MSE(mean-squared error)와 유사하게 식을 구성
⑶ 이는 적분 계산이 필요 없는 간단한 폐쇄형(closed form) 표현을 가짐
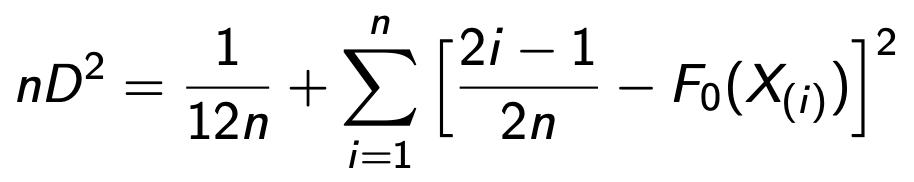
① 여기서 X(1) ≤ ⋯ ≤ X(n)은 순서 통계량(order statistics)으로 정렬된 샘플
② D의 귀무 분포(null distribution)는 F0에 의존하지 않으며 표로 작성되어 있음
③ 점근적 귀무 분포(asympotic null distribution)도 알려져 있지만 복잡함
④ 따라서 p-value를 계산하기 위해 Monte Carlo 시뮬레이션을 사용할 수 있음
4. Kolmogorov-Smirnov 이표본 검정 [목차]
⑴ (단측) Kolmogorov-Smirnov 검정은 아래 값이 클 때 귀무가설을 기각함
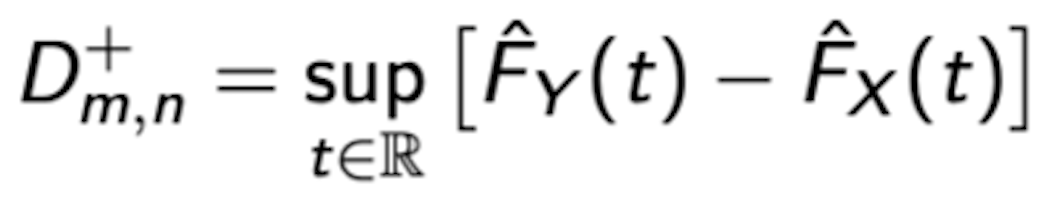
⑵ 이론
① Dm,n+의 분포는 몇 가지 재귀 공식들을 사용하여 정확하고 효율적으로 계산할 수 있음
② 큰 표본의 경우, 다음과 같은 극한 분포를 가짐
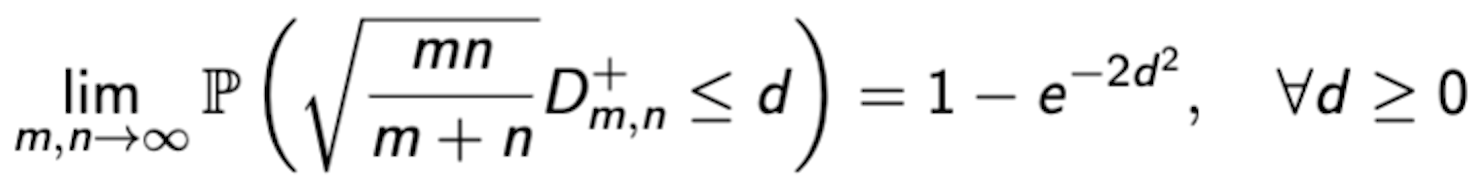
③ 위 분포는 표본 크기를 ⎣ mn / (m+n) ⎦로 한 단일 표본 검정에서의 극한 분포와 동일함
5. Kolmogorov-Smirnov 독립 검정 [목차]
⑴ 개요
① Kolmogorov-Smirnov 검정을 응용하여 Hoeffding이 1948년 empirical CDF를 이용해 두 확률변수의 독립을 검정하는 분석을 제안
② 특징 1. distribution-free : X와 Y가 연속이라면 분포에 관계 없이 이 분석을 사용할 수 있음. 닫힌 형태의 점근적 분포도 알려져 있음
③ 특징 2. universally consistent : 독립에 대한 임의의 대립가설에 대해서도 이 검정을 사용할 수 있음
⑵ 통계량

① 귀무가설 H0 : 두 확률변수가 독립
② H 값이 크면 귀무가설을 기각함
③ FnX : X1, ···, Xn의 empirical CDF
④ FnY : Y1, ···, Yn의 empirical CDF
⑤ FnXY : (X1, Y1), ···, (Xn, Yn)의 joint empirical CDF
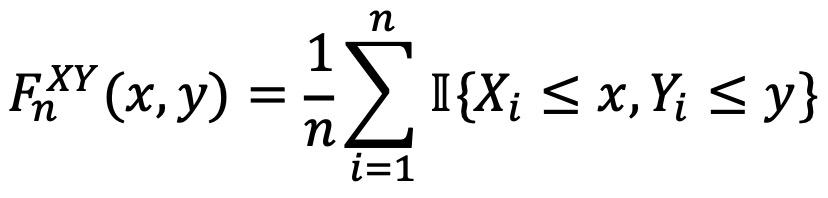
입력: 2025.03.23 18:32
