14강. 통계적 검정
추천글 : 【통계학】 통계학 목차
1. 용어 [본문]
2. 네이만-피어슨 보조정리 [본문]
3. 일반 우도비 검정 [본문]
4. p value [본문]
5. 통계적 검정의 종류 [본문]
1. 용어 [목차]
⑴ 검정(test)
① 정의 : 가설이 통계적으로 유의한지 알아보는 것
○ 응용 1. randomization check (balance test) : random sampling이 잘 됐는지 검증하는 것
○ 응용 2. causal effect : 특정 처리(treatment)가 유의미한 변화를 만드는지 검증하는 것
② 검정통계량(test statistic) : 상태공간의 n차원 정보를 1차원으로 요약하여 통계적 검정에 이용하는 것
○ 예 : Z, T, χ2, F 등
○ (참고) 1차원으로 요약 가능함은 기각역의 크기가 일정할 때 중요하게 작용
③ 모수적 검정(parametric test)
○ 정의 : 검정통계량을 통해 모수를 검정하는 것
○ 일반적으로 모집단의 분포가 정규분포라는 가정 : 중심극한정리를 이용
○ 실제로는 위 가정 없이 임의의 표본에 모수적 검정을 사용해도 크게 문제되지 않음
④ 비모수적 검정(non-parametric test)
○ 정의 : 검정통계량을 통해 비모수적 특성을 검정하는 것
○ 모집단의 분포를 특정할 수 없는 경우 (distribution-free method)
○ 모수적 방법에 비해 통계량의 계산이 간편하여 직관적으로 이해하기 쉬움
○ 이상값으로 인한 영향이 적음
○ 검정 통계량의 신뢰성이 부족함
⑵ 가설(hypothesis)
① 귀무가설(null hypothesis) (H0) : 현재까지 주장되어 온 것이거나 기존과 비교하여 변화 혹은 차이가 없음을 나타내는 가설
② 대립가설(alternative hypothesis) (H1) : 귀무가설이 기각될 때 받아들여지는 가설
○ 연구가설이라고도 함
③ 성질 : 모수(parameter) θ에 대해
○ H0 : Θ0 ={θ0, θ0', θ0'', ···}
○ H1 : Θ1 ={θ1, θ1', θ1'', ···}
○ 성질 1. p(θ ∈ Θ0 or θ ∈ Θ1) = 1
○ 성질 2. p(θ ∈ Θ0 and θ ∈ Θ1) = 0
④ 분류
○ 단순가설(simple hypothesis) : Θ ={θ0}, Θ ={θ1}인 경우
○ 복합가설(composite hypothesis) : 단순가설이 아닌 경우
○ 예. H0 : θ ≤ θ0, H1 : θ > θ0인 경우 복합가설임
⑶ 기각역 도입
① 상태공간(state space) = 기각역(critical region) + 나머지 공간(acceptable region)
○ 기각역 : 귀무가설을 기각시키는 검정통계량의 범위
○ 표본 ∈ 기각역 : H0 기각(reject)
○ 표본 ∉ 기각역 : H0 채택(not reject)
② 검정력 함수(power function) πC(θ) : 기각역이 C이고 모수가 θ일 때 표본이 기각역에 포함될 확률
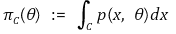
③ 검정력 함수 예
○ p(x) = 4x3 / θ4 I{0 < x < θ}
○ C ={x | x ≤ 0.5, x > 1}
○ θ ≤ 0.5
πC(θ) = 1
○ 0.5 < θ ≤ 1
πC(θ) = ∫ p(x) dx (단, x ∈ [0, 0.5] ) = 1 / 16θ4
○ 1 < θ
πC(θ) = ∫ p(x) dx (단, x ∈ [0, 0.5] ∪[1, θ] ) = 1 - 15 / 16θ4
④ 기각역의 크기 또는 검정의 크기(size) : 귀무가설이 참일 때 표본이 기각역에 포함될 확률의 최댓값

⑤ 검정력(power) : 대립가설이 참일 때 기각역에 포함될 확률 = 대립가설이 참일 때 귀무가설을 기각할 확률

⑥ 오류(error) : 잘못된 통계적 결론을 내리는 것
○ 이상적인 기각역
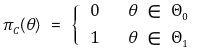
○ 제1종 오류(type Ⅰ error)
○ 정의 : 귀무가설이 참일 때 귀무가설을 기각하는 오류
○ 조건 : 귀무가설이 단순가설일 때 정의됨
○ 제1종 오류 확률(α) = 기각역의 크기
○ 유의수준(significance level) : 10%, 5%, 1% 등
○ 신뢰도(confidence level) : 90%, 95%, 99% 등
○ 제2종 오류(type Ⅱ error)
○ 정의 : 대립가설이 참일 때 귀무가설을 채택하는 오류
○ 조건 : 대립가설이 단순가설일 때 정의됨
○ 제2종 오류 확률(β) = 1 - 검정력
○ α와 β의 트레이드오프(trade-off)
Figure. 1. 제1종 오류(α)와 제2종 오류(β)의 교환조건
○ 기각역은 특정 값 이상 또는 특정 값 이하와 같은 구간으로 나타남 (∵ 네이만-피어슨 보조정리)
○ α와 β 모두 감소시킬 수는 없음
⑷ 기각역 비교
① 기준 : 기각역의 크기가 동일할 때 검정력이 더 클 것
② 강력 검정(more powerful testing) : 특정 θ1 ∈ Θ1과 두 기각역 C1, C2에 대해
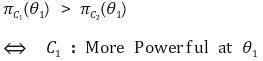
③ 최강력 검정(most powerful testing) : 특정 θ1 ∈ Θ1과 임의의 기각역 C에 대해
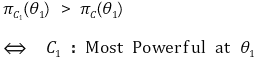
④ 균일 최강력 검정(uniformly most powerful testing) : 임의의 θ ∈ Θ1와 임의의 기각역 C에 대해

2. 네이만-피어슨 보조정리(Neyman-Pearson Lemma) [목차]
⑴ 발상
① 전제 : H0 : θ = θ0, H1 : θ = θ1 (단순가설)
② 문제 : 기각역의 크기가 일정할 때 검정력이 최대가 되는 기각역을 찾는 것
③ 고찰 : 상태공간(state space)에서 표본을 하나씩 기각역 C에 포함
○ 하나의 표본 x가 C에 들어가면 p(x, θ0)와 p(x, θ1)이 모두 증가
○ p(x, θ0) : 일종의 비용. p(x, θ0)의 증가는 기각역의 크기를 증가
○ p(x, θ1) : 일종의 이득, p(x, θ1)의 증가는 검정력을 증가
④ 결론
○ 줄세우기 전략 : p(x, θ1) ÷ p(x, θ0)이 가장 큰 것부터 기각역에 포함시키는 전략이 유리함
○ 줄세우기 전략으로 만든 기각역 C ={x | p(x, θ1) ÷ p(x, θ0) ≥ k}는 균일 최강력 검정 기각역
⑵ 정리
① 전제 : H0, H1는 단순가설임
② 내용 : 어떤 k ∈ ℝ에 대해 다음과 같이 기각역을 설정하면 균일 최강력 검정 기각역이 됨
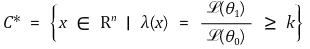
○ ℒ : 우도함수
○ 우도비 검정(LR test, likelihood ratio test) : λ(x) ≥ k와 같은 검정
○ 기각역의 결정 : 기각역의 정확한 형태를 알려면 기각역의 크기가 주어져야 함
○ λ(x) ≥ k를 만족하는 모든 x는 기각역 C*에 포함
○ λ(x) < k를 만족하는 모든 x는 기각역 C*의 여집합에 포함
③ 응용
○ p(x, θ1) ÷ p(x, θ0)의 순위만 일정하면 되므로 단조증가함수 f(·)에 대해 다음과 같은 변환이 허용

○ θ0, θ1, n 등과 관련된 항을 쉽게 제거할 수 있음
○ 의미 : k'의 존재성을 확보하는 한 기각역의 자유로운 변형이 허용됨
○ 기각역의 결정 : 기각역의 정확한 형태를 알려면 기각역의 크기가 주어져야 함
⑶ 증명
① 가정 : C*와 C의 크기(size)는 동일
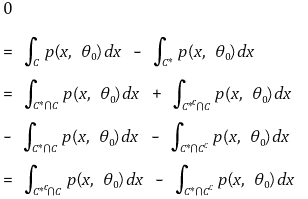
② C*의 정의

③ 결론 : C*는 균일 최강력 검정 기각역
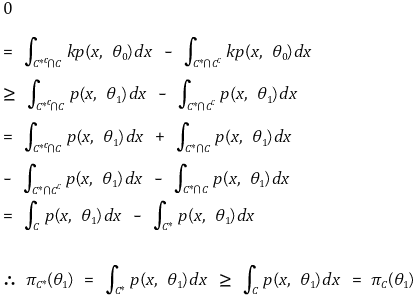
⑷ 예 1.
① X1, ···, Xn ~ Bernoulli(θ)
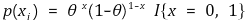
② H0 : θ = θ0, H1 : θ = θ1 > θ0
③ 우도비 검정
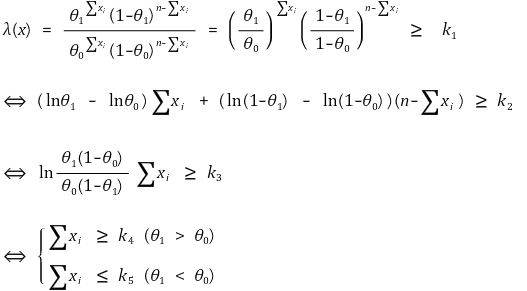
④ Z-test (신뢰도 : α)
○ θ1 > θ0 : 단측검정(one-tailed test)

○ θ1 < θ0 : 단측검정(one-tailed test)

○ θ0와 θ1의 대소에 따라 최강력 검정 기각역이 달라지므로 균일 최강력 검정 기각역이 존재하지 않음
⑸ 예 2.
① X1, ···, Xn ~ N(μ, 12)

② H0 : μ = μ0, H1 : μ = μ1 > μ0
③ 우도비 검정
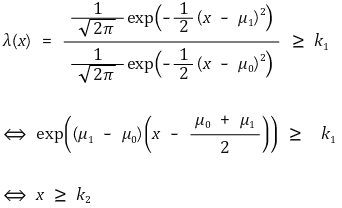
④ Z-test : 단측검정(one-tailed test) (신뢰도 : α)

⑹ 확장 1. 기각역이 θ1의 구체적인 값에 의존하지 않으면 H1이 복합가설이어도 기각역 형태는 동일
① X1, ···, Xn ~ Bernoulli(θ)
② H0 : θ = θ0, H1 : θ > θ0
⑺ 확장 2. 확장 1에서 대립가설이 θ0를 포함한 복합가설이고 θ0일 때 α가 최대인 경우 기각역 형태는 동일
① X1, ···, Xn ~ Bernoulli(θ)
② H0 : θ < θ0, H1 : θ > θ0
3. 일반 우도비 검정(generalized likelihood ratio test) [목차]
⑴ 정의
① 네이만-피어슨 보조정리의 한계 : 일반적으로 귀무가설과 대립가설이 단순가설이어야 함
② 일반 우도비 검정(GLR test, generalized likelihood ratio test) : 일반 우도비 도입
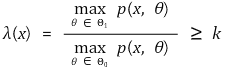
③ max p(x, θ)는 최대우도 추정법(ML, maximum likelihood method)을 이용
④ 통계적으로 나쁘지 않은 기각역을 설정함이 증명됨
⑵ 예 1. Xi ~ N(μ, σ2), σ2 is known
① H0 : μ = μ0, H1 : μ ≠ μ0
② 일반 우도비 검정
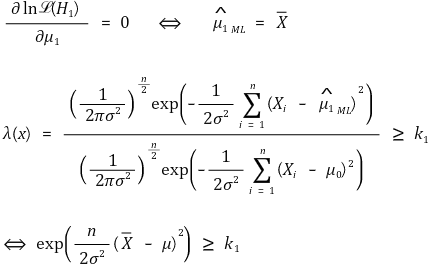
③ τ-test : 단측검정(one-tailed test) (신뢰도 : α)

④ Z-test : 양측검정(two-tailed test) (신뢰도 : α)

⑤ Xi가 정규분포를 따르지 않아도 위 방법을 근사적으로 적용 가능함이 증명됨
⑶ 예 2. Xi ~ N(μ, σ2), σ2 is unknown
① H0 : μ = μ0, H1 : μ ≠ μ0
② 일반 우도비 검정
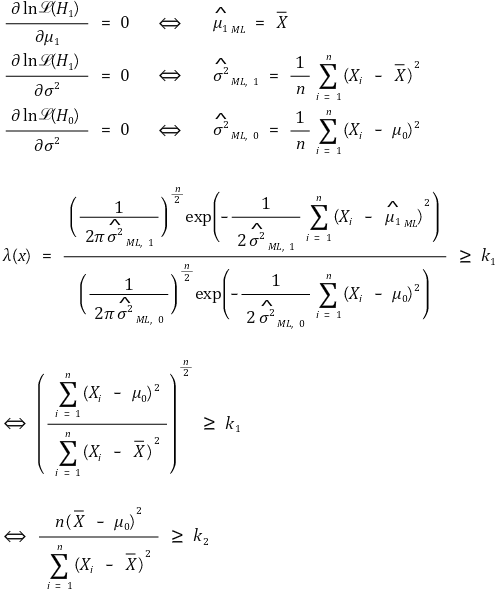
③ F-test : 단측검정(one-tailed test) (신뢰도 : α)
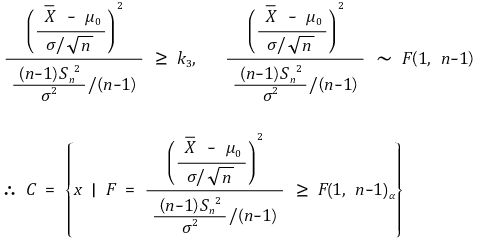
④ T-test : 양측검정(two-tailed test) (신뢰도 : α)

⑷ 예 3. Xi ~ N(μ, σ2), σ2 is unknown
① H0 : μ = μ0, H1 : μ > μ0
② 일반 우도비 검정
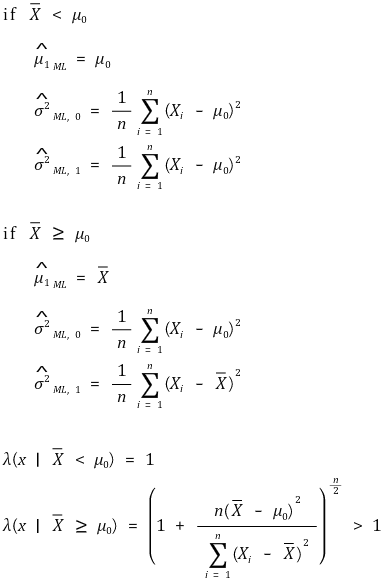
③ 중요 가정
○ Xavg ≥ μ0에서가 Xavg < μ0에서보다 우도비가 높으므로 줄세우기 전략에서 우선순위가 높음
○ 유의수준은 0.025, 0.05, 0.10 정도만 사용하므로 절반만큼은 있으리라 예상되는 Xavg ≥ μ0만 고려해도 충분함
④ T-test : 단측검정(one-tailed test) (신뢰도 : α)
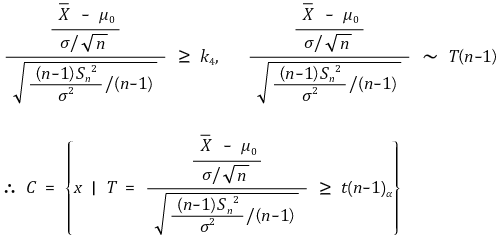
⑤ H1 : μ < μ0인 경우도 동일한 논리가 적용됨
⑸ 예 4. Xi ~ N(μ, σ2), μ is unknown
① H0 : σ2 = σ02, H1 : σ2 ≠ σ02
② 일반 우도비 검정

③ 기각역 설정
○ f(τ)는 τ = n에서 극솟값을 가지는 아래로 볼록한 함수
○ 조건 1. P(τ ≥ k' | H0) + P(τ ≤ k'' | H0) = α
○ 조건 2. f(k') = f(k'')

④ τ-test : 양측검정(two-tailed test) (신뢰도 : α)
○ 이상적인 기각역을 설정하려면 수치해석을 거쳐야 함
○ 실제로는 보다 단순화된 기각역이 사용됨

⑹ 예 5. 특수 우도비 검정
① 정의
○ Xi ~ N(μ, σ2), σ2 is known인 경우 2 ln λ ~ χ2(1)가 성립
○ Wilks’ phenomenon : 표본크기 n이 충분히 큰 경우 파라미터의 개수 k에 대해 다음이 수학적으로 증명돼 있음

② τ-test : 단순 가설에서의 단측검정(one-tailed test) (신뢰도 : α)

③ 증명

④ 예제
○ 예제 1. X1, ···, Xn ~ Poisson(λ)와 귀무가설 H0 : λ = λ0, H1 : λ ≠ λ0에 대하여 신뢰수준 α에 대한 기각역을 찾아라.

○ 예제 2. θ = (p1, ···, p5)에 대한 다항분포를 따르는 y1, ···, y5가 있어 L(θ) = p1y1 ··· p5y5와 같이 정의된다. 귀무가설 H0 : p1 = p2 = p3, p4 = p5와 대립가설 H1에 대하여, 신뢰수준 α에 대한 기각역을 찾아라.
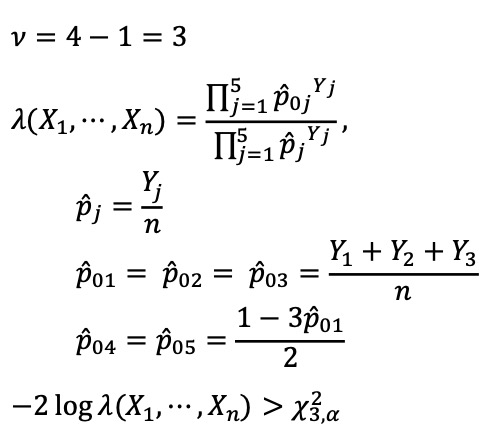
⑤ 보충
○ 일부 통계학자들은 이러한 검정에 한해 우도비 검정(LR test)으로 지칭
○ 일부 통계학자들은 -2 ln λ = 2 ln ℒ(H1) - 2 ln ℒ(H0)로 정의
4. p value [목차]
⑴ 정의 : 귀무가설이 참일 때 주어진 표본보다 더 극단적인 값이 나올 확률
① 또다른 정의 : 귀무가설이 사실일 확률
② 검정통계량이 기각역에 속하면 기각하는 것과 p value가 α보다 작으면 기각하는 것은 필요충분조건
③ 엄밀한 정의
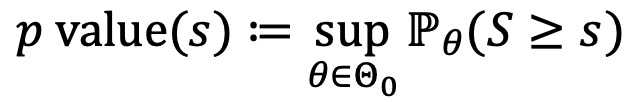
⑵ 계산 : θ*는 측정값
① 우측단측검정 : p value = P(θ ≥ θ*)
② 좌측단측검정 : p value = P(θ ≤ θ*)
③ μ를 중심으로 대칭 분포(symmetric distribution about μ) : p value = P(|θ - μ| ≥ |θ* - μ|)
④ 카이제곱분포 : θ*가 중앙값보다 큰 경우 p value = P(θ ≥ θ*), 작은 경우 p value = P(θ ≤ θ*)
⑶ 검정력과 p value
① (참고) 고전 통계학의 주요 이슈는 분포를 찾는 것과 검정력을 높이는 것
② 엄밀한 의미 : 검정력이 높다는 것은 α가 일정할 때 대립가설이 참이라면 귀무가설을 기각할 확률이 높다는 의미
③ α가 일정하다는 것의 의미
○ 여러 통계기법에서 얻어진 각 분포의 마지노선을 일정하게 정의하겠다는 의미
○ 주어진 표본 외에 다른 많은 경우의 수를 귀무가설이 참인 경우로 희생시킨다는 의미
④ 1-β를 증가시키는 것의 의미 : 여러 통계기법에서 마지노선에 대해 더 극단적으로 위치하게 만들겠다는 의미
⑤ 직관적 의미 : 검정력이 높인다는 것은 α가 일정할 때 p value가 더 작게 나오는 통계 기법을 사용하겠다는 의미
⑥ 예 1. 동일 표본에 대해 t 통계량보다 F 통계량을 쓰는 게 p value가 더 작음 → 검정력을 더 높임
⑦ 예 2. t 분포는 자유도가 클수록 더 좁아짐 → 검정력이 더 커짐
⑧ 통계 기법마다 검정력이 다름 : 동일한 통계자료에 대해 통계적 결론이 다를 수 있다는 의미
⑷ 예시 : 상관계수와 p value
① H0 : X와 Y는 상관관계가 없음
② p value의 의미 : 상관관계가 없는 모집단에서 추출한 표본집단의 상관계수가 주어진 상관계수보다 클 확률
③ 정규분포를 통한 p value 계산에 대한 가정
○ 임의 추출된 자료
○ 이변량 정규분포 : 각 변수 X, Y는 정규분포를 따름
○ 관계가 선형으로 나타나야 함 : 2차, 3차 등의 관계는 적합하지 않다는 의미
○ 위 세 조건을 만족하지 않으면 비모수검정을 통해 p value를 계산해야 함
⑸ 다중 검정 문제(multiple testing problem)
① 개요
○ p-value가 귀무가설 H0 하에서 균일분포라고 가정
○ 증명 : 귀무가설에서 S의 CDF를 F0라 하고, F0가 증가함수라고 하면,
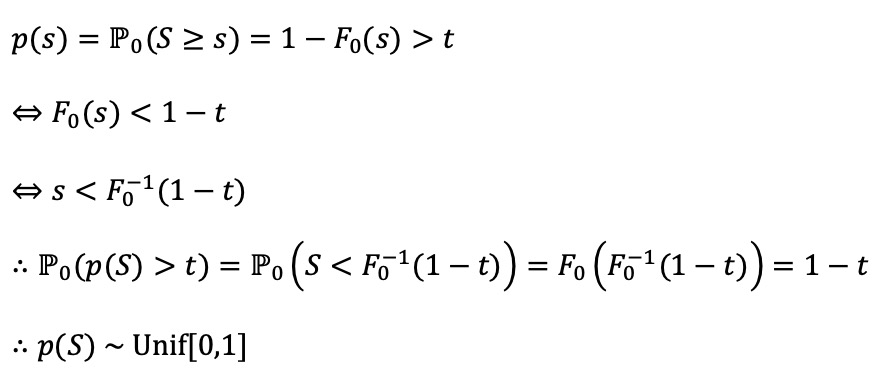
○ 문제 정의 : 1000개의 가설을 검정했고, 각각의 가설에서 p value가 α = 0.05보다 작을 때 귀무 가설을 기각했다고 가정하자. 이 경우, 귀무 가설을 잘못 기각할 것으로 예상되는 횟수는 몇 번일까? 답은 50번 정도 귀무 가설을 잘못 기각할 것으로 예상된다 (∵ 1000 × 0.05 = 50). 따라서 발견된 모든 기각된 가설을 유의미하다고 보고할 수는 없다.
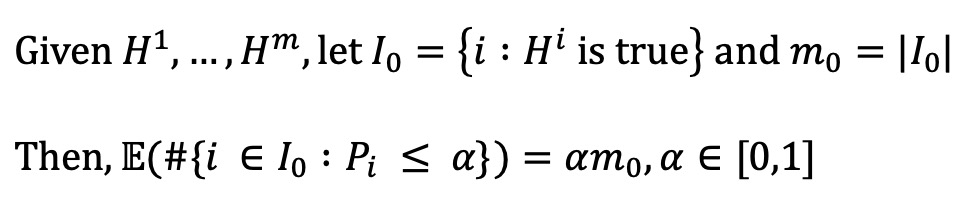
○ 즉, 여러 번 통계적 검정을 하는 행위 자체가 도출된 결론을 부정확하게 만듦
○ 예를 들어, 여러 유전자로 구성된 시퀀싱 데이터에서 DEG를 도출하는 과정에서 문제가 됨
② 해결방법 1. FWER(family-wise error rate) 제어
○ 정의 : 전체 가설 중 단 하나라도 잘못된 결론을 내릴 확률
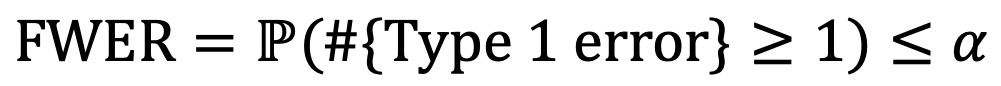
○ FWER이 5%라는 것은 여러 가설 검정에서 단 하나의 잘못된 결론을 내릴 확률이 5% 이하라는 의미로 매우 보수적이며 거짓 양성 결과를 거의 허용하지 않음
○ FWER은 많은 제2종 오류를 유발한다는 의미에서 검정력이 낮아지는 결과를 초래한다고 비판받기도 함
○ 종류 1. Sidak 보정 : p-value가 아닌 alpha 임계값을 조정하며, p-value들이 독립적일 때 사용
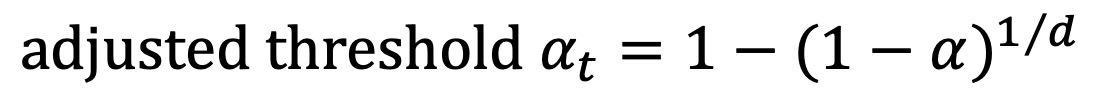
○ d : 통계적 검정 횟수
○ 종류 2. Bonferroni 보정 : 각각의 p-value를 직접 보정하며 p-value가 독립적이지 않아도 사용 가능. 매우 보수적

○ d : 통계적 검정 횟수
○ 단, adjusted p value > 1이면 1로 강제로 조정
○ 유의수준 α에서 FWER 증명
○ 통계적 검정의 횟수가 m이고 각 통계적 검정이 독립이라고 가정 (union bound 조건에 필요)
○ I0는 미리 정해져 있지만 알 수 없는 집합으로, p-value가 높은 귀무가설들로 주로 구성될 것으로 추정됨

○ 종류 3. Holm (step-down) 보정
○ 단계 1. p-value를 정렬 : P(1) ≤ ··· ≤ P(m)을 획득
○ 단계 2. P(r+1) > α / (m-r) (단, m은 통계적 검정의 횟수)을 만족하는 가장 작은 r ≥ 0을 R로 정의
○ 단계 3. R > 0이라면 귀무가설 H(1), ···, H(R)을 기각하고 R = 0이면 어떤 귀무가설도 기각하지 않음

○ 유의수준 α에서 FWER 증명
○ 통계적 검정의 횟수가 m이고 각 통계적 검정이 독립이라고 가정 (union bound 조건에 필요)
○ I0는 미리 정해져 있지만 알 수 없는 집합으로, p-value가 높은 귀무가설들로 주로 구성될 것으로 추정됨

○ α가 동일할 때 Holm이 Bonferroni보다 더 powerful

○ 종류 4. Hochberg (step-up) 보정
○ 단계 1. p-value를 정렬 : P(1) ≤ ··· ≤ P(m)을 획득
○ 단계 2. P(r) ≤ α / (m + 1 - r) (단, m은 통계적 검정의 횟수)을 만족하는 가장 큰 r ≥ 0을 R로 정의
○ 단계 3. R > 0이라면 귀무가설 H(1), ···, H(R)을 기각하고 R = 0이면 어떤 귀무가설도 기각하지 않음
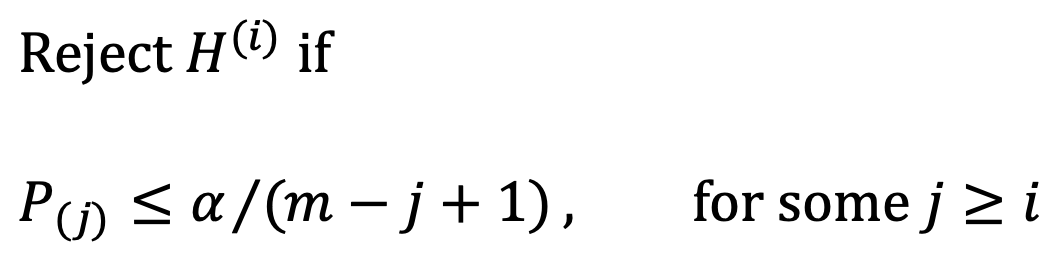
○ 유의수준 α에서 FWER 증명에 대한 직관적 이해
○ 통계적 검정의 횟수가 m이고 각 통계적 검정이 독립이라고 가정 (independence 조건에 필요)
○ I0는 미리 정해져 있지만 알 수 없는 집합으로, p-value가 높은 귀무가설들로 주로 구성될 것으로 추정됨
○ m - j0 + 1 ≥ m0가 반드시 성립한다고 볼 수 없으므로 다음 수식 전개는 참고용으로만 확인할 것
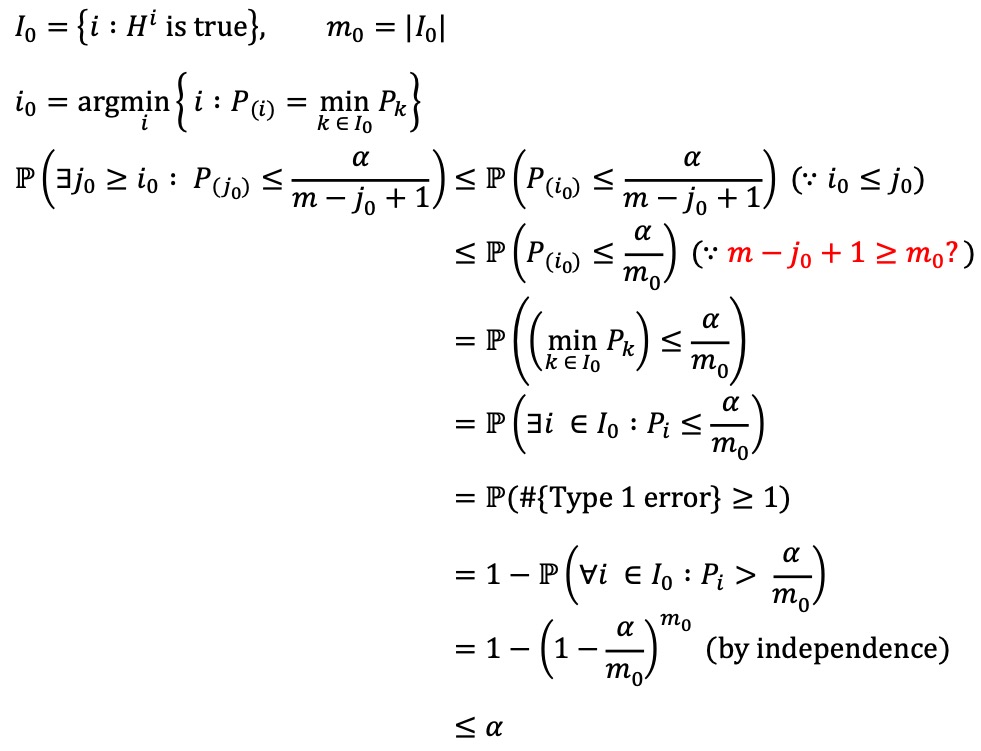
○ α가 동일할 때 Hochberg가 Holm보다 더 powerful
○ 직관적 이해 : Holm은 "for all" 조건이고 Hochberg는 "for some" 조건
○ 종류 5. Tukey-Kramer honest significant difference (range test)
○ 다중 샘플 상황에서 모든 쌍별 비교(pairwise comparison)를 수행할 때 사용
○ 귀무가설 : Hjk : μj = μk
○ J개의 샘플 (Yij : i = 1, ···, nj), j = 1, ···, J
○ N = n1 + ··· + nJ
○ μj : 그룹 j의 모평균
○ 통계량 : 유의수준 α에서 다음을 만족하면 Tukey-Kramer는 Hjk를 기각

○ 이론 : 샘플들이 서로 독립이고, 정규 분포를 따르며, 분산이 동일하고 샘플 수가 같을 경우, Tukey-Kramer 검정은 유의수준 α에서 FWER을 정확히 제어
③ 해결방법 2. FDR(false discovery rate) 제어
○ 개요
○ 정의 : 실제 기각된 가설 중에서 귀무가설이 포함될 확률(FDR, type 1 error의 비율)을 일정 수준 이하로 제한하는 방법

○ FWER 제어는 FDR 제어를 암시함
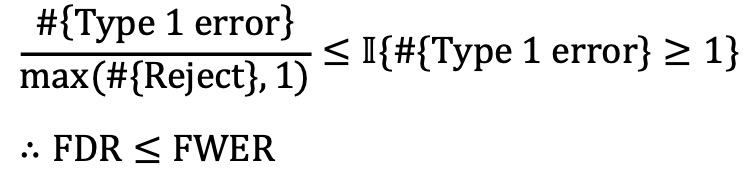
○ H0, H1 하에서의 p-value distribution을 모두 고려하여 덜 conservative 하게 통계적 검정을 할 수도 있음
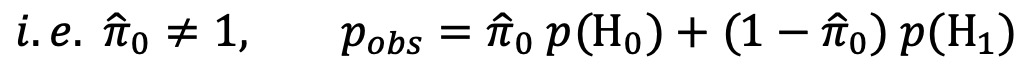
○ 종류 1. Benjamini–Hochberg (B&H) : 테스트들의 상관관계가 단순할 때 사용
○ 단계 1. p-value를 정렬 : P(1) ≤ ··· ≤ P(m)을 획득
○ 단계 2. P(r) ≤ rα / m (단, m은 통계적 검정의 횟수)을 만족하는 가장 큰 r ≥ 0을 R로 정의
○ 단계 3. R > 0이라면 귀무가설 H(1), ···, H(R)을 기각하고 R = 0이면 어떤 귀무가설도 기각하지 않음

○ Hotchberg와 유사한 step-up 과정이지만 역치값이 다름
○ Hotchberg : P(j)와 α / (m - j + 1)을 비교함
○ Benjamini-Hotchberg : P(j)와 j α / m을 비교함
○ 유의수준 α에서 FDR 증명에 대한 직관적 이해
○ 각 통계적 검정이 독립이라고 가정

○ adjusted p value
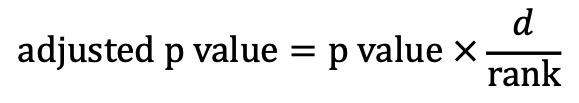
○ d : 통계적 검정 횟수
○ rank : p value들의 정렬 순위
○ 단, adjusted p value > 1이면 1로 강제로 조정
○ 더 낮은 rank (e.g., rank = 1)가 더 낮은 p value가 되도록 해야 하며 안 맞을 경우 이를 조절하는 단계가 있음
○ B&H 검정 예시 : 유의수준 α, 통계적 검정 횟수 m, i 번째로 낮은 p-value인 p(i)에 대하여,

| gene | p-val | rank | initial adj p-val | final adj p-val |
| A | 0.039 | 3 | 0.039 × (25/3) = 0.325 | 0.21 |
| B | 0.001 | 1 | 0.001 × (25/1) = 0.025 | 0.025 |
| C | 0.041 | 4 | 0.041 × (25/4) = 0.256 | 0.21 |
| D | 0.042 | 5 | 0.042 × (25/5) = 0.21 | 0.21 |
| E | 0.008 | 2 | 0.008 × (25/2) = 0.1 | 0.1 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
Table. 1. B&H 검정 예시 (25 genes)
○ 종류 2. Benjamini–Yekutieli (B&Y) : 테스트들의 상관관계가 복잡할 때 사용
○ 각 통계적 검정이 독립이 아니어도 Benjamini-Yekutieli는 유의수준 α에서 FDR을 제어
○ adjusted p value

○ d : 통계적 검정 횟수
○ rank : p value들의 정렬 순위
○ ∑(i = 1 to d) 1 / i : 조정된 상수. 테스트들의 상관관계를 고려하여 좀 더 보수적으로 FDR을 제어하기 위한 항
○ 단, adjusted p value > 1이면 1로 강제로 조정
④ adjusted p value : 서로 다른 보정 방법에 대해 동일한 유의수준 α를 적용하기 위해 도입됨
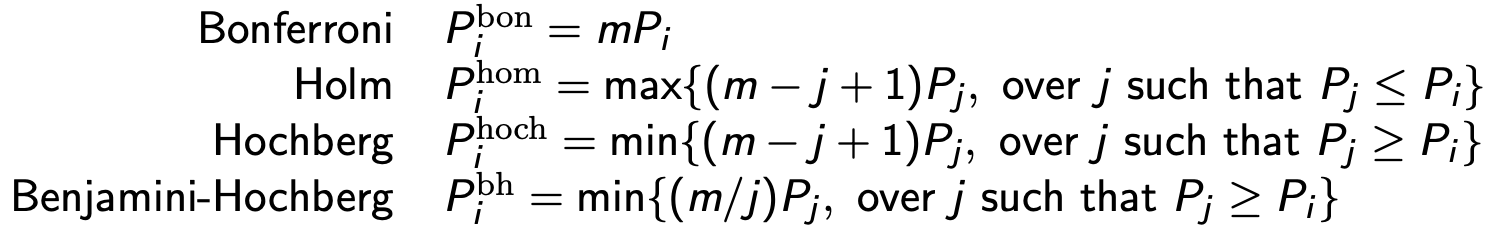
5. 통계적 검정의 종류 [목차]
⑴ 개요
② 단순 검정
⑵ 종류 1. one sample categorical
① 요약 통계량 : table
② 시각화 : bar chart (= bar plot), pie chart
③ 1-1. 카이제곱 단순적합도 검정
④ 1-2. 우도비 검정
⑤ 1-3. 런 검정
⑥ 1-4. 시뮬레이션 : Monte Carlo simulation (e.g., permutation)
⑶ 종류 2. multi sample categorical
① 요약 통계량 : contingency table
② 시각화 : segmented bar plot, side-by-side barplot
③ 2-1. 카이제곱 단순적합도 검정
④ 2-2. 카이제곱 독립성 검정
⑤ 2-3. Fisher's exact test (hypergeometric test)
⑥ 2-4. 시뮬레이션 : Monte Carlo simulation, parametric bootstrap
⑷ 종류 3. one sample numerical
① 요약 통계량 : location, scale
○ location : mean, median, quantile 등
○ scale : standard deviation, median absolute deviation 등
② 시각화 : boxplot, histogram, Q-Q plot (정규성 확인)
③ 3-1. T 검정
④ 3-2. 카이제곱 단순적합도 검정 : data binning 전략
⑤ 3-3. Kolmogorov-Smirnov 검정
⑥ 3-4. 시뮬레이션 : Monte Carlo simulation, nonparametric bootstrap, parametric bootstrap
⑸ 종류 4. two sample numerical
① 시각화 : side-by-side box plot, Q-Q plot (정규성 확인)
② 4-1. paired t-test : 단표본. parametric
③ 4-2. unpaired t-test with equal variance : 이표본. parametric
④ 4-3. unpaired t-test with unequal variance (Welch t-test) : 이표본. parametric
⑤ 4-4. Wilcoxon signed rank test : 단표본. non-parametric
⑥ 4-5. Wilcoxon rank-sum test : 이표본. non-parametric
⑦ 4-6. Kolmogorov-Smirnov two-sample test : 이표본. non-parametric
⑧ 4-7. 시뮬레이션 : Monte Carlo simulation (e.g., permutation), bootstrap
⑹ 종류 5. multiple sample numerical
① 시각화 : side-by-side box plot
② 5-1. one-way ANOVA : parametric
○ 가정 : iid, normality, homoscedasticity (단, Welch ANOVA F-test는 해당 없음)
○ 시각화 : residual plot (등분산성 확인), Q-Q plot (정규성 확인)
③ 5-2. Tukey's honest significant difference
○ 가정 : normality, homoscedasticity (단, Welch ANOVA F-test는 해당 없음)
④ 5-3. Kruskal-Wallis test : non-parametric
⑤ 5-4. Friedman test
⑥ 5-5. two-way ANOVA
○ 시각화 : side-by-side boxplot, residual plot (등분산성 확인), interaction plot
⑦ 5-6. permutation test
⑺ 종류 6. bivariate paired numerical
① 요약 통계량 : 상관계수
② 시각화 : scatter plot
③ 6-1. Pearson correlation
④ 6-2. Spearman correlation
⑤ 6-3. Kendall's tau correlation
⑥ 6-4. Cochran-Mantel-Haenszel (CMH) 검정
⑦ 6-5. Kolmogorov-Smirnov 독립 검정
⑧ 6-6. Monte Carlo simulation (e.g., permutation)
⑻ 종류 7. simple regression
① 시각화 : scatter plot
② 7-1. T 검정
③ 7-2. 시뮬레이션 : nonparametric bootstrap, parametric bootstrap
입력: 2019.06.19 14:52
수정: 2024.09.29 20:!6
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 3-1강. 포함배제의 원리 (0) | 2019.06.27 |
|---|---|
| 【통계학】 15강. 분산분석(ANOVA) (5) | 2019.06.21 |
| 【통계학】 13강. 통계적 추정 (0) | 2019.06.19 |
| 【통계학】 11강. 표본집단과 표본분포 (0) | 2019.06.19 |
| 【통계학】 8강. 확률변수변환 (0) | 2019.06.19 |





최근댓글