14-10강. Cochran-Mantel-Haenszel (CMH) 검정
추천글 : 【통계학】 14강. 통계적 검정
1. 개요 [본문]
2. 유도 [본문]
3. 해석 [본문]
1. 개요 [목차]
⑴ 정의 : 두 변수 X와 Y 사이의 관계를 제3 변수로 계층화한 경우 더 잘 설명되는지를 통계적으로 검정하는 방법
⑵ 귀무가설 H0 : 계층이 주어져 있을 때 X와 Y의 상관관계가 계층이 주어지지 않았을 때와 차이가 나지 않음 (조건부 독립)
⑶ 예를 들어, 치료와 반응 사이의 상관관계를 나이에 따라 계층적으로 구분하여 설명하는 게 더 유의한지를 검정할 수 있음
⑷ 계층(stratum)은 범주형 데이터를 원칙으로 하며, 연속형 데이터도 구간화하면 적용할 수 있음
2. 유도 [목차]
⑴ (X, Y)가 N개의 순서쌍 관측데이터로 존재한다고 가정
⑵ 관측데이터를 제3의 변수(예 : 나이)에 의해 K개의 계층으로 구분된다고 가정 : 각 계층의 관측데이터 개수를 Nk로 정의

⑶ k번째 계층의 확률변수를 (Xk, Yk)로 정의하고, 해당 계층에 속하는 데이터를 (x1k, y1k), ···, (xNk, yNk)와 같이 표시
⑷ Tk를 다음과 같이 정의

⑸ CMH 통계량을 다음과 같이 정의

⑹ ρs의 분산 : 통계적 구간추정에 활용할 수 있음
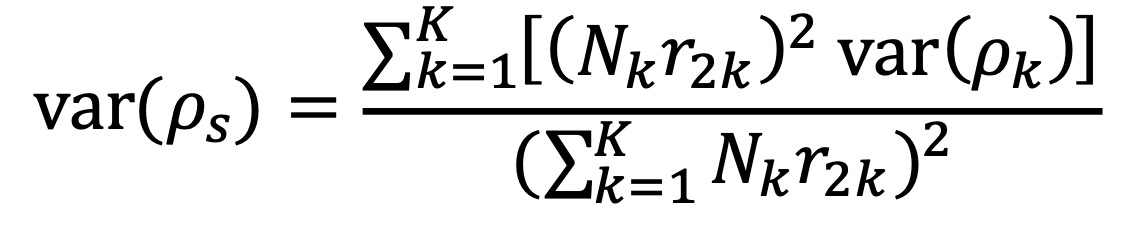
3. 해석 [목차]
⑴ CMH 통계량 혹은 M2
① M2이 충분히 커서 p-value가 낮다면 계층(stratum)에 따라 두 변수 사이의 상관관계가 다르게 나타남을 나타냄
② M2 통계량 자체는 변수 간 가중치 상관관계뿐만 아니라 샘플의 크기에 의존함
③ 예를 들어, 계층화가 전혀 없다면 M2 = ρ2 (N-1) (단, ρ는 전체 Pearson 상관계수)
⑵ SCC(stratum-adjusted correlation coefficient) 혹은 ρs
① 계층화를 고려한 두 변수 간 가중치 상관계수로 M2 대신 ρs를 이용함
⑶ -1 ≤ ρs ≤ 1
① ρs = 1 : 완전 양의 상관(perfect positive correlation)
② ρs = -1 : 완전 음의 상관(perfect negative correlation)
③ ρs = 0 : 상관관계 없음(no correlation)
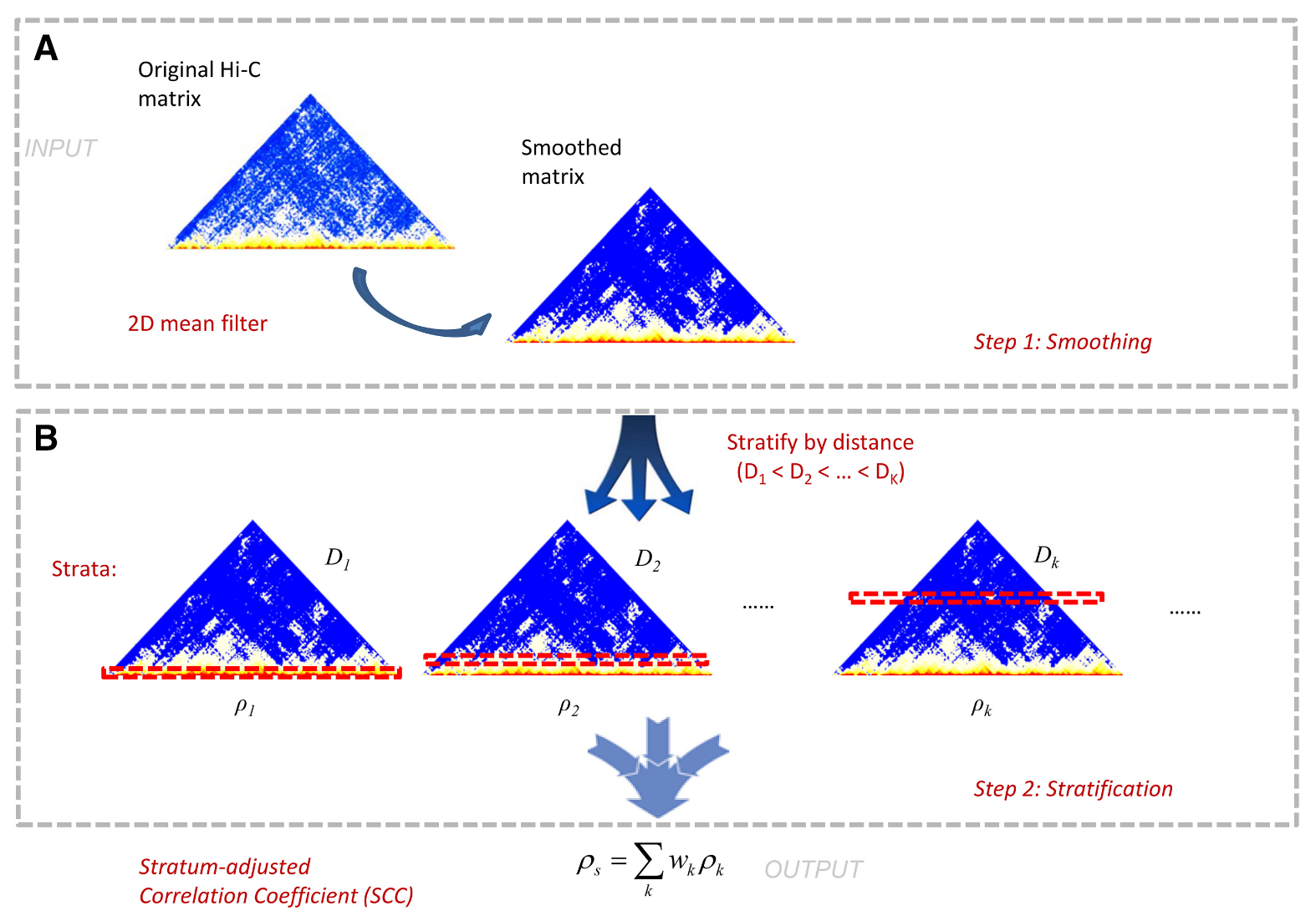
⑷ 응용. HiCRep : 한 쌍의 Hi-C 생물정보학 데이터 간 유사도를 평가할 때, contact matrix의 상관계수의 거리별 의존성을 확인
Figure. 1. HicRep
입력: 2024.10.13 23:27
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 통계학 기초 문제 [21-40] (2) | 2024.12.25 |
|---|---|
| 【통계학】 통계학 기초 문제 [01-20] (5) | 2024.12.24 |
| 【통계학】 18강. 회귀분석의 정규화 (2) | 2024.10.10 |
| 【통계학】 21강. 정보이론 (5) | 2024.10.07 |
| 【통계학】 14-4강. 우도비 검정과 Wilks’ phenomenon 증명 (3) | 2024.09.25 |




최근댓글