21강. 정보이론(information theory)
추천글 : 【통계학】 통계학 목차
1. 정보이론 [본문]
2. 변분추론 [본문]
3. 현대 정보이론 [본문]
1. 정보이론 [목차]
⑴ 개요
① low probability event : high information (surprising)
② high probability event : low information (unsurprising)
⑵ entropy
① 문제 상황 : X는 Raining / Not Raining. Y는 Cloudy / Not Cloudy
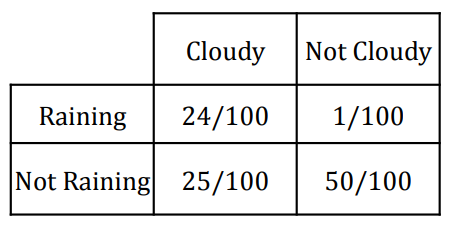
Figure. 1. 엔트로피 예제
② 통계학 기본 개념

③ 정보(information, information content), uncertainty(surprisal, unexpectedness, randomness)
○ 정의 : 수학적 불확실성을 측정하는 양
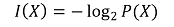
○ 밑이 2인 log2인 경우 : bits라는 단위를 사용
○ 밑이 e인 자연로그인 경우 : nats라는 단위를 사용
○ 특징 1. p(xi) = 1이라면 I(xi) = 0
○ 특징 2. I(xi) ≥ 0
○ 특징 3. P(x = xi) < P(x = xj)라면 I(xi) > I(xj)
○ 특징 4. xi와 xj가 독립이라면, I(xixj) = I(xi) + I(xj)
④ entropy (self information, Shannon entropy)
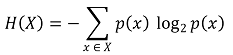
○ 이해 : 특정 매체로부터 얻어지는 정보
○ 즉, entropy는 uncertainty의 평균값으로 정의됨
○ 물리학에서의 엔트로피처럼 무질서할수록 높은 값이 나옴 : 엔트로피가 높으면 heterogeneity가 높음을 의미
○ 각 사건의 surprisal(-log p(x))에 각 사건에 대한 확률 가중치(p(x))를 적용한 것
○ redundancy : 최대 엔트로피 - 실제 엔트로피
○ 예시
○ fair coin toss : H = -0.5 log2 0.5 - 0.5 log2 0.5 = 1
○ fair die : H = 6 × (-(1/6) log2 (1/6)) = log2 6 = 2.58
○ X가 균일분포를 따른다면, H(X) = log n이 성립함
○ 소스 코딩 정리(source coding theorem)
○ 정의 : 매우 긴 데이터 시퀀스에 대해 압축률을 최대로 끌어올릴 경우, 압축된 데이터의 평균 비트 수가 엔트로피에 근접
○ 즉, 주어진 경우의 수를 표현하기 위해 필요한 비트 수
○ log2로 저장되는 경우 비트 수를 나타내는 것이고, logk로 저장되는 경우 k-ary system에서 필요한 저장 용량 크기
○ Kraft 부등식 : 모든 entity를 고유한 비트 시퀀스로 표현할 수 있도록 보장하는 제한 조건
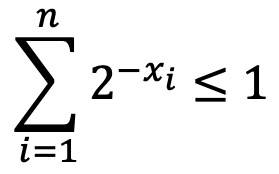
○ 소스 코딩 정리 증명 : 평균 비트 수 p1x1 + ··· + pnxn에 대하여, 라그랑주 승수법을 적용
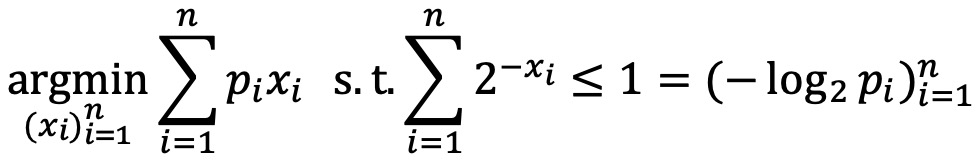
○ 특징 1. H(X)는 shift-invariant
○ Y = X + a일 때, pY(y) = pX(x)이므로 H(Y) = H(X)가 성립
○ 특징 2. H(X) ≥ 0
○ 특징 3. Hb(X) = (logba) Ha(X) (단, a, b는 로그의 밑)
○ logbp = (logba) logap
○ 응용 : ID3, C4.5, C5 등에서 쓰임
○ 파이썬 코드
import numpy as np
def shannon_index(data):
# 데이터에서 고유 값과 각 값의 개수를 세기
values, counts = np.unique(data, return_counts=True)
# 개수를 사용하여 비율 계산
proportions = counts / sum(counts)
# 비율이 0이 아닌 경우에 대해 Shannon index 계산
return -np.sum(proportions * np.log(proportions))
# 예제 데이터, 여기서 1이 3개, 2가 2개, 3이 1개 있음
data = [1, 1, 1, 2, 2, 3]
# Shannon index 계산
index = shannon_index(data)
print(f"Shannon index: {index}")
⑤ joint entropy
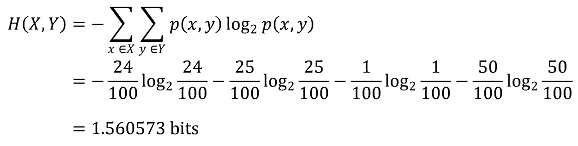
○ 특징 1. H(X, Y) ≤ H(X) + H(Y) : X와 Y가 독립이라면 H(X, Y) = H(X) + H(Y)
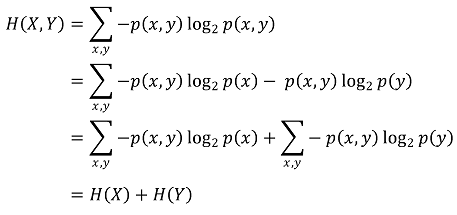
⑥ 조건부 엔트로피(conditional entropy)
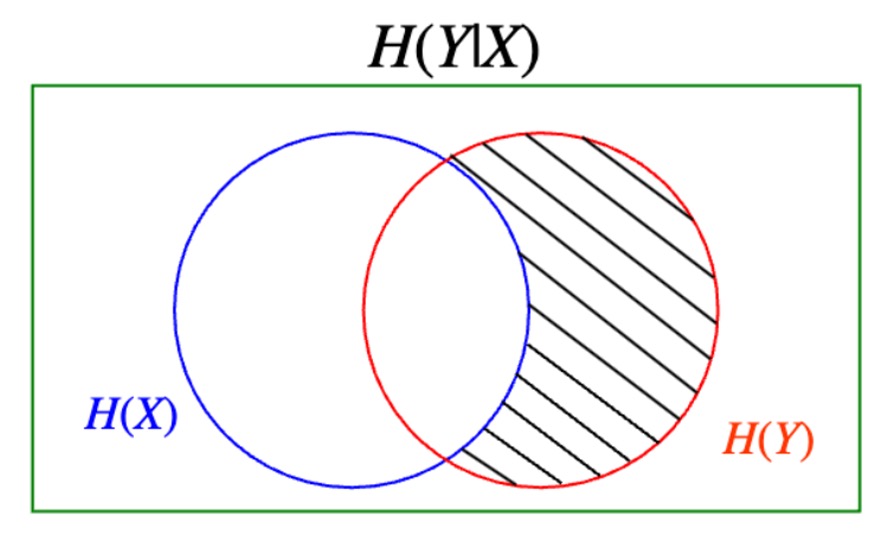
Figure. 2. 조건부 엔트로피 시각화
○ 특정 조건에 대한 조건부 엔트로피
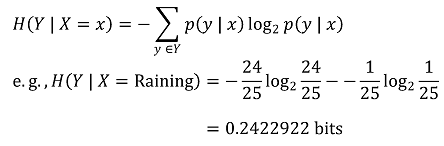
○ 전체 조건부 엔트로피
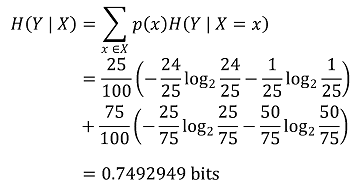
○ 정보 이득(IG, information gain) : X라는 정보를 앎으로써 무질서한 상황이 질서 있게 바뀐 경우 정보 이득이 큼
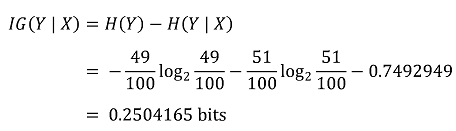
○ information bottleneck method (IB) : 정보이론을 이용하여 복잡도와 정확도 간 트레이드오프를 기술
○ 응용 : 가령, 주어진 데이터에서 클러스터의 개수를 몇 개로 할 것인지를 알려줄 수 있음
○ 특징 1. X와 Y가 독립이라면 H(Y | X) = H(Y) (cf. H(Y | X) ≤ H(Y))
○ 특징 2. H(Y | Y) = 0
○ 특징 3. H(X, Y) = H(X) + H(Y | X) = H(Y) + H(X | Y) (연쇄법칙(chain rule))
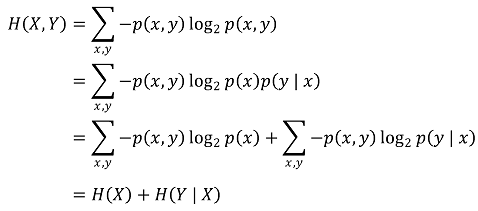
○ 특징 4. H(X, Y | Z) = H(X | Z) + H(Y | X, Z)
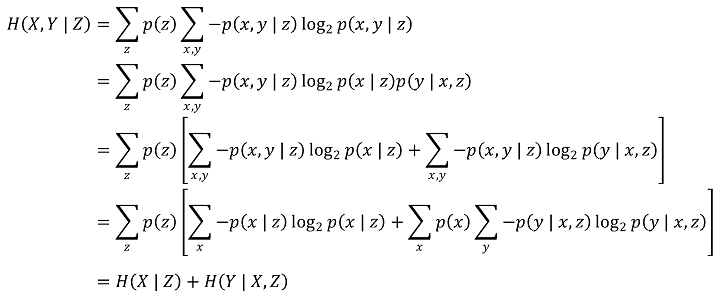
⑦ mutual information
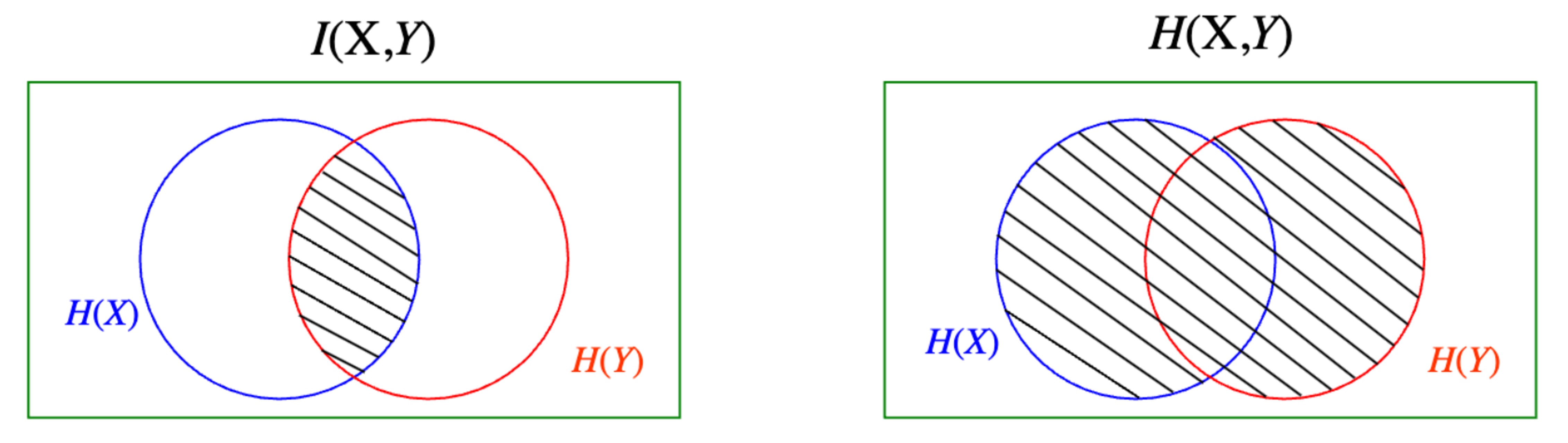
Figure. 3. mutual information 시각화
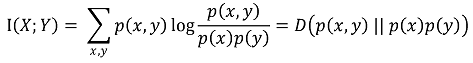
○ 정보 이득과 mutual information은 동일함
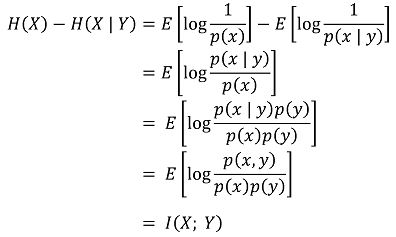
○ 특징 1. I(X; Y) = H(Y) - H(Y | X) = H(X) - H(X | Y)
○ 특징 2. mutual information ≥ 0 (등호조건 : X와 Y가 독립)
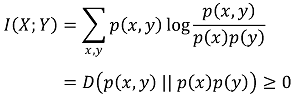
○ 특징 3. H(X | Y) ≤ H(X) (등호조건 : X와 Y가 독립) : 조건은 엔트로피를 감소시킨다는 의미
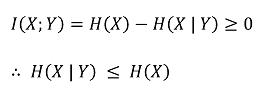
○ 특징 4. I(X; Y) ≤ H(X, Y) : H(X, Y) - I(X; Y)는 수학적 거리의 정의를 만족함
○ 응용 1. mutual information은 이미지 간 유사도 판단 시 사용할 수 있음
○ 응용 2. mRMR(maximum relevance minimum redundancy) : output과 mutual information이 높으면서 상호 간 mutual information이 낮은 피처들을 고르는 기법. 머신러닝에서 자주 사용. 매트랩 코드는 다음과 같음
% Rank features using mRMR
selected_features_idx = fscmrmr(features, labels);
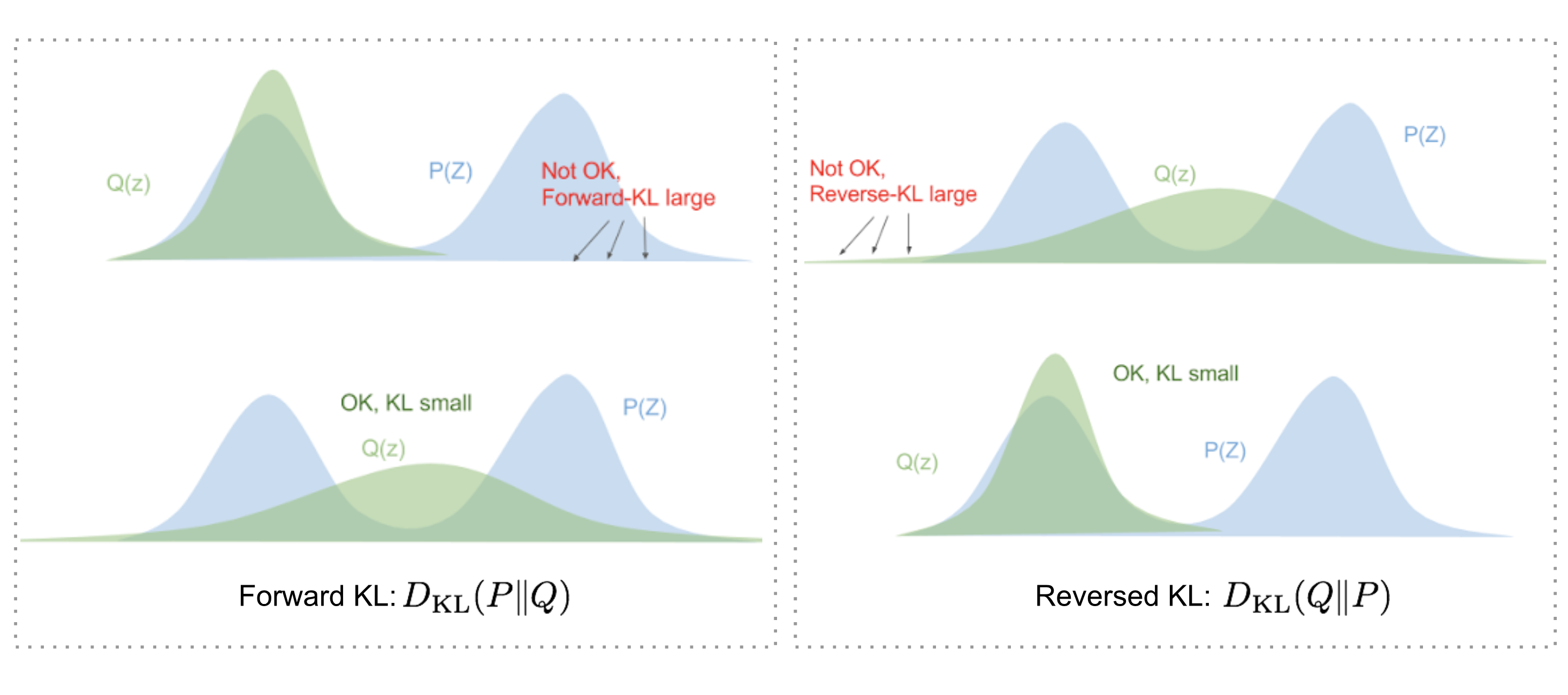
⑧ 상대 엔트로피(relative entropy, Kullback Leibler divergence, KL divergence, KLD)
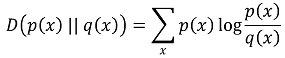
○ 개요
○ 두 개의 확률분포가 얼마나 발산하는지를 나타내는 척도
○ true distribution을 모방하는 approximate distribution p(x)가 앞에 오고, true distribution q(x)가 뒤에 옴
○ 일반적으로 true distribution은 복잡한 분포 함수이고, approximate distribution은 parameter model
○ approximate distribution은 manageble하므로, 정규분포처럼 단순한 분포로 할 수 있음
○ 엄밀하게는 수학적 거리의 정의를 충족하지 않음
○ 특징 1. asymmetry : DKL(p(x) || q(x)) ≠ DKL(q(x) || p(x)) (∴ 수학적 거리의 정의를 위배함)
Figure. 4. DKL(p || q)와 DKL(q || p)의 차이
○ 특징 2. D(p || q) ≥ 0 (등호조건 : p(x) = q(x))
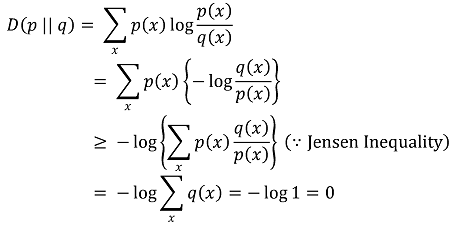
○ 특징 3. H(X) ≤ log n (단, n은 X가 취할 수 있는 원소의 개수)
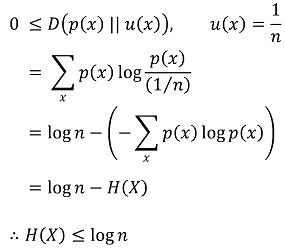
○ 응용 : 알려지지 않은 진실한 데이터 분포 q와 가장 KL divergence가 작은 예측 데이터 분포 p를 결정하는 문제
○ log-likelihood를 극대화하면 KL divergence를 최소화할 수 있음
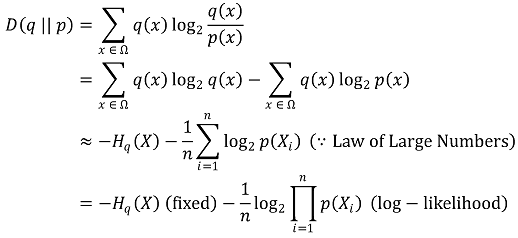
○ 응용 : Jensen-Shannon divergence (JSD)
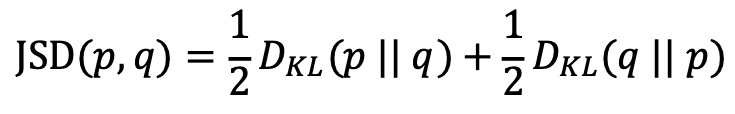
⑨ 크로스 엔트로피(cross entropy)
○ 정의 : 두 확률분포 p와 q를 구분하기 위해 필요한 평균 비트 수
○ 머신러닝에서는 일반적으로 surprisal에 model prediction을, 사건의 가중치에 true distribution을 적용함

○ 특징 1. -∑ pi log qi = H(p) + DKL(p || q)
○ 특징 2. DKL(p || q)를 최소화하는 것은 cross-entropy를 최소화하는 것과 동일함 : H(p)가 상수이기 때문
○ 특징 3. -∑ pi log qi를 최소화할 때 pi가 uniform distribution이라고 가정하는 경우를 최대우도추정이라고 함
⑩ AEP(asymptotic equipartition property)
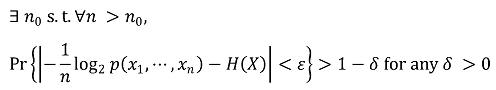
⑶ 비교 1. Rényi entropy
① (참고) Hartley (max) entropy : M개의 심볼로 표현되는 소스에 대해 (예 : 알파벳으로 표현되면 M = 26)
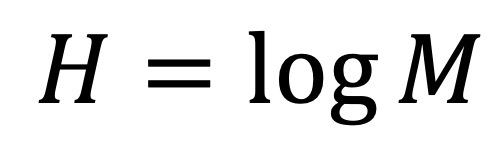
② (참고) min entropy : 신호 처리와 관련됨. 다른 모든 기호에 비해 특정 기호가 발생할 가능성이 더 높을 때 사용
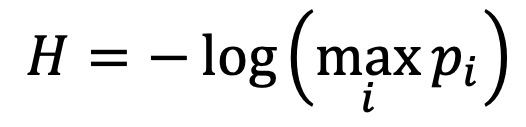
③ Rényi entropy : Shannon entropy (α → 1; 로피탈 정리), max entropy (α → 0), min entropy (α → ∞)를 모두 포괄
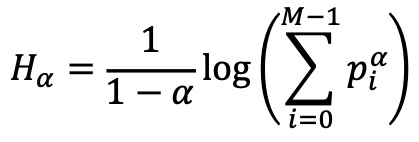
④ Rényi divergence : α → ∞이면 Rényi divergence는 KL divergence로 수렴 (∵ 로피탈 정리)
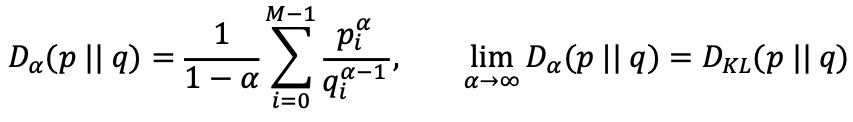
⑷ 비교 2. sample entropy
① 시간을 반영한 dynamic measure
② 신호 처리에서 중요함
⑸ 비교 3. Gini impurity
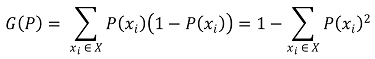
① entropy가 유일무이한 척도는 아니므로 Gini impurity와 같은 대안적인 척도가 제시됨
② Gini impurity는 잘못 레이블링할 확률(1 - P(xi))에 각 샘플에 대한 가중치(P(xi))를 고려한 것
③ Gini impurity와 entropy 모두 주어진 데이터가 무질서할수록 높은 값을 보임 : impurity의 어원
④ 응용 : CART((simple) classification and regression tree)에서 쓰임
⑤ (구별 개념) 경제학에서의 지니계수
○ 소득의 불평등을 평가하기 위해 처음으로 도입된 개념 : 소득뿐만 아니라 변량의 분포의 불평등도도 비슷하게 평가할 수 있음
○ 지니계수가 경제학에서 머신러닝 및 정보이론 분야로 넘어가면서 비슷한 불평등도를 암시하나 수학적 정의가 달라짐
○ 차이 : 변량의 분포가 모두 동일하면,
○ 경제학에서의 지니계수 : 극단적으로 평등해지므로 경제학에서의 지니계수는 0의 값을 가짐
○ 정보이론에서의 지니계수 : 코시-슈바르츠 부등식에 의해 최댓값을 가짐. 직관적으로는 가장 무질서해지므로 최댓값
⑹ 비교 4. connectivity index (CI)
① 공간전사체 상에서, 특정 스팟과 가장 유사한 스팟(nearest neighbor)이 서로 다른 클러스터에 있으면 CI 값이 높아짐 (ref)
② 따라서 CI 값이 높을수록 heterogeneity가 높음을 암시함
⑺ 비교 5. Simpson index
① Shannon entropy와 함께, 정보이론에 기반한 또다른 척도
② 공간전사체 기준으로, 두 개의 랜덤한 스팟이 동일한 클러스터에 속할 확률 (ref)
③ Simpson index가 낮을수록 heterogeneity가 높음을 암시함
⑻ 비교 6. cluster modularity
① 공간전사체 기준으로, 클러스터 내 스팟의 purity (homogeneity)를 나타내는 메트릭 (ref)
⑼ 비교 7. Lempel-Ziv complexity
⑽ 비교 8. Silhouette coefficient
⑾ 비교 9. Calinski-Harabasz index
2. 변분추론 [목차]
⑴ 개요
① A가 관찰시 B가 원인이었을 확률 P(B | A)를 사후확률(posterior)이라고 함 (cf. Bayes' theorem)
② 변분추론(variational inference) : 복잡한 사후 분포를 추론하기 위해 좀 더 단순한 변분분포(variational distribution)를 도입하고, 이 둘 간의 차이를 줄이는 방향으로 추론을 하는 것
⑵ ELBO(evidence lower bound) : 변분추론의 표준 방법
① (참고) 젠센부등식(Jensen's inequality) : log 함수와 같이 위로 볼록한 함수(오목함수, concave function)은 다음이 성립함
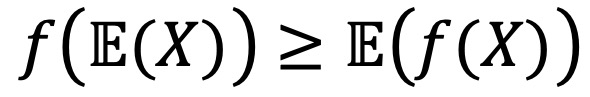
② 문제 상황 : 주어진 데이터 x에 대한 증거 p(x), 은닉 변수 z에 대하여, 다음과 같은 모델의 log evidence를 직접 계산하기 어려움
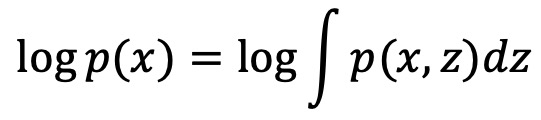
③ 수식화
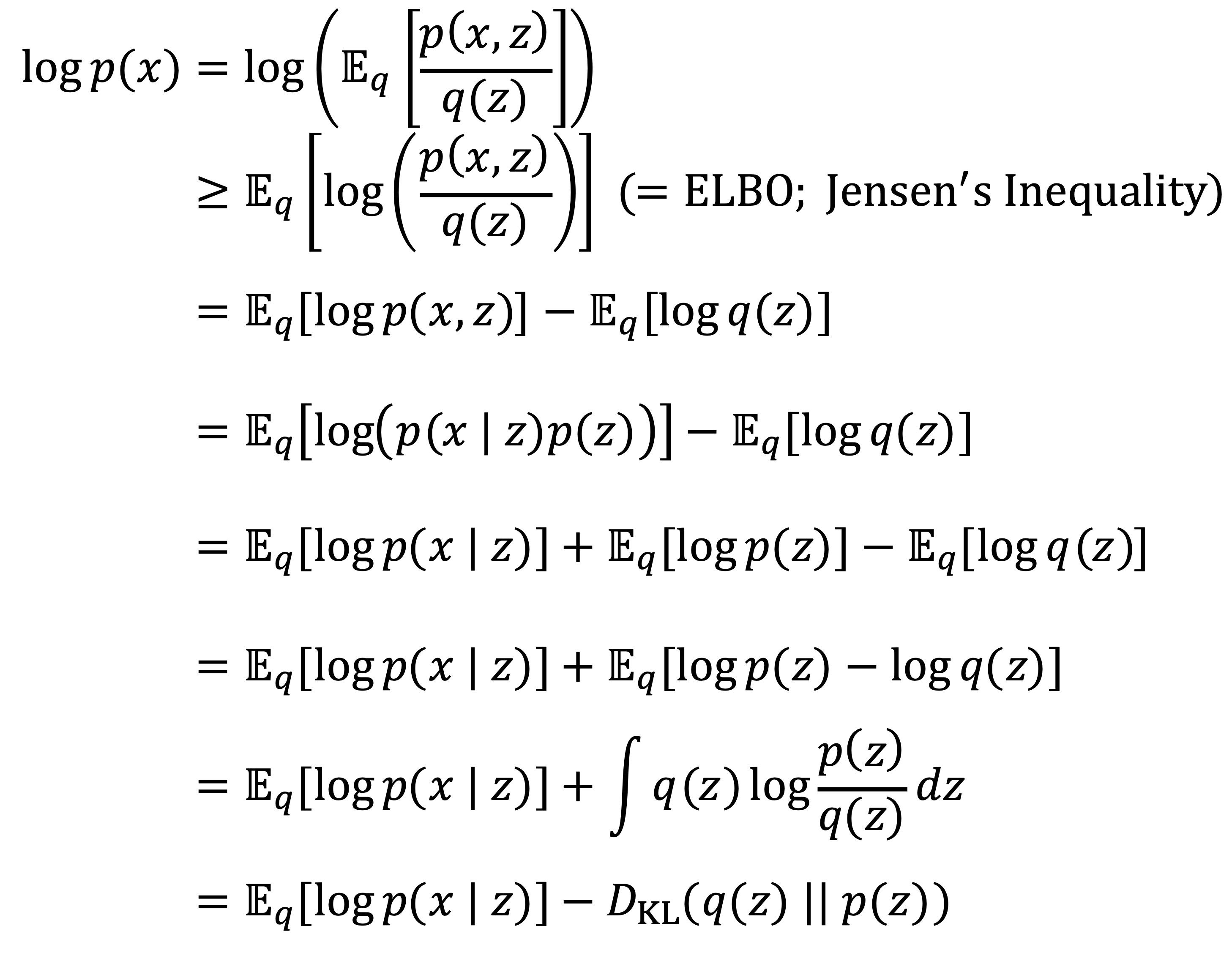
○ ELBO = 𝔼q(z) [log p(x, z)] - 𝔼q(z) [log q(z)]
○ 변분 추론에서는 ELBO를 최대화하면 log p(x)는 상수이므로 위 부등식의 등호조건 성립에 가까워짐
○ log (p(x, z) / q(z))가 직선함수가 된다는 식으로 단순히 해석하기보다는 p(x, z) / q(z)가 z에 대해 상수가 된다는 게 더 정확함
○ p(x, z) / q(z) = z에 대하여 상수 ⇔ q(z) ∝ p(x, z) ⇔ q(z) = q(z | x) = p(x, z) / p(x) = p(z | x)
○ 결론 : ELBO를 최대화하면 변분분포 q(z | x)가 진정한 사후분포 p(z | x)와 가까워짐
④ 예 1
⑤ 예 2. 가변인코더(VAE)와 그래프 가변인코더(GVAE)의 손실함수
3. 현대 정보이론 [목차]
⑴ 연혁
① Ludwig Boltzmann (1872) : 기체 입자의 엔트로피를 설명하기 위해 H-theorem을 제안
② Harry Nyquist (1924) : "지능"과 이것이 통신 체계로 전파되는 속도를 정량화
③ John von Neumann (1927) : 깁스 자유 에너지를 양자역학으로 확장
④ Ralph Hartley (1928) : 수신자의 구별 가능한 정보의 개수를 로그를 이용하여 표현
⑤ Alan Turing (1940) : 독일 에니그마 암호를 해독하기 위해 deciban을 소개
⑥ Richard W. Hamming (1947) : Hamming code를 개발
⑦ Claude E. Shannon (1948) : 정보이론을 주창. A Mathematical Theory of Communication
⑧ Solomon Kullback & Richard Leibler (1951) : Kullback-Leibler divergence를 소개
⑨ David A. Huffman (1951) : Huffman encoding을 개발
⑩ Alexis Hocquenghem & Raj Chandra Bose & Dwijendra Kumar Ray-Chaudhuri (1960) : BCH code를 개발
⑪ Irving S. Reed & Gustave Solomon (1960) : Reed-Solomon code를 개발
⑫ Robert G. Gallager (1962) : low-density parity check를 소개
⑬ Kolmogorov (1963) : Kolmogorov complexity (minimum description length)를 소개
⑭ Abraham Lempel & Jacob Ziv (1977) : Lempel-Ziv 압축 (LZ77)을 개발
⑮ Claude Berrou & Alain Glavieux & Punya Thitimajshima (1993) : Turbo code를 개발
⑯ Erdal Arıkan (2008) : polar code를 소개
⑵ 종류 1. 암호(encoding)
① Huffman code
② Shannon code
③ Shannon-Fano-Elias code (alphabetic code)
⑶ 종류 2. 압축(compression)
① UD(uniquely decodable)
② Kraft inequality
⑷ 종류 3. network information theory
⑸ 종류 4. quantum information theory
입력: 2021.11.10 22:28
수정: 2023.03.21 16:22
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 14-10강. Cochran-Mantel-Haenszel (CMH) 검정 (7) | 2024.10.14 |
|---|---|
| 【통계학】 18강. 회귀분석의 정규화 (2) | 2024.10.10 |
| 【통계학】 14-4강. 우도비 검정과 Wilks’ phenomenon 증명 (3) | 2024.09.25 |
| 【통계학】 Optimal Transport 및 Gromov-Wasserstein 거리 이해하기 (3) | 2023.11.04 |
| 【통계학】 5-2강. 거리함수와 유사도 (2) | 2023.10.24 |




최근댓글