9강. 통계학 주요 정리 1부
추천글 : 【통계학】 통계학 목차
1. 마르코프 부등식 [본문]
2. 체비셰프 부등식 [본문]
3. 칸텔리 부등식 [본문]
4. 코시-슈바르츠 부등식 [본문]
5. 젠센 부등식 [본문]
6. 큰 수의 법칙 [본문]
7. 중심극한정리 [본문]
8. Slutsky's theorem [본문]
9. Laplace's rule of succession [본문]
a. 대중의 지혜
1. 마르코프 부등식(Markov inequality) [목차]
⑴ 정리
X가 확률변수이고 a ＞ 0일 때, 다음이 성립한다.
⑵ 증명 1.
확률변수 X를 이루는 이벤트를 x1, ···, xn이라고 하자.
위 이벤트들을 재정렬하여 | xi | ≥ a ⇔ i = r+1, ···, n이 되도록 하자.
⑶ 증명 2.
2. 체비셰프 부등식(Chebyshev inequality) [목차]
⑴ 정리
기댓값이 m이고 분산이 σ2인 확률변수 X가 있다고 하자. 단, 이때 분산은 유한한 값이다. 그러면 어떠한 실수 k ＞ 0에 대해서도 다음 부등식이 성립한다.
단, k ＞ 1인 경우에만 의미 있는 정보를 제공한다.
⑵ 증명 1.
확률변수 X를 이루는 이벤트를 x1, ···, xn이라고 하자.
위 이벤트들을 재정렬하여 | xi - m | ≥ kσ ⇔ i = r+1, ···, n이 되도록 하자.
⑶ 증명 2.
마르코프 부등식에서 k = 2, ε = kσ, X → X - μX인 경우가 체비셰프 부등식이다.
3. 칸텔리 부등식(Cantelli inequality, one-tailed chebyshev inequality) [목차]
⑴ 정리
기댓값이 m이고 분산이 σ2인 확률변수 X가 있다고 하자. 단, 이때 분산은 유한한 값이다. 그러면 어떠한 실수 k ＞ 0에 대해서도 다음 부등식이 성립한다.
⑵ 증명
① m = 0일 때
확률변수 X를 이루는 이벤트를 x1, ···, xn이라고 하자.
위 이벤트들을 재정렬하여 xi ＜ kσ ⇔ i = r+1, ···, n가 되도록 하자.
kσ = t라고 두면,
② m = μ ≠ 0일 때
X' = X - μ는 기댓값이 0이고 분산이 σ2인 확률변수이다.
따라서 다음이 성립한다.
4. 코시-슈바르츠 부등식(Cauchy-Schwartz inequality) [목차]
⑴ 정리
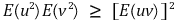
⑵ 증명
⑶ 예제
① E(1 / X) ≥ 1 / E(X)
② ln (E(X)) ≥ E(ln X)
5. 젠센 부등식(Jensen's inequality) [목차]
⑴ (참고) 볼록함수와 오목함수
① 볼록집합(convex set) : 집합 내 임의의 두 점을 양끝으로 하는 선분의 모든 점이 항상 해당 집합의 원소인 경우
② 볼록함수(convex function) :｛(x, y) | y ≥ f(x)｝가 볼록집합인 함수. 아래로 볼록과 유사
③ 강볼록함수(strictly convex function)
④ 오목함수(concave function) :｛(x, y) | y ≤ f(x)｝가 볼록집합인 함수. 위로 볼록과 유사
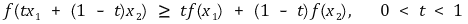
⑤ 강오목함수(strictly concave function)
⑥ 선형함수(linear function) : 볼록함수이자 오목함수
⑵ 볼록성과 이차도함수의 관계 : f"(x) ≥ 0인 것과 볼록함수인 것은 필요충분이고, f"(x) ≤ 0인 것과 오목함수인 것은 필요충분
① 증명 1.
② 증명 2. 볼록함수의 경우 f"(x) ≥ 0이고 오목함수의 경우 f"(x) ≤ 0이 성립함을 보이는 쉬운 증명
⑶ 젠센부등식 : 차원의 확장
① f가 볼록함수인 경우 다음 부등식이 성립함
② f가 오목함수인 경우 다음 부등식이 성립함
③ 증명 1. 수학적 귀납법
④ 증명 2. 직선함수의 도입
○ 증명
ℓ(x)를 (E(X), f(E(X)))를 지나고 f(x)에 접하는 직선함수라고 정의하자.
f가 볼록함수라고 하자.
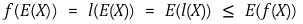
⑷ 경제통계적 의미
① 위험애호
○ 볼록함수
○ 평균에 대한 효용함수가 더 작은 경우
○ 모험을 더 선호하는 경우
② 위험기피
○ 오목함수
○ 평균에 대한 효용함수가 더 큰 경우
○ 예측 가능한 결과를 더 선호하는 경우
③ 위험중립
6. 큰 수의 법칙(LLN, law of large numbers) : 대수의 법칙이라고도 함 [목차]
⑴ 정리
임의의 실수 α ＞ 0에 대하여 다음 식이 성립한다.
⑵ 증명
확률변수 X의 평균을 m, 표준편차를 σ라고 하자.
임의의 실수 k ＞ 0에 대해, 체비셰프 부등식을 적용하자.
⑶ 충분조건
① Xi, i = 1, ···, n은 i.i.d
② VAR(Xi) ＜ ∞
7. 중심극한정리(CLT, central limit theorem) [목차]
⑴ 개요
① 정의 : 표본수가 무한히 크면 표본의 분포와 관련 없이 표본합 또는 표본평균은 정규분포를 따름
② 수학적 표현 : 분포수렴(convergence in distribution)을 이용
⑵ 증명 1.
사건이 일어날 확률을 p라고 하면, n번의 시행 중 사건이 k번 일어날 확률은 다음과 같다.
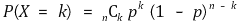
n이 무한대에 다가갈수록 이 확률분포는 거의 연속적으로 변한다. 따라서 실수를 정의역으로 하는, 다음과 같은 함수 f(x)를 생각할 수 있다.
① 평균
이 분포상의 x = m에서 f가 극댓값을 가지게 된다면, 다음의 식을 만족한다.
다음을 주목하자.
단, n!의 정의는 다음과 같음을 스털링 근사로 엄밀히 증명 가능하다.
그러므로
② 이항분포의 정규근사
충분히 작은 Δx = x - m에 대해 다음이 성립한다.
따라서 B(n, p)는 평균과 가까운 구간에 대해서 N(np, npq)와 근사하다. (단, n ≫ 1)
⑶ 증명 2. m(t)의 도입과 적률생성함수
⑷ 충분조건
① Xi, i = 1, ···, n은 i.i.d
② 0 ＜ VAR(Xi) ＜ ∞
8. Slutsky's theorem [목차]
⑴ (참고) 확률수렴(convergence in probability) : 확률변수 S1, S2, ···, Sn, ···에 대해,
⑵ (참고) 분포수렴(convergence in distribution) : 확률변수 S1, S2, ···, Sn, ···과, 각각의 분포함수 F1, F2, ···, Fn과, 그리고 F가 분포함수인 S에 대해,
⑶ Slutsky's theorem 또는 확률극한법칙(algebra of probability limit) : p lim Xn, p lim Yn이 존재할 때,
① 6번 공식을 CMT(continuous mapping theorem)라고 함
9. Laplace's rule of succession [목차]
⑴ 정의 : n번의 시행 중 k번의 positive 결과가 나왔을 때, n+1번째의 시행에서 positive 결과가 나올 확률은 다음과 같음
⑵ 증명 (ref)
입력: 2019.05.03 15:02
'▶ 자연과학 > ▷ 통계학' 카테고리의 다른 글
| 【통계학】 8강. 확률변수변환 (0) | 2019.06.19 |
|---|---|
| 【통계학】 10강. 통계학 주요 정리 2부 (0) | 2019.06.18 |
| 【통계학】 7강. 연속확률분포 (0) | 2019.06.16 |
| 【통계학】 6강. 이산확률분포 (0) | 2019.06.16 |
| 【통계학】 5강. 통계량 (0) | 2019.06.16 |
최근댓글