7강. 연속확률분포
추천글 : 【통계학】 통계학 목차
1. 균일분포 [본문]
2. 정규분포 [본문]
3. 감마분포 [본문]
4. 지수분포 [본문]
5. 베타분포 [본문]
6. 파레토 분포 [본문]
7. 로지스틱 분포 [본문]
8. 디리클레 분포 [본문]
9. Gumbel 모델 [본문]
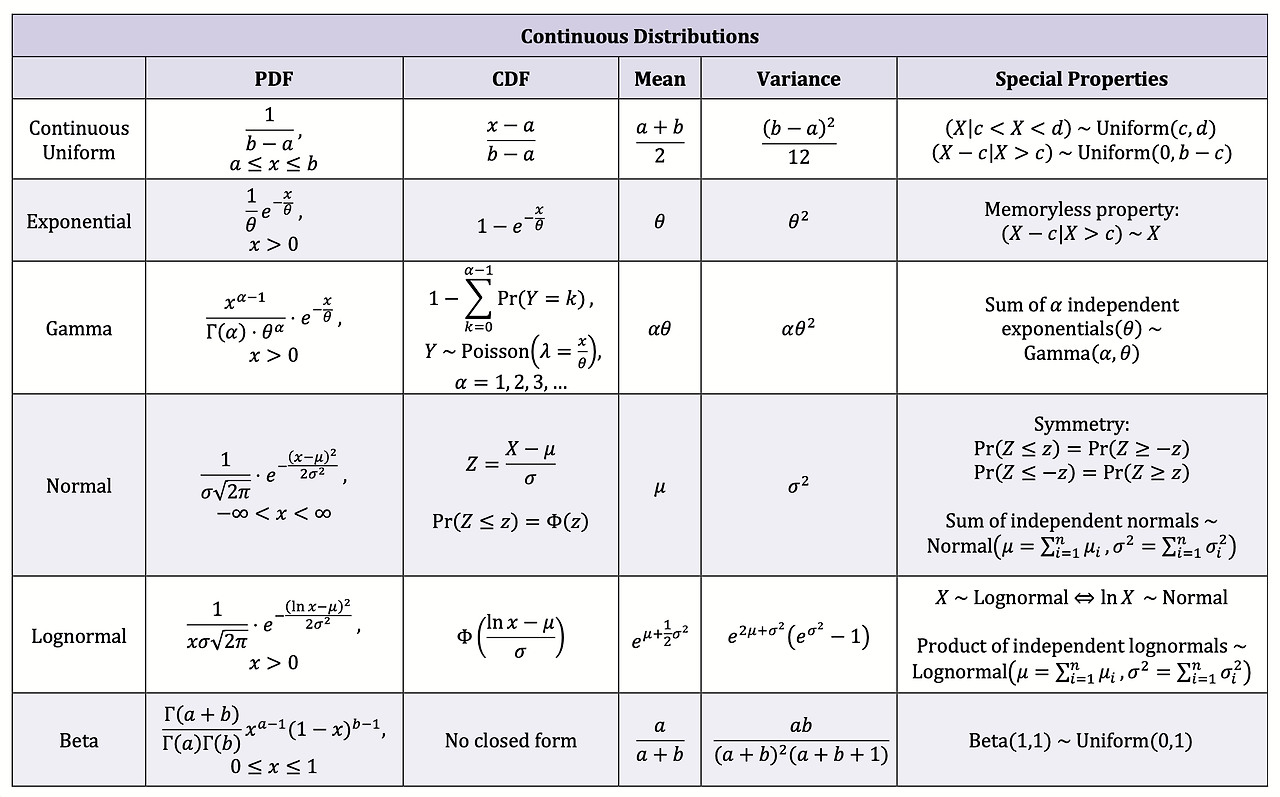
Table. 1. 연속확률분포
1. 균일분포(uniform distribution) [목차]
⑴ 정의 : 모든 확률변수에 대해 일정한 확률을 가지는 확률분포
⑵ 확률밀도함수 : X ~ u[a, b], p(x) = 1 / (b - a) I｛a ≤ x ≤ b｝
Figure. 1. X ~ u[1, 9]의 x-p(x) 그래프
① (참고) 파이썬 프로그래밍 (Bokeh)
from bokeh.plotting import figure, output_file, show
output_file("uniform_distribution.html")
p = figure(width=400, height=400, title = "Uniform Distribution",
tooltips=[("x", "$x"), ("y", "$y")])
p.line([1, 2, 3, 4, 5, 6, 7, 8, 9], [1/8, 1/8, 1/8, 1/8, 1/8, 1/8, 1/8, 1/8, 1/8],
line_width=2)
show(p)
⑶ 통계량
① 적률생성함수
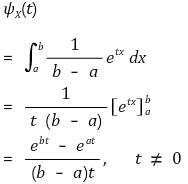
② 평균 : E(X) = (a + b) / 2
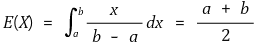
③ 분산 : VAR(X) = (b - a)2 / 12
④ 주변확률분포는 길이 ÷ 전체 면적의 의미를 가짐
⑷ 예제
① 균일분포 예제
2. 정규분포(normal distribution) [목차]
⑴ 정의 : nCx θx (1 - θ)n-x에서 n → ∞으로 극한을 취한 것
① 보편적으로 관찰되므로 정규분포라고 함
② 일반적으로 표준정규분포 밀도함수를 φ(·)로, 누적분포함수를 Φ(·)로 표시
③ 중심극한정리(central limit theorem) : X = ∑Xi인 경우 n → ∞으로 극한을 취하면 정규분포를 따름
④ 이항분포를 근사하기 위해 최초로 유도됨 (De Moivre, 1721)
⑤ 천문학에서 model error를 모델링하기 위해 사용됨 (Gauss, 1809)
○ 이로 인해 가우스분포(Gaussian distribution)라고도 함
⑵ 확률밀도함수
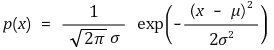
Figure. 2. 표준정규분포의 확률밀도함수
① (참고) 파이썬 프로그래밍 (Bokeh)
# see https://stackoverflow.com/questions/10138085/how-to-plot-normal-distribution
import numpy as np
import scipy.stats as stats
from bokeh.plotting import figure, output_file, show
output_file("normal_distribution.html")
x = np.linspace(-3, 3, 100)
y = stats.norm.pdf(x, 0, 1)
p = figure(width=400, height=400, title = "Normal Distribution",
tooltips=[("x", "$x"), ("y", "$y")])
p.line(x, y, line_width=2)
show(p)
⑶ 통계량
① 적률생성함수
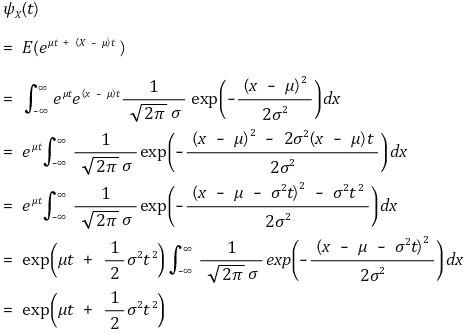
② 평균 : E(X) = μ
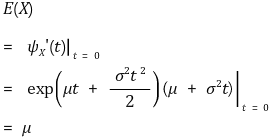
③ 분산 : VAR(X) = σ2
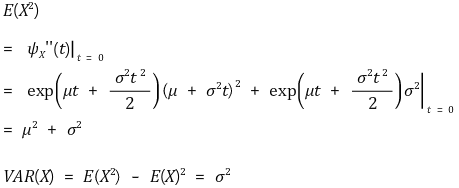
⑷ 성질
① 성질 1. μ를 중심으로 대칭성(symmetric)
② 성질 2. X ~ N(μ, σ2)이면 Y = aX + b ~ N(aμ + b, a2σ2)
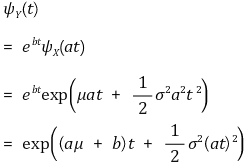
③ 성질 3. Xi ~ N(μi, σi2)이면 X = ∑Xi ~ N(∑μi, ∑σi2)
④ 성질 4. 비상관성 : X와 Y가 jointly normal이고 uncorrelated이면 X와 Y는 독립
⑸ 표준정규분포(standard normal distribution)
① 정의 : 평균이 0, 표준편차가 1인 정규분포
② 정규화(normalization) : X ~ N(μ, σ2)라면, Z = (X - μ) / σ
③ 표준정규분포의 누적분포함수 Φ(z)
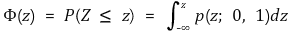
④ zα : X가 zα보다 더 큰 값을 가질 확률이 α가 되는 zα 값
⑹ 정규분포표
Table. 1. 정규분포표
⑺ 예제
① 정규분포 예제
⑻ 응용 1. 로그정규분포(log-normal distribution)
① 정의 : 그 로그가 정규분포를 따르는 확률변수의 분포. 즉, 확률변수 자체는 정규분포를 따르는 확률변수를 지수로 하는 지수함수
② 수식화 : ln X ~ N(μ, σ2)이라면,
○ E[X] = exp(μ + σ2 / 2) (∵ 위 적률생성함수 참고)
○ E[X2] = exp(2μ + 2σ2) (∵ 위 적률생성함수 참고)
○ Var(X) = E[X2] - (E[X])2
○ 표본평균 X̄는 평균이 exp(μ + σ2 / 2)이고 분산이 Var(X) / n인 정규분포를 따른다고 할 수 있음
③ 예시 : 시퀀싱 데이터에서 각 샘플/세포/스팟 별 카운트 값은 로그정규분포를 따름
⑼ 응용 2. 코시분포(Cauchy distribution)
① 정의 : 정규분포를 따르는 두 확률변수 X1과 X2의 비
⑽ 응용 3. 레일리 분포(Rayleigh distribution)
① 정의 : 평균이 0이고 협대역 잡음 신호의 포락선의 순간값
② X와 Y가 N(0, σ2)을 따르는 독립인 확률변수라면 (X2 + Y2)1/2은 Rayleigh(σ2)을 따름
③ 수식화
○ 확률밀도함수
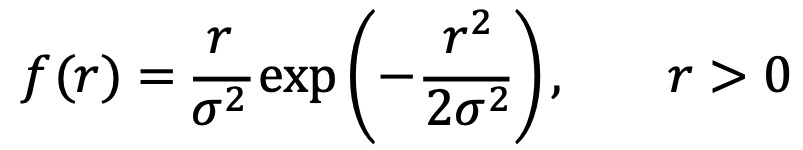
○ 누적분포함수
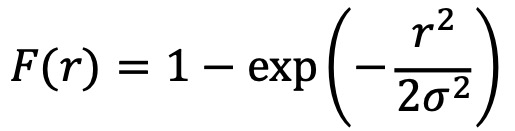
○ 평균과 분산
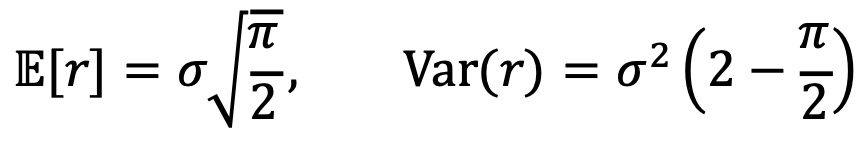
3. 감마분포(gamma distribution) [목차]
⑴ 감마함수(gamma function)
① 정의 1. x ＞ 0에 대해,
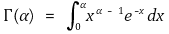
② 정의 2.
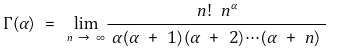
③ 특징
○ Γ(-3/2) = 4/3 √π
○ Γ(-1/2) = -2 √π
○ Γ(1/2) = √π
○ Γ(1) = 1
○ Γ(3/2) = 1/2 √π
○ Γ(a + 1) = aΓ(a)
○ Γ(n + 1) = n!
⑵ 감마분포
① 확률밀도함수 : x, r, λ ＞ 0에 대하여,
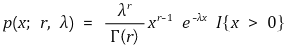
Figure. 3. 감마분포의 확률밀도함수
○ (참고) 파이썬 프로그래밍 (Bokeh)
# see https://www.statology.org/gamma-distribution-in-python/
import numpy as np
import scipy.stats as stats
from bokeh.plotting import figure, output_file, show
output_file("gamma_distribution.html")
x = np.linspace(0, 40, 100)
y1 = stats.gamma.pdf(x, a = 5, scale = 3)
y2 = stats.gamma.pdf(x, a = 2, scale = 5)
y3 = stats.gamma.pdf(x, a = 4, scale = 2)
p = figure(width=400, height=400, title = "Normal Distribution",
tooltips=[("x", "$x"), ("y", "$y")])
p.line(x, y1, line_width=2, color = 'red', legend_label = 'shape=5, scale=3')
p.line(x, y2, line_width=2, color = 'green', legend_label = 'shape=2, scale=5')
p.line(x, y3, line_width=2, color = 'blue', legend_label = 'shape=4, scale=2')
show(p)
② 의미
○ r 번째 사건이 일어날 때까지의 시간의 확률분포
○ r (shape parameter)
○ λ (rate parameter) : 한 단위기간 당 평균 사건 횟수
○ β (scale parameter) : β = 1 / λ
⑶ 통계량
① 적률생성함수
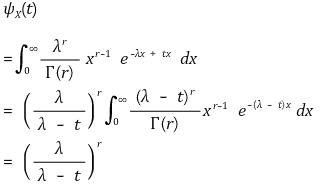
② 평균 : E(X) = r / λ
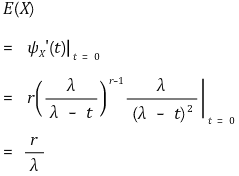
③ 분산 : VAR(X) = r / λ2
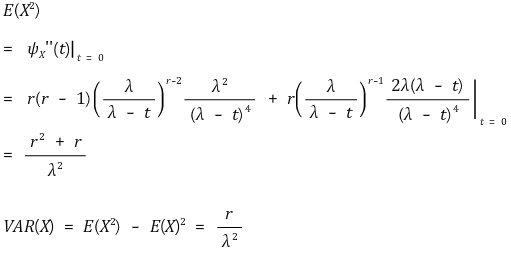
⑷ 다른 확률분포와의 관계
① 이항분포
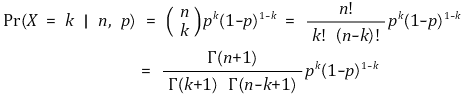
② 음이항분포
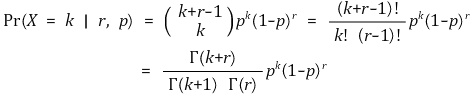
③ 베타분포
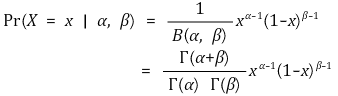
④ 카이제곱분포 : λ = 1/2, r = ν/2인 경우 자유도가 ν인 카이제곱분포가 얻어짐
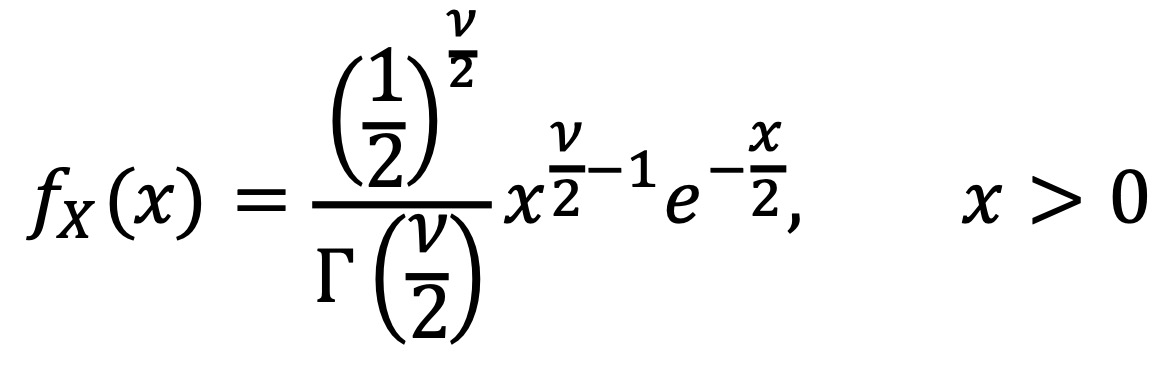
4. 지수분포(exponential distribution) [목차]
⑴ 개요
① 지정된 시점으로부터 어떤 사건이 일어날 때까지 걸리는 시간을 측정하는 확률분포
○ 즉, 첫 번째 사건이 일어날 때까지의 기간
○ 유도 : 단위 시간동안 λ번 일어나는 사건에 대하여,
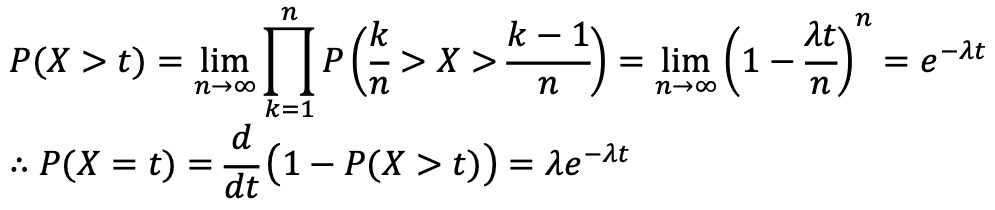
② 감마분포에서 α = 1인 특수한 경우
③ 모수(parameter)의 의미
○ λ (rate parameter) : 한 단위기간 당 평균 사건 횟수
○ β (survival parameter) : λ의 역수. scale이라고도 함
④ (참고) 푸아송분포 : 기간이 고정, 사건의 횟수가 확률변수
⑵ 확률밀도함수 : x ＞ 0에 대하여,
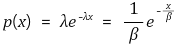
Figure. 4. 지수분포의 확률밀도함수
① (참고) 파이썬 프로그래밍 (Bokeh)
# see https://www.alphacodingskills.com/scipy/scipy-exponential-distribution.php
import numpy as np
from scipy.stats import expon
from bokeh.plotting import figure, output_file, show
output_file("exponential_distribution.html")
x = np.arange(-1, 10, 0.1)
y = expon.pdf(x, 0, 2)
p = figure(width=400, height=400, title = "Exponential Distribution",
tooltips=[("x", "$x"), ("y", "$y")])
p.line(x, y, line_width=2, legend_label = 'loc=0, scale=2')
show(p)
⑶ 통계량
① 적률생성함수
② 평균 : E(X) = 1 / λ
○ 직관적으로 1 / λ임을 알 수 있음
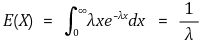
③ 분산 : VAR(X) = 1 / λ2
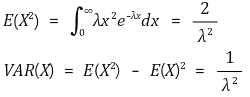
⑷ 무기억성(memorylessness)
① 정의
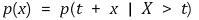
② 예시 : 배터리 수명이 지수분포를 따를 때, 기존 사용 시간이 남은 수명에 영향을 주지 않음
⑸ 지수분포 예제
5. 베타분포(beta distribution) [목차]
⑴ 베타함수(beta function) : α, β ＞ 0에 대하여,
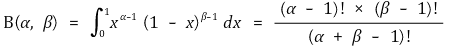
⑵ 베타분포
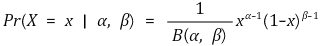
Figure. 5. 베타분포의 확률밀도함수
① (참고) 파이썬 프로그래밍 (Bokeh)
# see https://vitalflux.com/beta-distribution-explained-with-python-examples/
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta
from bokeh.plotting import figure, output_file, show
output_file("beta_distribution.html")
x = np.linspace(0, 1, 100)
y1 = beta.pdf(x, 2, 8)
y2 = beta.pdf(x, 5, 5)
y3 = beta.pdf(x, 8, 2)
p = figure(width=400, height=400, title = "Beta Distribution",
tooltips=[("x", "$x"), ("y", "$y")])
p.line(x, y1, line_width=2, color = 'red', legend_label = 'a=2, b=8')
p.line(x, y2, line_width=2, color = 'green', legend_label = 'a=5, b=5')
p.line(x, y3, line_width=2, color = 'blue', legend_label = 'a=8, b=2')
show(p)
② E(X) = α ÷ (α + β)
③ VAR(X) = αβ ÷ ((α + β)2(α + β + 1))
⑵ 감마함수와의 관계식
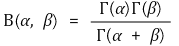
⑶ 성질
① 교환법칙 : B(α, β) = Β(β, α)
② 등가표현
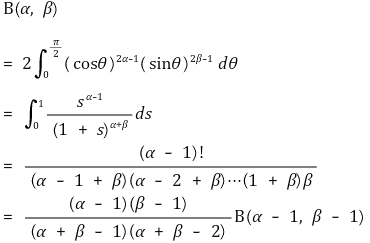
③ 베타이항분포(beta binomial distribution)
○ 베타분포를 갖는 사건을 여러 차례 시행하는 경우에 성공 횟수가 따르는 분포
○ 베타이항분포는 이항분포보다 분산이 큼
⑷ 일반화된 베타분포
6. 파레토 분포(Pareto distribution) [목차]
⑴ 단순 파레토 분포
① 확률밀도함수 : shape parameter a에 대하여,
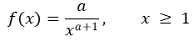
Figure. 6. 기본 파레토 분포의 확률밀도함수
○ (참고) 파이썬 프로그래밍 (Bokeh)
# see https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.pareto.html
import matplotlib.pyplot as plt
from scipy.stats import pareto
from bokeh.plotting import figure, output_file, show
output_file("pareto_distribution.html")
x = np.linspace(1, 10, 100)
y1 = pareto.pdf(x, 1)
y2 = pareto.pdf(x, 2)
y3 = pareto.pdf(x, 3)
p = figure(width=400, height=400, title = "Pareto Distribution",
tooltips=[("x", "$x"), ("y", "$y")])
p.line(x, y1, line_width=2, color = 'red', legend_label = 'a=1')
p.line(x, y2, line_width=2, color = 'green', legend_label = 'a=2')
p.line(x, y3, line_width=2, color = 'blue', legend_label = 'a=3')
show(p)
② 확률분포함수
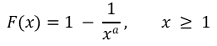
⑵ 일반적인 파레토 분포
① 확률밀도함수 : scale parameter b에 대하여,
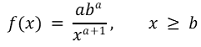
② 확률분포함수
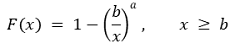
7. 로지스틱 분포(logistic distribution) [목차]
⑴ 단순 로지스틱 분포
① 확률밀도함수
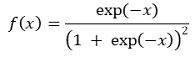
Figure. 7. 단순 로지스틱 분포
○ (참고) 파이썬 프로그래밍 (Bokeh)
# see https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.logistic.html
import matplotlib.pyplot as plt
from scipy.stats import logistic
from bokeh.plotting import figure, output_file, show
output_file("logistic_distribution.html")
x = np.linspace(1, 10, 100)
y = logistic.pdf(x)
p = figure(width=400, height=400, title = "Logistic Distribution",
tooltips=[("x", "$x"), ("y", "$y")])
p.line(x, y, line_width=2)
show(p)
⑵ 일반적인 로지스틱 분포
① 확률밀도함수
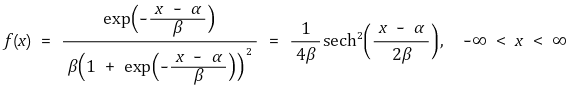
8. 디리클레 분포(Dirichlet distribution) [목차]
⑴ 개요
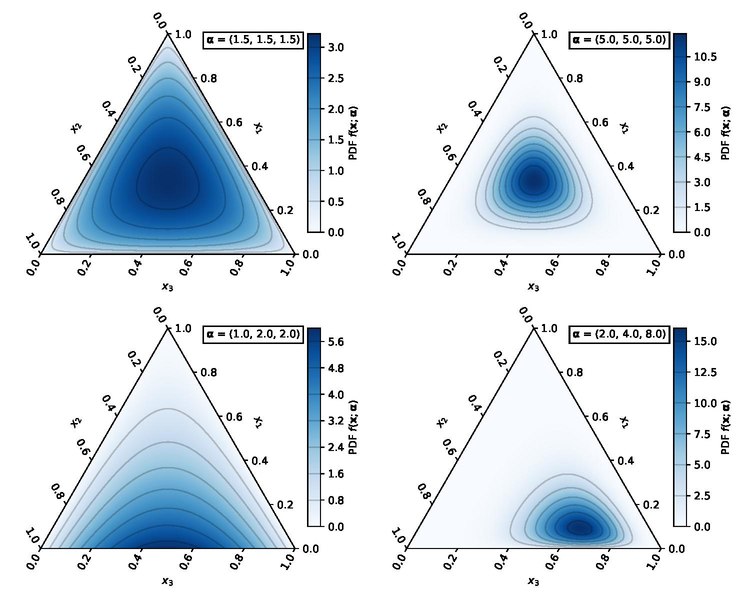
① 베타 분포의 다변량 확장판으로 각 확률변수가 항상 0 ~ 1 사이의 값이고 그 합은 1이어야 함
② 디리클레 분포가 가지는 비율 합이 1로 고정된 제약 조건 때문에, 이 분포를 사용한 최적화는 다른 분포보다 다소 까다로움
③ simplex를 분석할 수 있어서 주목받음
⑵ 확률밀도함수 : x = (x1, ···, xD)와 양수 파라미터 (λ1, ···, λD)에 대하여,
Figure. 8. 디리클레 분포
⑶ Dirichlet-Multinomial conjugacy
9. Gumbel 모델 [목차]
⑴ Gumbel-Softmax
① z를 범주형 변수이고, 각 클래스의 확률이 π1, π2, ···, πk라고 가정
○ 예 : π = [0.2, 0.3, 0.5]
② 범주형 샘플은 k 차원의 one-hot 벡터로 인코딩되며, 이는 (k-1)차원의 simplex인 Δk-1에 존재
○ 이유 : 전체 확률의 합이 1이므로 자유도 1이 감소함
○ 예 : 클래스 1, 2, 3은 각각 [1, 0, 0], [0, 1, 0], [0, 0, 1]에 대응됨
③ Gumbel-Softmax는 softmax를 사용해 연속적인 출력값을 생성하지만, τ가 0에 가까워질수록 Gumbel-Softmax의 출력은 결국 argmax와 동일해져서 one-hot vector가 됨
○ 원래의 xi = log πi는 softmax 함수 통과 후 얻은 y로부터 복원할 수 없음 : 정보가 부족하므로 역변환이 불가능함
○ 이를 보완하기 위해, softmax를 적용하기 전에 마지막 요소 (xk + gk) / τ를 뺀 새로운 샘플링 과정을 정의
⑵ Gumbel 모델
① Gumbel 모델의 확률밀도함수 : scale β = 1, z에서의 평균이 μ일 때,
② 중심화된 multivariate Gumbel의 확률밀도함수
③ 주변확률분포 : 샘플 u1, ···, uk-1에 대하여,
⑶ Gumbel-Softmax 분포의 재파라미터화(reparameterization) (ref)
① 중심화된 Gumbel 분포에서 샘플 u1, ···, uk-1를 얻은 후, 결정론적 변환 h를 적용하면 Gumbel-Softmax의 처음 k-1개 샘플의 좌표를 얻을 수 있음
② Gumbel-Softmax 재파라미터화를 통해 분산이 낮고 미분가능한 범주형 분포를 추정할 수 있음 : 즉, 범주형 변수의 연속변수화
③ 학습 과정에서는 온도가 낮을수록 샘플이 one-hot vector에 가까워지지만 그래디언트의 분산은 커지고, 온도가 높을수록 샘플이 부드러워지지만 그래디언트의 분산이 작아지는 트레이드오프가 존재함 : 실제로는 높은 온도에서 시작해, 낮지만 0이 아는 온도로 서서히 식히는 방식(annealing)을 사용함
④ Gumbel-Softmax는 y ∼qϕ(y | x)를 통해 단일 샘플 그래디언트에 대해 역전파(backpropagation)를 가능하게 하고, 학습 단계당 계산 비용은 𝑂 (D+I+G)로, 크게 향상된 속도를 이룸
○ D : qϕ(y | x)에서 샘플링할 때의 계산 비용
○ I : qϕ(z | x, y)에서 샘플링할 때의 계산 비용
○ G : pϕ(x | y,z)에서 샘플링할 때의 계산 비용
⑤ Gumbel-Softmax와 ST Gumbel-Softmax는 기존의 확률적 gradient 추정 방법들보다 더 우수한 성능을 보임
○ 기존 방법 : Score-Function(SF), DARN, MuProp, Straight-Through(ST), Slope-Annealed ST
입력: 2019.06.19 00:27
수정: 2025.07.15 15:16
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 10강. 통계학 주요 정리 2부 (0) | 2019.06.18 |
|---|---|
| 【통계학】 9강. 통계학 주요 정리 1부 (0) | 2019.06.18 |
| 【통계학】 6강. 이산확률분포 (0) | 2019.06.16 |
| 【통계학】 5강. 통계량 (0) | 2019.06.16 |
| 【통계학】 4강. 확률변수와 분포 (0) | 2019.06.16 |
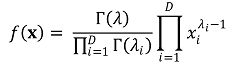
최근댓글