6강.이산확률분포
추천글 : 【통계학】 통계학 목차
1. 균일분포 [본문]
2. 베르누이 분포 [본문]
3. 이항분포 [본문]
4. 다항분포 [본문]
5. 초기하분포 [본문]
6. 기하분포 [본문]
7. 음이항분포 [본문]
8. 음초기하분포 [본문]
9. 푸아송분포 [본문]
Table. 1. 이산확률분포
1. 균일분포(uniform distribution) [목차]
⑴ 정의 : 모든 확률변수에 대해 일정한 확률을 가지는 확률분포
⑵ 확률질량함수 : p(x) = (1 / n) I{x = x1, ···, xn}
Figure. 1. 균일분포의 확률질량함수
① (참고) 파이썬 프로그래밍 (Bokeh)
from bokeh.plotting import figure, output_file, show
output_file("uniform_distribution.html")
graph = figure(width = 400, height = 400, title = "Uniform Distribution",
tooltips=[("x", "$x"), ("y", "$y")] )
x = [1, 2, 3, 4, 5, 6, 7, 8]
top = [1/8, 1/8, 1/8, 1/8, 1/8, 1/8, 1/8, 1/8]
width = 0.5
graph.vbar(x, top = top, width = width, color = "navy", alpha = 0.5)
show(graph)
⑶ 예제
① 균일분포 예제
2. 베르누이 분포(Bernoulli distribution) [목차]
⑴ 베르누이 시행(Bernoulli trials) : 시행 결과가 성공 (X = 1) 또는 실패 (X = 0)인 시행
⑵ 베르누이 분포 : 베르누이 시행을 1회 수행 시의 확률 분포
⑶ 확률질량함수 : p(x) = θ I{x = 1}+ (1 - θ) I{x = 0}
Figure. 2. θ = 0.6일 때, 베르누이 분포의 확률질량함수
① (참고) 파이썬 프로그래밍 (Bokeh)
from bokeh.plotting import figure, output_file, show
output_file("Bernoulli_distribution.html")
x = [0, 1]
top = [0.4, 0.6]
width = 0.5
graph = figure(width = 400, height = 400, title = "Bernoulli Distribution",
tooltips=[("x", "$x"), ("y", "$y")] )
graph.vbar(x, top = top, width = width, color = "navy", alpha = 0.5)
show(graph)
⑷ 통계량
① 적률생성함수

② 평균 : E(X) = θ
③ 분산 : VAR(X) = E(X2) - E(X)2 = θ - θ2 = θ(1 - θ)
3. 이항분포(binomial distribution) [목차]
⑴ 정의 : 베르누이 시행을 n번 반복했을 때 성공의 횟수에 대한 확률분포
① 시행횟수와 시행확률이 고정
⑵ 확률질량함수
① p(x) = nCx θx (1 - θ)n-x
② p(x) : n번 중 딱 x번만 성공했을 때의 확률
③ nCx : 1, 2, ···, n개의 번호표 중 중 x개의 번호표 조합을 뽑을 경우의 수
④ θx : 위 x개의 번호표일 때 성공할 확률
⑤ (1 - θ)n-x : 위 x개의 번호표가 아닐 때 실패할 확률
Figure. 3. n = 30, p = 0.6일 때, 이항분포의 확률질량함수
⑥ (참고) 파이썬 프로그래밍 (Bokeh)
# see https://www.geeksforgeeks.org/python-binomial-distribution/
from scipy.stats import binom
from bokeh.plotting import figure, output_file, show
output_file("binomial_distribution.html")
n = 30
p = 0.6
x = list(range(n+1))
top = [binom.pmf(r,n,p) for r in x]
width = 0.5
graph = figure(width = 400, height = 400, title = "Binomial Distribution",
tooltips=[("x", "$x"), ("y", "$y")] )
graph.vbar(x, top = top, width = width, color = "navy", alpha = 0.5)
show(graph)
⑶ 통계량
① 아이디어 : i 번째 베르누이 시행은 베르누이 분포를 따르므로,

② 적률생성함수

③ 평균 : E(X) = nθ
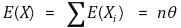
④ 분산 : VAR(X) = nθ(1 - θ)

⑷ 이항분포 예제
4. 다항분포(multinomial distribution) [목차]
⑴ 다항 시행 : 베르누이 시행을 확장하여 발생결과가 셋 이상인 경우
⑵ 다항 분포 : 다항 시행을 n번 반복했을 때의 확률분포
⑶ 확률질량함수

① 전제조건 : x1 + x2 + ··· + xk = n
② p(x1, x2, ··· , xk) = nCx1 × n-x1Cx2 × ··· × xkCxk × θ1x1 θ2x2 ··· θkxk
5. 초기하분포(hypergeometric distribution) [목차]
⑴ 정의 : 전체 N개 중 성공의 개수가 M개라면, n개를 비복원추출로 추출할 때 추출한 성공 개수의 확률분포
⑵ 확률질량함수

혹은 아래 그림과 같은 경우

Figure. 4. [M, n, N] = [20, 7, 12]일 때, 초기하분포의 확률질량함수
① (참고) 파이썬 프로그래밍 (Bokeh)
# see https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.hypergeom.html
from scipy.stats import hypergeom
from bokeh.plotting import figure, output_file, show
output_file("hypergeometric_distribution.html")
[M, n, N] = [20, 7, 12]
rv = hypergeom(M, n, N)
x = np.arange(0, n+1)
top = rv.pmf(x)
width = 0.5
graph = figure(width = 400, height = 400, title = "Hypergeometric Distribution",
tooltips=[("x", "$x"), ("y", "$y")] )
graph.vbar(x, top = top, width = width, color = "navy", alpha = 0.5)
show(graph)
⑶ 통계량
① 평균 : E(X) = nM / N
○ (참고) 이항분포가 E(X) = nθ = nM / N인 것과 유사
② 분산 : VAR(X) = [(N-n) / (N-1)] × [nM / N] × [1 - M / N]
⑷ 이항분포와의 관계
① 이항분포의 조건부 분포 : 초기하분포
② 초기하분포의 극한 (n → ∞) : 이항분포
③ 이항분포는 복원추출이 전제
6. 기하분포(geometric distribution) [목차]
⑴ 정의 : 성공확률이 θ인 추출에 대하여, 성공할 때까지의 시행 횟수에 대한 확률분포
① 시행확률은 고정, 시행횟수는 변함
⑵ 확률질량함수 : p(x) = θ (1 - θ)x-1 I{x = 1, 2, ···}
Figure. 5. θ = 0.5일 때의 기하분포
① (참고) 파이썬 프로그래밍 (Bokeh)
# see https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.geom.html
from scipy.stats import geom
from bokeh.plotting import figure, output_file, show
output_file("geometric_distribution.html")
n = 10
p = 0.6
x = np.arange(0, n+1)
top = geom.pmf(x, p)
width = 0.5
graph = figure(width = 400, height = 400, title = "Geometric Distribution",
tooltips=[("x", "$x"), ("y", "$y")] )
graph.vbar(x, top = top, width = width, color = "navy", alpha = 0.5)
show(graph)
⑶ 통계량
① 적률생성함수

② 평균 : E(X) = 1 / θ
○ 직관적으로 평균 시행 횟수 × 성공확률 = 1이 성립

③ 분산 : VAR(X) = (1 - θ) / θ2

7. 음이항분포(negative binomial distribution) [목차]
⑴ 정의 : 성공 확률이 θ인 경우, r번째 성공이 나올 때까지의 시행횟수에 대한 확률분포
① 이항분포는 시행횟수와 시행확률이 고정, 성공횟수는 변함
② 음이항분포는 성공횟수와 시행확률이 고정, 시행횟수는 변함
⑵ 확률질량함수
① 형태 1. 성공횟수를 r번으로 고정하고 시행횟수를 분석

○ x : 시행횟수
○ r : 성공횟수
○ θ : 성공확률
○ x-1Cr-1 : x번째는 성공이고, 앞의 x-1번의 시행에서 r-1번만 성공한 경우의 수
② 형태 2. 실패횟수를 r*번으로 고정하고 성공횟수를 분석
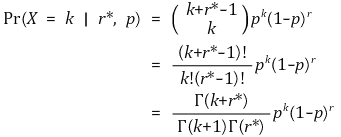
○ k : 성공횟수
○ r* : 실패횟수
○ p : 성공확률
○ k+r*-1Ck : k + r*번째는 실패이고, 앞의 k+r*-1번의 시행에서 r*-1번만 실패한 경우의 수
③ 형태 3. 성공횟수를 r번으로 고정하고 실패횟수를 분석

○ x : 실패횟수
○ r : 성공횟수. size. 1/overdispersion
○ p : 성공확률
④ 그래프
Figure. 6. r = 5, θ = 0.6일 때의 음이항분포의 확률질량함수
⑤ (참고) 파이썬 프로그래밍 (Bokeh)
# see https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.nbinom.html
from scipy.stats import nbinom
from bokeh.plotting import figure, output_file, show
output_file("negative_binomial_distribution.html")
n = 5
p = 0.6
x = np.arange(0, 13)
top = nbinom.pmf(x, n, p)
width = 0.5
graph = figure(width = 400, height = 400, title = "Negative Binomial Distribution",
tooltips=[("x", "$x"), ("y", "$y")] )
graph.vbar(x, top = top, width = width, color = "navy", alpha = 0.5)
show(graph)
⑶ 통계량
① 형태 1에 대한 통계량
○ 아이디어 : X = ∑Xi
○ Xi : i-1번째 성공을 한 후 i번째 성공을 할 때까지의 시행횟수. 기하분포를 따름
○ 적률생성함수

○ 평균 : E(X) = r / θ

○ 분산 : VAR(X) = r(1-θ) / θ2
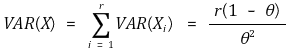
② 형태 2에 대한 통계량
○ 평균 : E(X) = r*p / (1-p)

○ 분산 : VAR(X) = r*p / (1-p)2

③ 형태 3에 대한 통계량
○ 평균 : E(X) = r(1 - p) / p

○ 분산 : VAR(X) = r(1 - p) / p2

○ r, p를 평균과 분산으로 나타낼 수 있음

○ 평균과 분산의 관계 : 분산 = σ2 = 평균 + overdispersion × 평균2 = μ + μ2 / r
⑷ 예제
① 상황 : 매 경기마다 n 종류의 피규어 중 무작위로 하나를 제공
② X : 모든 피규어를 수집할 때까지 관람해야 하는 경기 수
③ 문제 : E(X)
④ 아이디어 : X = X1 + ··· + Xn
⑤ Xi : i번째 새로운 피규어를 수집할 때까지 관람해야 하는 경기 수. 기하분포를 따름
⑥ E(X)

⑸ 응용 1. ZINB(zero-inflated negative binomial distribution)
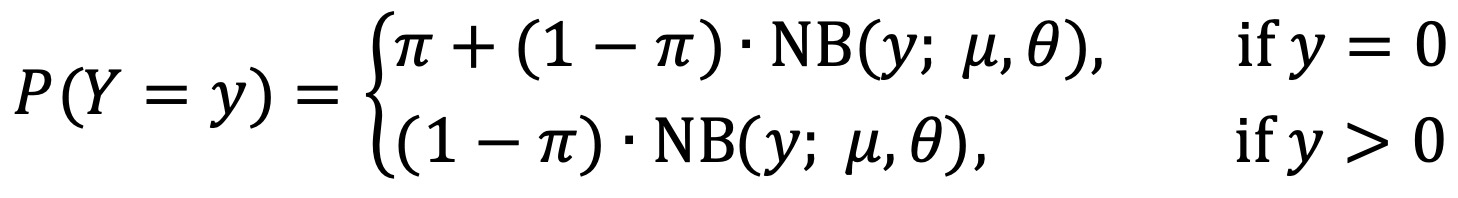
① π : 0이 관찰될 확률
② NB(y; μ, θ) : 평균 μ, dispersion parameter θ를 갖는 음이항분포의 확률질량함수
⑹ 음이항분포 예제
8. 음초기하분포(negative hypergeometric distribution) [목차]
⑴ 정의
① 상황 : 전체 N개 중 성공의 개수가 k개
② 문제 : 비복원추출에서 성공을 r개 뽑았을 때, 그때까지 뽑은 표본의 개수 n
③ 음이항분포와의 유사성 : 뽑은 표본의 개수를 확률변수로 함
④ 초기하분포와의 유사성 : 동일하게 비복원추출 상황을 전제로 함
⑵ 확률질량함수
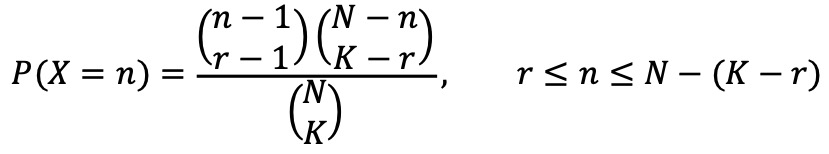
⑶ 통계량
① (참고) 유용한 조합론 공식

② 평균

③ 분산

9. 푸아송분포(포아송분포, Poisson distribution) [목차]
⑴ 개요
① 최초 소개 : "Research on the probability of judgements in criminal & civil matters," 1837, French.
② 정의 : 단위시간 동안 평균 λ번 일어나는 사건에 대해, 단위시간에서 사건이 일어나는 횟수의 확률분포
③ λ : 모수(parameter) (∈ ℝ)
④ 단위 시간의 k배의 시간구간에 대해 λ* = k λ인 푸아송분포로 생각
⑤ 현실적으로 활발하게 이용됨
⑵ 확률질량함수
① 아이디어 : 이항분포와 극한
② 단위시간을 n등분하면 각 등분에서 그 사건이 일어날 확률을 λ / n이라고 할 수 있음
③ 단위시간 동안 사건이 x번 일어날 확률

④ 확률질량함수 : ③에서 n → ∞의 극한을 취하면 됨

⑤ 그래프
Figure. 7. λ = 0.6일 때, 푸아송분포의 확률질량함수
⑥ (참고) 파이썬 프로그래밍 (Bokeh)
# see https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.poisson.html
from scipy.stats import poisson
from bokeh.plotting import figure, output_file, show
output_file("poisson_distribution.html")
lam = 0.6
x = np.arange(0, 4)
top = poisson.pmf(x, lam)
width = 0.5
graph = figure(width = 400, height = 400, title = "Poisson Distribution",
tooltips=[("x", "$x"), ("y", "$y")] )
graph.vbar(x, top = top, width = width, color = "navy", alpha = 0.5)
show(graph)
⑶ 통계량
① 적률생성함수

② 평균 : E(X) = λ

③ 분산 : VAR(X) = λ

④ 평균과 분산이 동일한 이유 : 평균 = np, 분산 = np(1 - p)로 생각할 수 있어서, n → ∞, p → 0으로 극한을 취하면 평균 = 분산이 됨
⑷ 성질
① 푸아송 분포를 따르는 독립인 확률변수의 합은 푸아송 분포를 따름
○ 아래 식에서 확률변수의 합의 적률은 각 적률의 곱과 같음을 이용 (ref)

⑸ 이항분포와의 관계
① 푸아송분포의 조건부 분포 : 이항분포
② 이항분포의 극한 (n → ∞) : 푸아송분포
⑹ 예제
① 상황 : 1시간에 평균 30번 정도의 전화가 걸려 옴
② 문제 : 3분 동안 전화가 2번 걸려올 확률
③ λ = 30이므로, λ* = 30 ÷ 20 = 1.5
④ 계산

⑺ 푸아송분포 예제
입력: 2019.06.18 23:48
수정: 2024.12.22 23:41
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 9강. 통계학 주요 정리 1부 (0) | 2019.06.18 |
|---|---|
| 【통계학】 7강. 연속확률분포 (1) | 2019.06.16 |
| 【통계학】 5강. 통계량 (0) | 2019.06.16 |
| 【통계학】 4강. 확률변수와 분포 (0) | 2019.06.16 |
| 【통계학】 3강. 확률공간 (0) | 2019.06.16 |





최근댓글