4강. 확률변수와 분포(random variable and distribution)
추천글 : 【통계학】 통계학 목차
1. 확률변수(random variable; RV) [목차]
⑴ 정의 : 표본공간 내 각 사건과 대응시키는 함수 또는 대응된 실수값
① 확률변수는 보통 대문자 X로 나타내고, 각 값을 x 또는 xi로 나타냄
② 예 1. Die: {1, ···, 6} → ℝ with Die(i) = i
③ 예 2. Coin: {head, tail} → ℝ with Coin(head) = 1, Coin(tail) = 0
④ 예 3. Sum: {(i, j) | i, j = 1, ···, 6} with Sum(i, j) = i + j
⑤ (참고) X : Ω → ℝ
⑥ (참고) F → B(ℝ) = A, B(ℝ) : Borel field
⑦ (참고) A ⊂ ℝ, X-1(A) = {ω | X(ω) ∈ A}
⑧ (참고) A ⊂ ℝ, PX(A) = P(X-1(A)) : PX는 편의상 P로 표시
⑵ 이산확률변수(discrete random variable)
① 정의 1. 확률변수 X의 치역이 유한집합(finite set) 또는 셀 수 있는 무한집합(countable infinite set)인 경우
② 정의 2. 누적분포함수 F가 이산적인 경우
③ support : 이산확률변수 X에 대하여, P(X = x) ≠ 0인 x의 집합
⑶ 연속확률변수(continuous random variable)
① 정의 1. 확률변수 X의 치역이 셀 수 없는 무한집합(uncountable infinite set)과 관련
② 정의 2. 누적분포함수 F가 연속적인 경우
⑷ 확률분포(probability distribution) : 특정 사건의 확률을 나타내는 함수관계 PX
① 종류 1. 분포함수(distribution function) : 누적분포함수(CDF, cumulative distribution function)라고도 함
② 종류 2. 밀도(density) : 확률질량함수와 확률밀도함수로 구분
③ 종류 3. 적률 생성 함수(moment generating function)
④ 확률질량함수 : 이산확률변수의 확률분포
⑤ 확률밀도함수 : 연속확률변수의 확률분포
⑥ 분포함수를 미분하면 밀도가 됨 ↔ 밀도를 적분하면 분포함수가 됨
2. 분포함수 [목차]
⑴ 정의
① 정의 : F(xi) = P(-∞ < X ≤ xi)인 함수 F를 지칭
② 이산확률변수의 누적분포함수
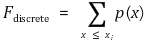
③ 연속확률변수의 누적분포함수
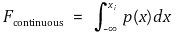
⑵ 성질
① F(-∞) = 0, F(∞) = 1
② x1 < x2에 대하여, F(x1) ≤ F(x2)
③ 밀도가 이산확률변수, 연속확률변수인지 상관없이 우극한은 함수값과 일치
④ P(a < X ≤ b) = F(b) - F(a)
⑶ 각종 확률분포
3. 밀도함수 [목차]
⑴ (참고) 인디케이션 함수(indication function)
① 표기 : I{·}
② 정의 : · 를 만족할 때만 1이고 나머지는 0인 함수
⑵ 확률질량함수(PMF, probability mass function)
① 정의 : X = {x1, x2, ···, xn}에 대해, p(xi) = P(X = xi)인 함수 p(x)를 지칭
② 예시
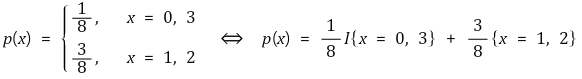
⑶ 확률밀도함수(PDF, probability density function)
① 정의 : 누적분포함수 F에 대해, F'(x) = p(x)인 함수 p(x)를 지칭
② 예시
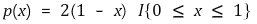
⑷ 공통점
① p(x) ≥ 0
② ∫ p(x) dx = 1
⑸ 차이점
① 점 확률(point probability) : 확률질량함수는 점 확률이 0이 아닐 수 있지만, 확률밀도함수는 점 확률이 항상 0임
② 점 확률이 0인 것과 서포트 함수의 정의는 차이가 있음을 유의
③ 서포트 함수(support function) SX ={x | p(x) > 0}
○ 독립인 경우 서포트 함수가 임의의 변수에 대해서도 일정해야 함
4. 적률 생성 함수 [목차]
⑴ (참고) 기댓값
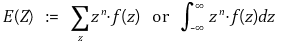
⑵ 적률(moment)
① 원점에 대한 n차 적률
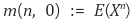
② 원점에 대한 1차 적률(1st moment) : 기댓값
③ 원점에 대한 2차 적률(2nd moment) : 관성모멘트
④ 평균에 대한 1차 적률(central 1st moment) : 0
⑤ 평균에 대한 2차 적률(central 2nd moment) : 분산
⑥ 편포도(왜도, skewness) : 기울어 있는 정도
○ skew > 0 : 우측으로 긴 꼬리가 있는 경우로, 이에 대응하여 많은 데이터가 왼쪽으로 쏠리게 됨
○ skew < 0 : 좌측으로 긴 꼬리가 있는 경우
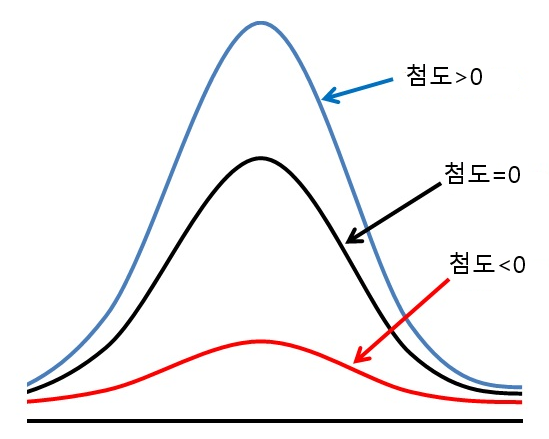
⑦ 첨도(kurtosis) : 뾰족한 정도
Figure. 2. 첨도의 의미
○ 첨도가 3에 가까우면 정규분포와 유사
○ 첨도 ↑ : outlayer가 crazy value가 되려는 경향 ↑, 즉 tailedness가 커짐
○ 첨도 ↑ : 더 뾰족해짐
⑧ 적률 관련 예제
⑶ 적률생성함수(moment generating function)
① 정의
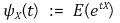
② 적률과의 관계
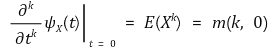
③ 라플라스 변환과 유사 : 적률생성함수와 확률분포는 일대일대응
④ 성질 1. ψaX+b(t) = ebt ψX(at)
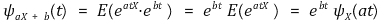
⑤ 성질 2. X1, ···, Xn이 독립이면, Y = X1 + ··· + Xn에 대해
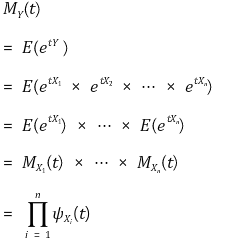
5. 확률생성함수 [목차]
⑴ 확률생성함수(probability generating function) : 주로 이산확률변수에서 정의됨
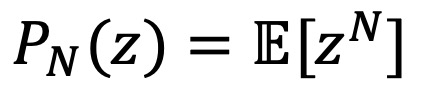
⑵ 적률생성함수와의 관계
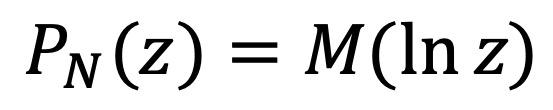
⑶ 서로 독립인 확률변수의 합과 확률생성함수
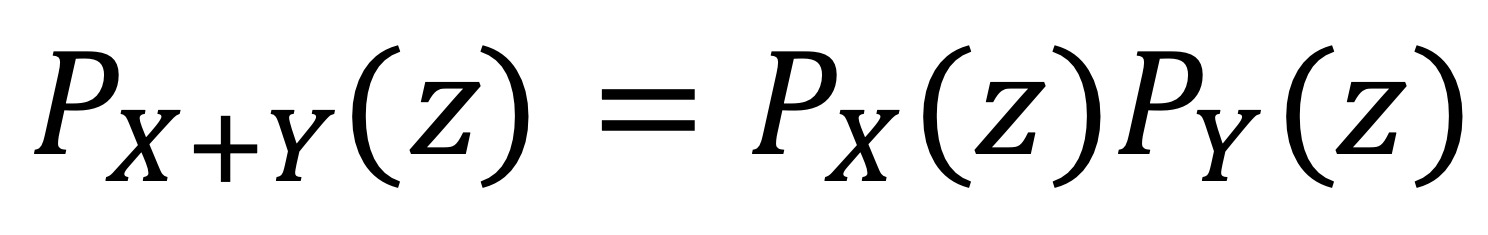
⑷ n차 팩토리얼 모멘트(n-th factorial moment) : μ(n)으로 표시하고 확률생성함수의 n차 도함수로 표현할 수 있음
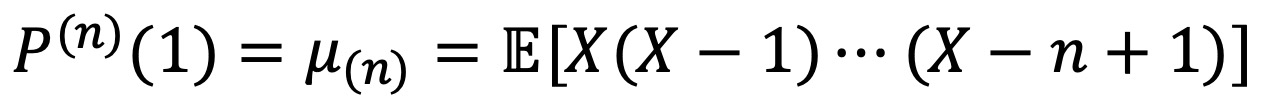
⑸ 확률생성 : pn = Pr(N = n)은 다음과 같음. 테일러 급수에서 xn의 계수로 이해할 수 있음
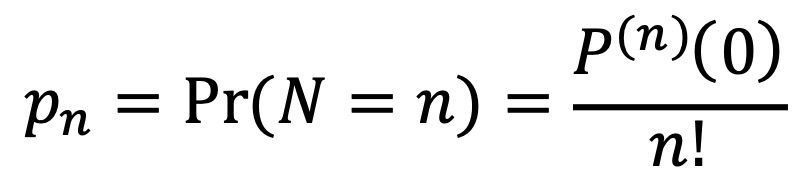
6. 차원의 확장 [목차]
⑴ 확률변수가 두 개가 되도록 (X, Y)를 정의 : Ω → ℝ2
⑵ 결합확률분포(결합확률질량함수, joint probability distribution; 커플링, coupling)
① 이산확률변수 : X = {x1, ···, xm}, Y = {y1, ···, yn}에 대해, p(xi, yj) = P(X = xi, Y = yj)인 함수 p(x, y)
② 연속확률변수 : ∂2F(x, y) / ∂x ∂y = p(x, y)인 함수 p(x, y)
③ 성질 1. p(x, y) ≥ 0
④ 성질 2. ∑∑ p(x, y) = 1
⑶ 주변확률분포(marginal probability distribution)
① 정의 : 결합확률분포를 확률변수 X 또는 Y만의 분포로 바꾼 것
② 이산확률변수의 주변확률분포
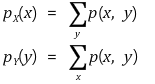
③ 연속확률변수의 주변확률분포

⑷ 예시
Table. 1. 결합확률분포와 주변확률분포의 예
① 결합확률분포를 알면 주변확률분포를 알 수 있음
② 주변확률분포를 안다고 결합확률분포를 항상 알 수 있는 것은 아님
③ 심슨의 역설(Simpson's paradox)
○ 정의 : 데이터의 세부 그룹별로 일정한 경향성이 나타나지만, 전체적으로 보면 그 추세가 사라지거나 반대 경향성을 나타내는 현상
○ 직관적으로 계산하지 않고 수식대로 계산하면 심슨의 역설로 혼란에 빠지지 않을 수 있음
Table. 2. 심슨의 역설
⑸ 결합적률(joint moment)
① 결합적률 예제
⑹ 결합적률생성함수(joint moment generating function)
① 정의
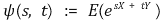
② 성질
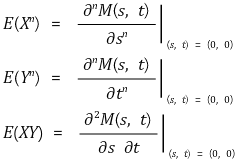
⑺ 조건부 분포(조건부 밀도함수, conditional distribution)
① Y의 조건부 분포 : p (y | x) = p(x, y)/pX(x)
② X의 조건부 분포 : p (x | y) = p(x, y)/pY(y)
③ 응용 1.
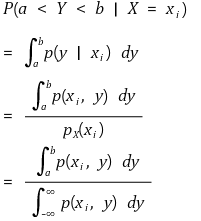
④ 응용 2. Y = g(X), P(X = x) = p(x)에 대해,

⑤ 독립의 조건부 표현
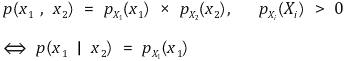
⑥ 조건부 독립(conditional independence)
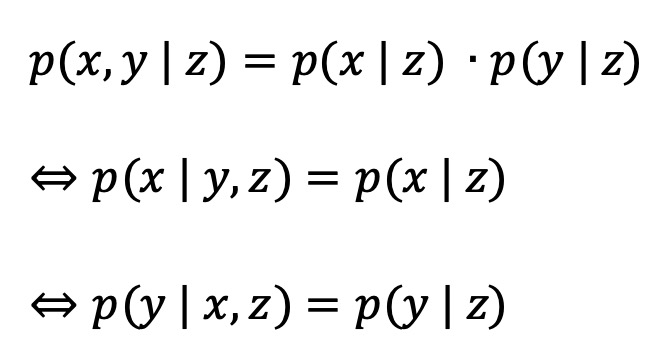
⑻ 상호독립(mutual independence)
① 정의
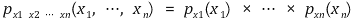
② 상호독립 정의의 완결성
○ 부분에 대해서도 독립이 성립
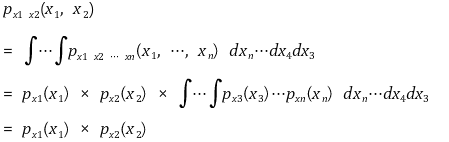
○ 결합 확률 분포와 주변 확률 분포는 상대적인 개념임을 주의
③ 성질 1. 상호독립과 결합분포함수
입력: 2019.06.17 13:52
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 6강. 이산확률분포 (0) | 2019.06.16 |
|---|---|
| 【통계학】 5강. 통계량 (0) | 2019.06.16 |
| 【통계학】 3강. 확률공간 (0) | 2019.06.16 |
| 【통계학】 12강. 오차해석 (오차이론) (0) | 2019.04.13 |
| 【통계학】 2강. 경우의 수 (0) | 2018.09.13 |
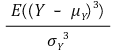

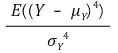






최근댓글