12강. 오차해석(오차이론)
추천글 : 【통계학】 통계학 목차
1. 오차의 본질 [목차]
⑴ 측정 : 엄밀히 정해진 단위에 대해 측정값을 결정하는 것
⑵ 오차 = 측정값 - 참값
⑶ 양자역학의 불확정성 원리에 의해 어떤 측정이든 참값을 정확히 알 수 없음
⑷ 참값이 정확하지 않으므로 오차는 특정 값이라기보다는 특정 범위로 간주되는 게 타당 (확률오차와 관련)
2. 오차의 종류 [목차]
⑴ 부당오차
① 정의 : 계기조작상 분명히 실수를 범하여 측정값이 신빙성이 없는 경우에 생기는 오차
② 예 1. 길이를 재는데 한쪽 원점을 맞추지 않은 경우
③ 예 2. 저항측정에서 원점을 확인하지 않는 경우
④ 해결방법 : 원인이 명백하므로 얻은 데이터를 무시
○ 이들을 포함시킨다면 다른 측정값들의 신빙성이 떨어지기 때문
⑵ 계통오차(systematic error)
① 정의 : 측정계기의 불안정한 상태로 인한 오차
② 특징 : 크기와 부호를 추정할 수 있고 보정할 수 있는 오차
③ 예 1. 전압을 여러 번 측정하여 평균값을 얻었는데 확인결과 사용한 전압계의 눈금이 원점에서 벗어난 경우
④ 예 2. 어떤 자로 길이를 재었는데 온도에 따른 길이의 변화를 고려하지 않는 경우
⑤ 예 3. truncation error : 급수로 표현되는 해에서 특정 항까지만 취함으로써 생기는 오차
⑶ 우연오차(random error)
① 정의 : 반복 측정할 때마다 상이한 결과를 얻게 되는 측정값들의 변동에 기인하는 오차
② 해결방법 : 더 정밀한 측정계기를 사용하거나 여러 번 반복 측정하는 경우
③ 우연오차를 줄이는 문제가 실험결과를 향상시키는 제일 중요한 요소
⑷ 확률오차(probable error)
① 정의 : 측정값을 얻을 때 추정되는 오차의 크기
② 오차의 원인이라기보다는 오차를 표현하는 방법
③ σp로 표시하며 측정값 x = xavg ± σp와 같이 사용
○ x의 오차가 σp라는 의미가 아님
○ x가 ±σp 이상 벗어날 확률이 작다는 의미
○ 참값이 xavg - σp와 xavg + σp 사이에 있을 확률이 50%가 되도록 σp를 설정
④ 오차는 정상분포를 이루며, 오차의 표준편차를 σm이라 하면 참값이 xavg - σm과 xavg + σm 사이에 있을 확률은 약 68 %
⑤ σp = 0.67 σm로 설정하면 참값이 xavg - σp와 xavg + σp 사이에 있을 확률이 50%가 됨
3. 측정값의 유효숫자 [목차]
⑴ 필요성 : 모든 측정값은 근사값이므로 측정값은 효력이 있는 숫자, 즉 유효숫자만을 표시해야 함
⑵ 유효숫자 선택 규칙
① 0이 아닌 맨 왼쪽의 숫자가 최상 유효숫자임
② 소수점이 없을 경우에는 0이 아닌 맨 오른쪽의 숫자가 최하 유효숫자
③ 소수점이 있을 경우에는 맨 오른쪽의 숫자가 0이라도 이 수가 최하 유효숫자
④ 최상 유효숫자와 최하 유효숫자 간의 모든 숫자가 유효숫자
⑤ 예 : 밑줄친 부분만이 유효숫자
○ 994.29
○ 56000
○ 0.0048
○ 6.000
○ 800.
○ 2.990 × 104
⑶ 유효숫자 계산 규칙 : 측정값들을 계산할 때 불필요한 계산시간의 낭비를 줄임
① 덧셈과 뺄셈 : 7.9와 0.1637의 합을 계산하면
○ 숫자 7.9는 소숫점 이하 두 자리에서는 유효숫자가 없으므로 0.1637을 그곳에서 자름 → 0.16
○ 7.9 + 0.16 = 8.06
○ 반올림 하여 소숫점 이하 한 자리가 되도록 하면 8.06 → 8.1
② 곱셈과 나눗셈 : 7.9와 0.1637의 곱을 계산하면
○ 7.9 × 0.1637 = 1.29323
○ 7.9는 유효숫자가 두 자리이고 0.1637은 유효숫자가 네 자리이므로 결과가 두 자리가 되도록 반올림하면 됨
○ 1.29323 → 1.3
4. 표준오차 [목차]
⑴ 필요성 : 측정값들은 우연오차로 인해 어떤 분포를 이룸 → 이들을 대표할 수 있는 수치가 필요
⑵ 종류 1. 최빈값 : 가장 많이 나타나는 측정값
⑶ 종류 2. 중앙값 : 크기 순으로 자료들을 나열했을 때 중앙에 위치한 측정값
⑷ 종류 3. 평균값 : 측정값들의 산술평균
① N개의 측정값들을 x1, x2, ···, xN이라 했을 때
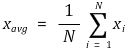
② 만일 각 측정값 x1, x2, ···, xN의 빈도를 각각 f1, f2, ···, fN이라 했을 때
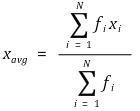
③ 분산(variance) σ2의 계산
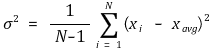
④ 각 회당 한 물리량을 M번씩 측정하면, 매회 얻어지는 측정값에 대한 평균값과 표준편차는 달라짐
⑤ 표본평균 xavg의 표준편차를 σm이라 하면 σ, σm, N 사이에는 다음과 같은 관계가 성립
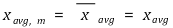
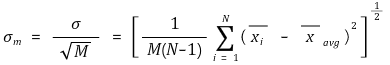
○ σm을 표준오차라고도 부름
⑥ 측정자료들로부터 보고할 측정값은 다음과 같음
x = xavg ± σm
⑦ 일반 물리학실험에서는 신뢰계수를 50 %로 잡는 확률오차를 이용하여 측정값을 보고하는 것이 보통임
x = xavg ± σp = xavg ± 0.6745σm
⑧ 오차를 표기하는 방법
○ 절대오차 : σ의 형태로 보고
○ 상대오차 : σ/|xavg|의 형태로 보고
○ 퍼센트오차 : σ/|xavg| × 100의 형태로 보고
5. 오차의 전파 [목차]
⑴ 예시 : 직육면체의 부피를 구하는 실험
① 경우 1. 1,000개의 부피에 대한 데이터를 얻어 평균값과 표준편차를 구하는 것
② 경우 2. 가로, 세로, 높이에 대한 각각의 평균값을 먼저 구하고 이 평균값들을 곱하여 부피를 구하는 것
③ 경우 2가 훨씬 편리하지만 오차가 누적됨
⑵ 오차의 전파 이론(error propagation theory)
① 어떤 물리량 z가 다른 물리량 x, y, ···의 z = f(x, y, ···)의 관계로 주어졌다고 가정
② x, y, ···의 측정으로부터 xavg, yavg, ···의 평균값(표본평균)과 σx, σy, σz의 표준편차들을 얻었다고 가정
③ z의 평균값 zavg
zavg = f(xavg, yavg, ···)
④ z의 표준편차 σz
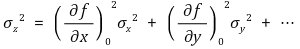
⑤ (∂f/∂x)0, (∂f/∂y)0, ···는 평균값 xavg, yavg, ···에서 계산한 편도함수들을 의미
⑶ 오차의 전파공식
① z = ax ± by
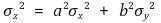
② z = axy
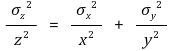
③ z = ax/y
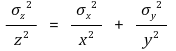
④ z = axb
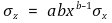
⑤ z = aebx
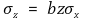
⑥ z = a log(bx)
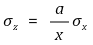
⑷ 제언
① 유효숫자 계산 규칙은 오차의 전파공식으로부터 비롯된 것임
② 멱함수의 경우 지수가 클수록 전파되는 오차량도 커지므로 특히 정밀한 측정이 요구됨
6. 최소 제곱법 [목차]
⑴ 최확값(most probable value) : 편차의 제곱의 합을 극소로 해주는 대표값
⑵ 최소 제곱법
① 한 양을 N번 되풀이하여 측정해서 측정값 x1, x2, ···, xN을 얻었다고 가정
② 최확값을 x라 하면, 편차의 제곱의 합은 다음과 같음
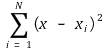
③ 이를 x의 함수로 보고, 이 함수가 극소값을 갖는 조건은 다음과 같음
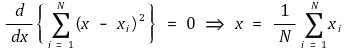
④ 이 경우 최확값은 평균값과 일치함을 알 수 있음
⑶ 다항식 추세선을 구할 때 자주 사용
입력 : 2019.04.13 01:28
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 5강. 통계량 (0) | 2019.06.16 |
|---|---|
| 【통계학】 4강. 확률변수와 분포 (0) | 2019.06.16 |
| 【통계학】 3강. 확률공간 (0) | 2019.06.16 |
| 【통계학】 2강. 경우의 수 (0) | 2018.09.13 |
| 【통계학】 1강. 통계의 기초 (0) | 2018.07.29 |




최근댓글