3강. 확률공간(probability space)
추천글 : 【통계학】 통계학 목차
a. 포함배제의 원리
b. 몬티홀 문제
1. 집합론(set theory) [목차]
⑴ 결과(경우, outcome) : 임의로 정의 가능. ωi로 표시
⑵ 표본공간(sample space) : 다음 조건을 만족하는 집합 Ω
① Ω = { ω1, ω2, ···, ωn}
② ωi와 ωj는 배반(disjoint) : 각 ω를 atomic event라고 함
③ Ω는 가능한 모든 결과를 포함
④ {{1, 2, 3}, {3, 4, 5, 6}} (×)
⑤ {{1, 2}, {3, 4, 5, 6}} (○)
⑶ 필드(field) : Ω의 모든 부분집합의 집합 F
① 가정 : Ω = {1, 2, 3}
② F = {∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}
⑷ 사건(events) : F의 각 원소, 즉 표본공간의 부분집합
① 전사건(total event) : Ω
② 공사건(null event) : ∅
③ 여사건(complementary event) : Ac = Ω - A
④ 합사건(union event) : A ∪ B
⑤ 곱사건(intersection event) : A ∩ B
⑥ 배반사건(mutually exclusive events) : A ∩ B = ∅인 사건 A, B의 관계
⑦ 사건의 개수 : 경우의 수가 n일 때 2n개
⑧ 드 모르간 법칙(De Morgan's law) : (E ∪ F)c = Ec ∩ Fc, (E ∩ F)c = Ec ∪ Fc
⑸ 확률(probability)
① 직관적 정의 : 특정 사건의 확률 = 특정 사건의 경우의 수 ÷ 모든 경우의 수
② axiomatic approach : 통계학의 아버지 Kolmogorov가 제안
○ 확률은 함수의 일종 : F → ℝ
○ 공리 1. P(E) ≥ 0
○ 공리 2. P(Ω) = 1
○ 공리 3. 확률의 덧셈정리(addition rule) : 배반인 Ei와 Ej에 대해
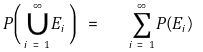
○ 유도 1. P(∅) = 0
○ P(U) = P(U) + P(∅) ⇔ P(∅) = 0
○ E ≠ ∅임에도 P(E) = 0일 수 있음을 유의
○ 유도 2. P(Ec) = 1 - P(E)
○ 1 = P(E ∪ Ec) = P(E) + P(Ec)
○ 유도 3. E ⊂ F → P(E) ≤ P(F)
○ F = E ∪ (Ec ∩ F) → P(F) = P(E) + P(Ec ∩ F) ≥ P(E)
○ 유도 4. P(E ∪ F) = P(E) + P(F) - P(E ∩ F)
○ E ∪ F = (Ec ∩ F) ∪ (E ∩ F) ∪ (E ∩ Fc)
○ P(E ∪ F) = (P(F) - P(E ∩ F)) + P(E ∩ F) + (P(E) - P(E ∩ F))
○ 유도 5. 드 모르간 법칙(De Morgan's law)
○ (A ∪ B)c = ((Ac ∩ B) ∪ (A ∩ Bc) ∪ (A ∩ B))c = (U - Ac ∩ Bc)c = Ac ∩ Bc
○ C = Ac, D = Bc라 두면, C ∩ D = (Cc ∪ Dc)c ⇔ (C ∩ D)c = Cc ∪ Dc
③ 크롬웰의 규칙(Cromwell's rule) : 논리적 문장을 제외하고는 1 또는 0의 확률로 현상을 해석하지 말라는 의미
⑹ 포함배제의 원리(inclusion-exclusion principle)
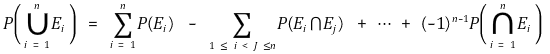
① 예 : P(A ∪ B ∪ C) = P(A) + P(B) + P(C) - P(A ∩ B) - P(B ∩ C) - P(C ∩ A) + P(A ∩ B ∩ C)
⑺ 집합론 예제
2. 조건부 확률(conditional probability) [목차]
⑴ 조건부 확률
① P(A | B) : 사건 B가 일어났을 때 사건 A가 일어날 확률
② 표현 : P(A | B) = P(A ∩ B) ÷ P(B)
③ P(A | B) ≠ P(B | A)
④ 확률의 곱셈정리(multiplication rule) : P(A ∩ B) = P(A) × P(B | A) = P(B) × P(A | B)
⑤ 전제가 둘 이상일 때의 확률의 곱셈정리
○ 어떤 확률을 구하더라도 암묵적으로 특정 전제조건(e.g., α, β)이 존재하므로 다음 식은 자명하게 성립
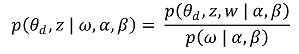
⑵ 조건부 확률의 연쇄법칙(chain rule of conditional probability)
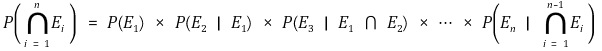
① 예 : P(A ∩ B ∩ C) = P(A) × P(B | A) × P(C | A ∩ B)
⑶ 사건의 독립(independence) : 조건부 확률이 내재 확률과 동일한 경우
① 개요
○ 정의 : P(A ∩ B) = P(A) × P(B)
○ A ⊥⊥ B는 A와 B가 독립임을 나타냄
② 응용
○ P(A | B) = P(A ∩ B) ÷ P(B) = P(A)
○ P(B | A) = P(A ∩ B) ÷ P(A) = P(B)
○ E와 F가 독립 ⇔ Ec와 F가 독립 ⇔ E와 Fc가 독립 ⇔ Ec와 Fc가 독립
○ P(A) = 0이면 A와 B는 항상 독립
○ P(A), P(B) > 0이고 A와 B가 독립 → A와 B는 배반(disjoint)이 아님
○ A와 B가 배반이면 P(A) = 0, P(B) = 0 또는 A와 B가 not independent (대우명제)
○ A, B, G가 서로 독립이어도 A ∩ B와 G가 독립이 아닐 수 있음 : 예를 들어, A는 첫 번째 동전이 앞면인 경우, B는 두 번째 동전이 앞면인 경우, G는 두 번의 토스가 같은 면인 경우
③ 직관적 의미
○ 한 변수에 대한 정보가 다른 변수에 대한 어떤 정보도 알려주지 않음
④ (참고) 조건부 확률과의 관계
○ Pr(X = x | Y = y) = Pr(X = x)
⑷ 상호독립(mutual independence)
① 조건 1.
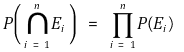
② 조건 2. 조건 1을 포함
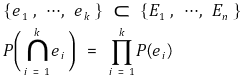
③ (구별개념) pairwise independence
○ 정의 : P(Am ∩ Ak) = P(Am) × P(Ak),∀ m, k
○ mutual independence ⊆ pairwise independence
○ 일반적으로 여러 사건의 independence는 mutual independence를 의미함
⑸ 조건부독립(conditional independence)
① 정의
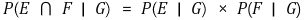
② 조건부 독립이라고 항상 독립인 것은 아님
③ 독립이라고 항상 조건부 독립인 것은 아님
⑹ 전확률의 법칙(law of total probability)
① 분할(partition)
○ 정의 1. (exhaustive) Ω = B1 ∪ B2 ∪ ··· ∪ Bn
○ 정의 2. (disjoint) Bi ∩ Bj = ∅
② 결론
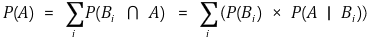
○ 팁 : 벤 다이어그램을 그리면 쉽게 이해 가능
③ 중요성 : 베이즈 정리 유도에 활용
⑺ 베이즈 정리(Bayes' theroem)
① 가정 1. S = B1 ∪ B2 ∪ ··· ∪ Bn
② 가정 2. ∀ i, j, Bi ∩ Bj = ∅
③ 결론
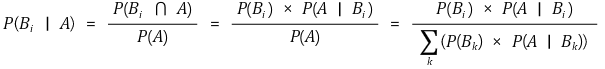
④ 중요성 1. P(B | A)를 계산하기 위해 전혀 무관한 P(A | B)를 이용할 수 있음
⑤ 중요성 2. 결과(posterior, a posteriori)를 보고 원인(prior, a priori)을 예측 가능
○ A : 결과로 관찰되는 사건
○ B : 원인이 되는 사건
○ P(Bi) : prior
○ P(Bi | A) : A가 관찰시 Bi가 원인이었을 확률 (posterior)
○ P(A | Bi) : Bi가 원인이었을 때 A가 일어날 확률 (likelihood)
⑥ (참고) 베이즈 통계학
○ 모집단을 확정하기 않고 확률을 추론
○ 확률은 인간의 믿음에 불과하다고 주장
⑻ 예제 1. 진단율
① 암 환자 비율
P(A) = 1%
② 진단시 양성 확률(적중률)
P(B)
③ 암 환자 진단시 양성 확률
P(B | A) = 95%
④ 암 환자가 아닌 사람을 진단시 거짓양성 확률
P(B | Ac) = 5%
⑤ 문제 : 진단시 양성인 사람이 정말 암에 걸렸을 확률
P(A | B)
⑥ 진단시 양성비율 : 전확률의 법칙 이용
P(B) = P(B | A) + P(B | Ac) = 0.95 × 0.01 + 0.05 × 0.99
⑦ 임의의 사람이 암 환자이면서 진단시 양성 비율인 확률
P(A ∩ B) = P(B | A) × P(A) = 0.95 × 0.01
⑧ 답
P(A | B) = P(A ∩ B) ÷ P(B) = 0.16
⑨ 해석 : 암 환자가 아닌 사람이 많으므로 거짓양성 비율이 상당히 많음
⑼ 예제 2. 몬티홀 문제(Monty hall problem)
① 상황
○ 세 개의 문 중 한 개의 문 뒤에 슈퍼카가 대기
○ 쇼 참가자는 세 개의 문 중 한 개의 문을 선택
○ 쇼 진행자는 쇼 참가자가 열지 않은 문 중 임의로 하나를 개방
○ 쇼 참가자는 기존의 선택을 고수하거나 선택을 바꿀 수 있음
○ 문제 : 어떤 선택이 합리적인가?
② 전제
○ 쇼 참가자는 최초에 1번 문을 선택
○ 쇼 진행자는 3번 문을 개방
③ 정의
○ P(ⅰ) : 1번 문 뒤에 슈퍼카가 있을 확률
○ P(ⅱ) : 2번 문 뒤에 슈퍼카가 있을 확률
○ P(ⅲ) : 3번 문 뒤에 슈퍼카가 있을 확률
○ P(Ⅰ) : 쇼 진행자가 1번 문을 선택할 확률
○ P(Ⅱ) : 쇼 진행자가 2번 문을 선택할 확률
○ P(Ⅲ) : 쇼 진행자가 3번 문을 선택할 확률
○ P(ⅰ), P(ⅱ), P(ⅲ)는 사전확률(원인)
○ P(Ⅰ), P(Ⅱ), P(Ⅲ)는 사후확률(결과)
④ 조건부 확률
○ P(ⅰ | Ⅲ) : 쇼 진행자가 3번 문을 선택했을 때, 1번 문 뒤에 슈퍼카가 있을 확률
○ P(Ⅲ | ⅰ) : 1번 문 뒤에 슈퍼카가 있을 때, 쇼 진행자가 3번 문을 선택할 확률
⑤ 베이즈 정리
○ P(ⅰ | Ⅲ)
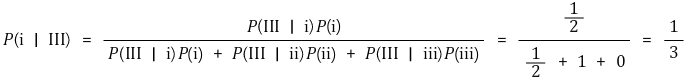
○ P(ⅱ | Ⅲ)
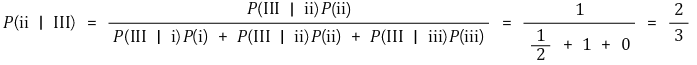
○ P(ⅲ | Ⅲ)
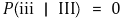
⑥ 결론 : 쇼 참가자는 최초의 선택을 바꾸는 게 유리함
입력 : 2019.06.16 22:02
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 5강. 통계량 (0) | 2019.06.16 |
|---|---|
| 【통계학】 4강. 확률변수와 분포 (0) | 2019.06.16 |
| 【통계학】 12강. 오차해석 (오차이론) (0) | 2019.04.13 |
| 【통계학】 2강. 경우의 수 (0) | 2018.09.13 |
| 【통계학】 1강. 통계의 기초 (0) | 2018.07.29 |




최근댓글