2강. 경우의 수(number of cases)
추천글 : 【통계학】 통계학 목차
a. 경우의 수 예제
1. 개요 [목차]
⑴ 추출(sampling)
① 복원추출(with-replacement) : 이미 추출한 것을 다시 넣고 추출하는 것
② 비복원추출(without-replacement) : 이미 추출한 것을 다시 넣지 않고 추출하는 것
⑵ 경우의 수 종류
Figure. 1. 경우의 수 종류
2. 순열(permutation) [목차]
⑴ 개요
① 정의 : n개의 공 중 k개의 공의 순서의 경우의 수. 순서 고려. 비복원추출
② 즉, 서로 다른 n개에서 중복되지 않게 r개를 택하여 일렬로 나열하는 것
③ nPr = n(n-1)···(n-r+1) (참고로, n! = n(n-1)···2·1)
④ 예시 : 한 줄로 세우기, 대표 뽑기 (서로 다른 역할)
⑵ 종류
① 중복순열(permutation with repetition) : 순서 고려. 복원추출
② 동자순열(permutation of multisets) : 같은 것이 있는 순열
③ 원순열(circular permutation) : 원탁에 둘러앉는 경우의 수
3. 조합(이항계수, combination) [목차]
⑴ 개요
① 정의 : n개의 공 중 k개의 공의 조합의 경우의 수 (순서 미고려, 비복원추출)
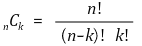
② 즉, 서로 다른 n개에서 순서를 생각하지 않고 중복되지 않게 r개를 택하는 것
③ 예시 : 선택하는 경우, 대표 뽑기 (서로 같은 역할)
⑵ 이항계수는 파스칼의 삼각형으로 표현 가능
Figure. 2. 이항계수와 파스칼의 삼각형
⑶ 중복조합(combination with repetition)
① 정의 : 순서 미고려, 복원추출
nHk
② 등가표현
a1 + ··· + an = k, ai ≥ 0
⇔ A1 + ··· + An = k+n, Ai ≥ 1
⇔ □ | □ | ··· | □, □ : (k+n)개, | : (k+n-1)개
⇔ nHk = n+k-1Cn-1 = n+k-1Ck
⑷ 공식 1. n개 중 r개를 선택하는 경우의 수와 선택하지 않은 n-r개를 고르는 경우의 수가 반드시 동일함
nCr = nCn-r
⑸ 공식 2.
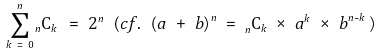
⑹ 공식 3.
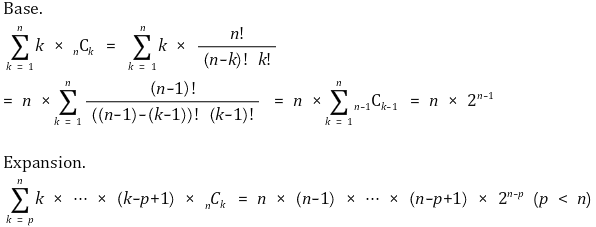
⑺ 공식 4.
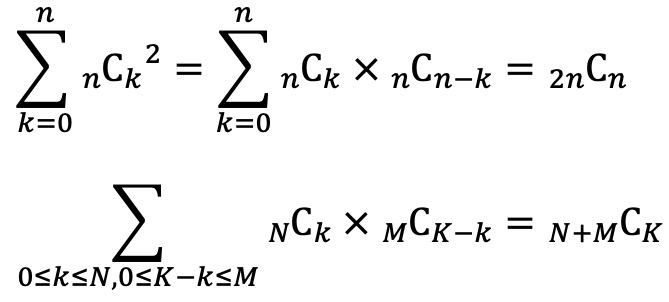
① 조합론적 해석
○ 첫 번째 수식 : 2n개의 자리를 왼쪽 n개, 오른쪽 n개로 나누고, n개의 돌을 각 자리에 분배하는 경우의 수
○ 두 번째 수식 : N+M개의 자리를 왼쪽 N개, 오른쪽 M개로 나누고, K개의 돌을 각 자리에 분배하는 경우의 수
⑻ 공식 5.
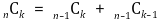
① 대수적 해석

② 조합론적 해석
○ nCk : n개 중 k를 뽑는 경우의 수
○ n-1Ck : 특정 1개를 제외한 k개를 뽑는 경우의 수
○ n-1Ck-1 : 특정 1개를 포함한 k개를 뽑는 경우의 수
⑼ 공식 6.
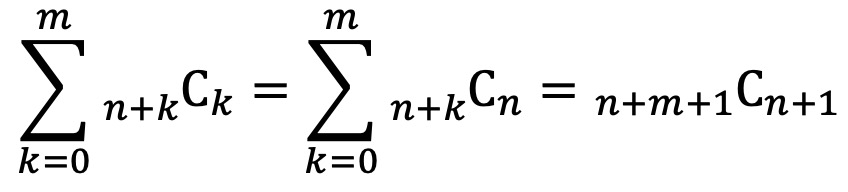
① 대수적 해석
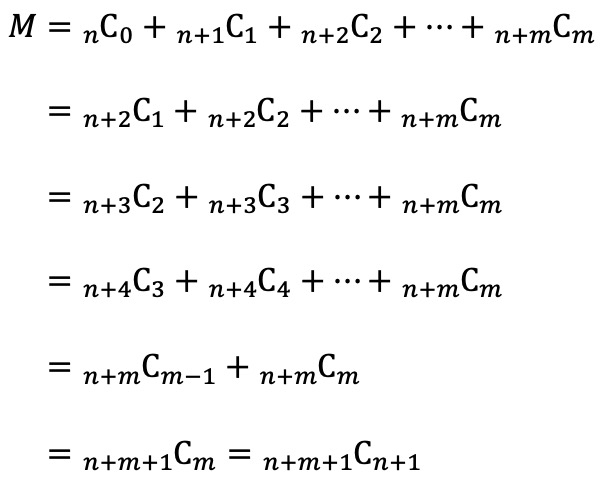
② 조합론적 해석
○ 상황 : 1부터 n+m+1까지의 숫자 중 n+1개를 뽑는 조합의 수
○ nCn : n+1이 가장 큰 숫자가 되는 조합의 수
○ n+1Cn : n+2가 가장 큰 숫자가 되는 조합의 수
○ n+mCn : n+m+1이 가장 큰 숫자가 되는 조합의 수
⑽ 공식 7.

① 대수적 해석
② 조합론적 해석
○ 앞면 또는 뒷면이 n+1번 나올 때까지 동전을 던질 확률 = 1
○ nCn × (½)n+1 × 2 : 맨 마지막과 같은 면이 n번, 맨 마지막과 다른 면이 0번 나온 확률
○ n+1Cn × (½)n+2 × 2 : 맨 마지막과 같은 면이 n번, 맨 마지막과 다른 면이 1번 나올 확률
○ 2nCn × (½)2n+1 × 2 : 맨 마지막과 같은 면이 n번, 맨 마지막과 다른 면이 n번 나올 확률
⑾ 공식 8.
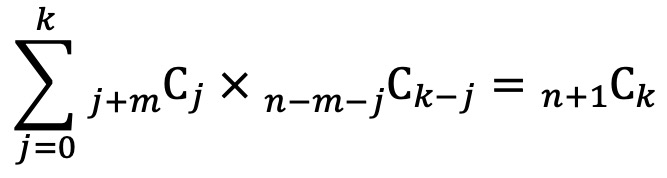
① 대수적 해석
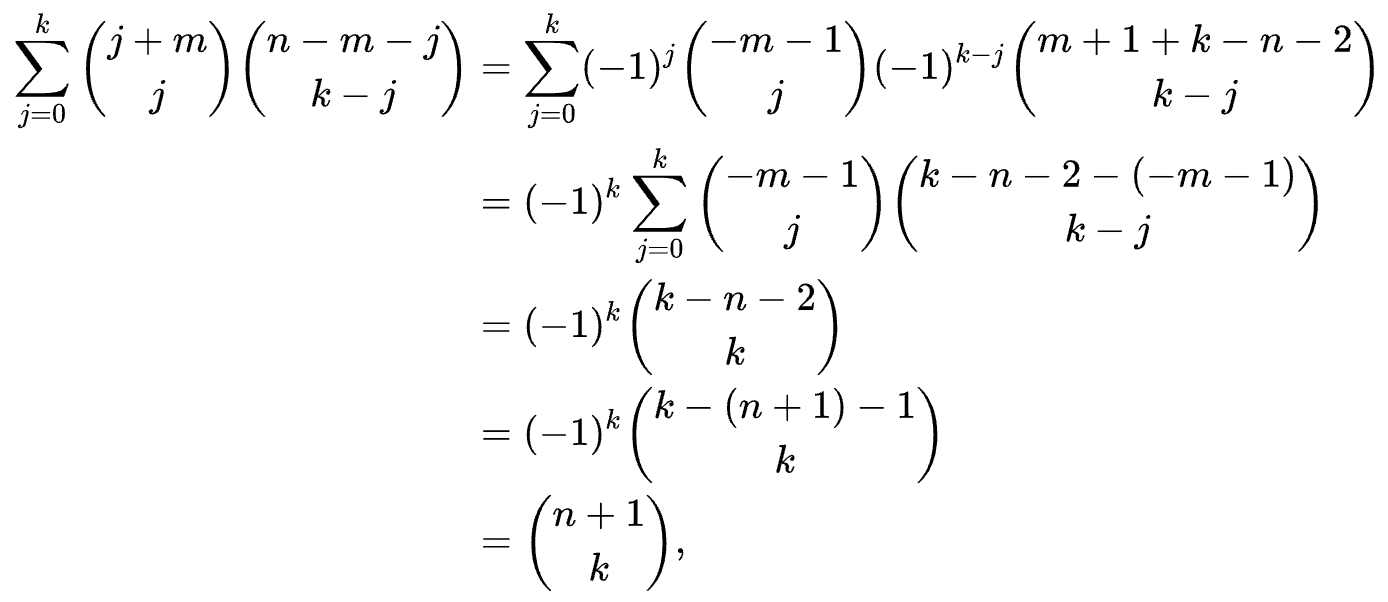
② 조합론적 해석
○ n개의 돌 중 검은 돌이 k개, 흰 돌이 (n-k)개라고 가정. 1개의 특별한 검은 돌을 추가하고, 이 특별한 검은 돌이 반드시 (m+1)번째 검은 돌이 되게 한다고 가정. 이때, 각 j ∈ {0, ⋯, k}에 대하여 그 검은 돌 앞에는 (j+m)개의 돌(이 중 m개의 검은 돌을 분배해야 하므로 j+mCj를 고려)이 있고, 그 검은 돌 뒤에는 (n-m-j)개의 돌(이 중 (k-j)개의 검은 돌을 분배해야 하므로 n-m-jCk-j를 고려)이 있게 됨
○ 전체 경우의 수는 검은 돌 (k+1)개, 흰 돌 (n-k)개를 분배하는 경우의 수에 불과하므로 n+1Ck.
입력: 2019.06.27 09:48
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 5강. 통계량 (0) | 2019.06.16 |
|---|---|
| 【통계학】 4강. 확률변수와 분포 (0) | 2019.06.16 |
| 【통계학】 3강. 확률공간 (0) | 2019.06.16 |
| 【통계학】 12강. 오차해석 (오차이론) (0) | 2019.04.13 |
| 【통계학】 1강. 통계의 기초 (0) | 2018.07.29 |






최근댓글