5강. 통계량(statistical quantity)
추천글 : 【통계학】 통계학 목차
a. SSIM
b. 거리함수와 유사도
1. 기댓값(expectation) [목차]
⑴ 정의 : 확률변수 X의 기댓값 E(X)는 시행 결과 평균적으로 얻어지는 X 값
① 이산확률변수

② 연속확률변수

⑵ 결합확률분포함수
① 이산확률변수

② 연속확률변수

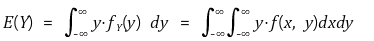
⑶ 기댓값의 성질
① 선형성(linearity) : E(aX + bY + c) = aE(X) + bE(Y) + c
② X와 Y가 독립일 때, E(XY) = E(X) × E(Y)
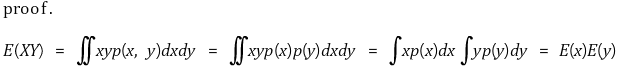
⑷ 예제
① X : n명의 모자를 섞고 각자 1개씩 비복원추출 시, 올바르게 자신의 모자를 찾은 사람의 수
② 문제 의도 : p(X)를 구한 뒤 E(X)를 계산하는 것은 어려움
③ X = X1 + ··· + Xn, Xi : i번 사람이 자신의 모자를 찾은 경우 1, 아닌 경우 0
④ 접근 1. 경우의 수 접근
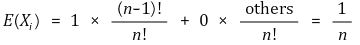
⑤ 접근 2. i번 사람이 최초로 추출한 때나 그렇지 않은 때의 기댓값은 대칭성에 의해 일정
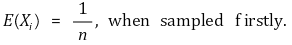
⑸ (참고) 코시 분포(Cauchy distribution) : 기댓값이 정의되지 않음
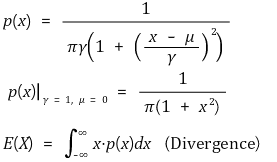
⑹ 기댓값 예제
2. 표준편차 [목차]
⑴ 편차(deviation)
① 정의 : D = X - E(X)
② 성질 1. E(D) = E(X - E(X)) = E(X) - E(X) = 0
⑵ 분산(variance, VAR)
① 정의 : E(X) = μ라 할 때, VAR(X) = E((X - μ)2) = E(D2)
② 성질 1. VAR(X) = E(X2) - μ2
○ 유도 : VAR(X) = E((X - μ)2) = E(X2) - 2μE(X) + μ2 = E(X2) - 2μ2 + μ2 = E(X2) - μ2
③ 성질 2. VAR(aX + b) = a2 VAR(X)
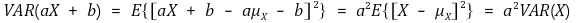
④ 성질 3. 공분산 도입 : VAR(X + Y) = VAR(X) + VAR(Y) + 2 COV(X, Y)
○ R.A. 피셔(R.A. Fisher)에 의해 1936년에 만들어짐
○ 유도
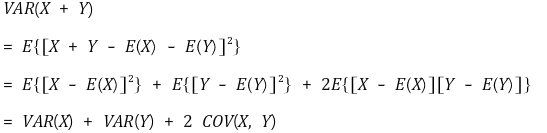
○ 일반화된 유도
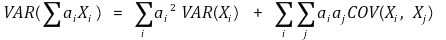
○ 선형성 : X와 Y가 독립이면, VAR(X + Y) = VAR(X) + VAR(Y)
○ 공분산의 정의 : 중복되지 않는 (x1, y1), ···, (xn, yn)의 데이터 세트가 주어져 있을 때 x와 y의 공분산은 다음과 같이 주어짐
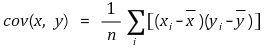
○ 만일 중복을 허용하면 표본비율 pi를 도입하여 공분산의 정의는 다음과 같이 변형됨 : 이때 yi = xi라면 공분산 = 분산이 됨
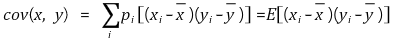
○ 2차원 공분산 행렬 Σ (단, x = (x1, x2)T = (x, y)T)
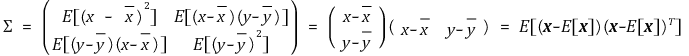
○ Σ = E[ (x-E[x]) (x-E[x])T ]는 2차원뿐만 아니라 n차원에 대해서도 성립
⑤ 성질 4. VAR(X) = 0 ⇔ P(X = constant) = 1 (Chebyshev 부등식)
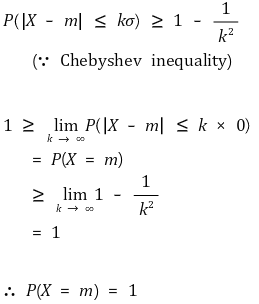
⑥ 분산 예제
⑶ 표준편차(standard deviation, SD)
① 정의 : X의 표준편차 σ 또는 SD(X)는 σ = √ VAR(X) ⇔ σ2 = VAR(X)
② 취지 : X와 분산은 단위가 같지 않지만, X와 표준편차는 단위가 같음
③ 성질 : VAR 및 σ는 양의 값을 가짐, 공분산의 부호를 판단할 때 알아야 함
⑷ 변동계수(coefficient of variation, CV)
① 표준편차를 평균으로 나눈 값
② 측정 단위가 서로 다른 자료의 흩어진 정도를 상대적으로 비교할 때 사용
⑸ 평균 절대 편차(MAD, mean absolute deviation)
① 평균 혹은 중앙값 x̄에 대하여
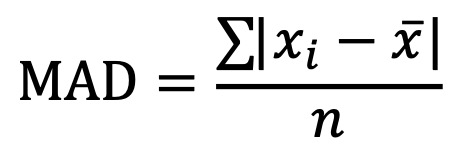
3. 공분산과 상관계수 [목차]
⑴ 공분산(covariance, COV)
① 정의 : E(X) = μx, E(Y) = μy에 대해, 다음과 같이 정의
COV(X, Y) = σxy = E{(X - μx)(Y - μy)}
② 의미 : X가 변할 때 Y가 변하는 정도
③ 성질 1. COV(X, Y) = E(XY) - E(X)E(Y)
○ 유도 : COV(X, Y) = E((X - μx)(Y - μy)) = E(XY) - μxE(Y) - μyE(X) + μxμy = E(XY) - μxμy
④ 성질 2. X = Y이면 COV(X, Y) = VAR(X)
⑤ 성질 3. X와 Y가 독립이면 COV(X, Y) = 0
○ 유도 : COV(X, Y) = E(XY) - E(X)E(Y) = E(X)E(Y) - E(X)E(Y) = 0
○ 독립은 더 엄격한 조건이기 때문에 COV(X, Y) = 0이라고 하여 X와 Y가 독립이라고 단정할 수 없음
⑥ 성질 4. COV(aX + b, cY + d) = ac COV(X, Y)
⑦ 성질 5. COV(a1 X1 + a2 X2, Y) = a1 COV(X1, Y) + a2 COV(X2, Y)
⑧ 한계 : 성질 4에 의해 공분산은 연관성과 크기 정보를 모두 포함하므로 연관성만을 말할 수 없음
⑨ 공분산 예제
⑵ 피어슨 상관계수(Pearson correlation coefficient) : 단순히 상관계수라고도 함
① 정의 : X와 Y의 표준편차 σx, σy에 대해,
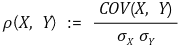
○ 다중상관계수 : 변수가 3개 이상일 때 상관계수를 나타낸 것
○ 완전상관(complete correlation) : ρ = 1
○ 상관 없음(no correlation) : ρ = 0
② 도입배경 : 크기 정보를 제외하고 연관성 정보만 나타내기 위함. 공분산의 한계와 관련
③ 특징
○ 등간, 비율척도로 측정된 두 변수들의 상관관계
○ 연속형 변수를 대상으로 함
○ 정규성 가정
○ 대부분 많이 사용
④ 성질 1. -1 ≤ ρ(X, Y) ≤ 1 (correlation inequality)
○ 증명 : 코시-슈바르츠 부등식
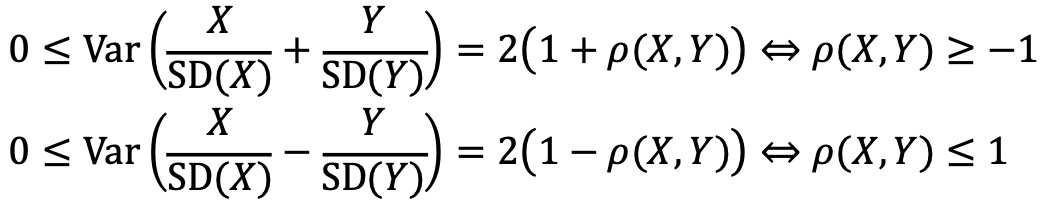
○ ρ(X, Y) = 1 : X와 Y는 완전 비례관계
○ ρ(X, Y) = -1 : X와 Y는 완전 반비례관계
○ ρ(X, Y) = 0이라고 X와 Y가 독립인 것은 아님
○ 반례 1. p(x) = ⅓ I{x = -1, 0, 1} , Y = X2
○ COV(X, Y) = E(XY) - E(X)E(Y) = E(XY) = E(X3) = 0
○ p(1, 1) = ⅓, p(x = 1) = ⅓, p(y = 1) = ⅔이므로, p(x, y) ≠ p(x) × p(y)
○ 독립의 정의 불성립
○ 반례 2. S ={(x, y) | -1 ≤ x ≤ 1, x2 ≤ y ≤ x2 + 1/10}, p = 5 I{(x, y) ∈ S}
○ COV(X, Y) = E(XY) - E(X)E(Y) = E(XY) = 0
○ 일정 = p(x, y) = p(x) × p(y)이라는 독립의 정의에서 p(x)는 일정하지만 p(y)는 일정하지 않음
○ 독립의 정의 불성립
⑤ 성질 2. ρ(X, X) = 1, ρ(X, -X) = -1
⑥ 성질 3. ρ(X, Y) = ρ(Y, X)
⑦ 성질 4. 크기 정보 제외 : ρ(aX + b, cY + d) = ρ(X, Y)
○ 유도 : ρ(aX + b, cY + d) = COV(aX + b, cY + d) ÷ aσx ÷ cσy = COV(X, Y) ÷ σxσy = ρ(X, Y)
⑧ 성질 5. 연관성 정보 : | ρ(X, Y) | = 1과 Y = aX + b, (a ≠ 0, b는 상수)는 필요충분조건
○ 정방향 증명 : Z 설정에 대한 아이디어는 단순회귀분석에서 유래
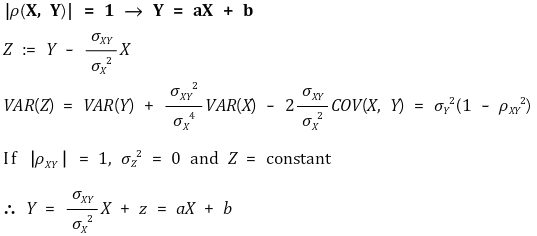
○ 역방향 증명
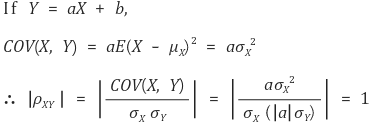
○ 귀무가설 H0 : 상관계수 = 0
○ 대립가설 H1 : 상관계수 ≠ 0
○ t 통계량 계산 : 표본으로부터 얻은 상관계수 r에 대하여,
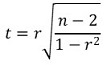
○ 위 통계량은 자유도가 n-2인 student t 분포를 따름 (단, 샘플의 개수를 n이라고 가정)
○ cor(x, y)
○ cor(x, y, method = "pearson")
○ cor.test(x, y)
○ cor.test(x, y, method = "pearson")
⑶ Spearman 상관계수(Spearman correlation coefficient)
① 정의 : x' = rank(x)와 y' = rank(y)에 대해 다음과 같이 정의
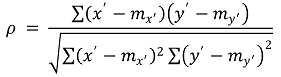
② 특징
○ 서열 척도인 두 변수들의 상관관계를 측정하는 방식
○ 순서형 변수를 대상으로 하는 비모수적 방법
○ 제로가 많은 데이터에 유리함
○ 데이터 내 편차나 에러에 민감
○ 켄달 상관계수보다 높은 값을 가짐
③ 성질 1. 두 다차원 변수의 rank 차이 d1, d2, ···에 대하여

④ 성질 2. 독립인 (X1, Y1), X2, Y3에 대하여

○ cor(x, y, method = "spearman")
○ cor.test(x, y, method = "spearman")
⑷ Kendall 상관계수(Kendall correlation coefficient)
① 정의 : concordant pair와 discordant pair에 대해 상관계수를 정의
② 특징
○ 서열 척도인 두 변수들의 상관관계를 측정하는 방식
○ 순서형 변수를 대상으로 하는 비모수적 방법
○ 제로가 많은 데이터에 유리함
○ 샘플 사이즈가 작거나 데이터의 동률이 많을 때 유용함
③ 절차
○ step 1. x 값에 대한 오름차순으로 y 값을 정렬 : 각 y 값을 yi로 표기
○ step 2. 각 yi 값에 대하여 yj > yi (단, j > i)인 concordant piar의 개수를 셈
○ step 3. 각 yi 값에 대하여 yj < yi (단, j > i)인 discordant pair의 개수를 셈
○ step 4. 상관계수 정의
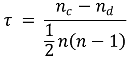
○ nc : total number of concordnat pairs
○ nd : total number of discordant pairs
○ n : size of x and y
○ 표본 Kendall 상관계수

○ cor(x, y, method = "kendall")
○ cor.test(x, y, method = "kendall")
⑸ Matthew correlation coefficient (MCC)

⑹ χ2 : 근사의 적합성을 나타내는 척도
① 측정데이터를 xm, ym, 근사함수를 f(x)라 하면

② 근사함수를 구할 때 χ2의 미분을 통한 극소점 계산을 거침
③ 2차 근사함수와 같은 비선형 회귀에서 사용
⑺ 에너지 통계량(energy statistics)
① 2007년 Székely, Rizzo, Bakirov이 제안
② 거리 공분산(distance covariance) V(X,Y)과 거리 상관계수(distance correlation) V(X,Y) / √V((X,X)·V(Y,Y))

4. Anscombe's Quartet [목차]
⑴ 평균, 표준편차, 상관계수로는 주어진 데이터의 개형을 설명할 수 없음을 보여줌
⑵ 예시 1
⑶ 예시 2
Figure. 2. Anscombe's Quartet
5. 순서통계량(order statistic) [목차]
⑴ 개요
① 가정 : Xi와 Xj는 독립
② 정의 : X1, ···, Xn을 재배열하여 Y1 < ··· < Yn이 되도록 Yi를 설정
⑵ 통계량
① 결합확률분포
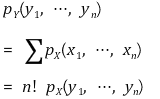
② 주변확률분포
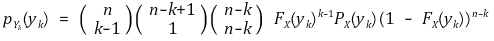
③ 기댓값
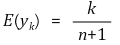
⑶ 순서통계량 예제
① 출제 유형 : n개 중 최댓값, 최솟값의 분포 및 통계량을 출제하거나 k번째 값의 분포를 출제
② 예제 1. 크기 3의 랜덤 샘플이 [0, 1]의 균등분포에서 추출되었습니다. 샘플의 최대값이 0.7보다 클 확률을 계산하세요.
○ 풀이
Pr(Y > 0.7) = 1 - (Pr(X ≤ 0.7))3 = 1 - 0.73 = 0.657
③ 예제 2. X는 평균이 1인 지수 분포를 따릅니다. 크기 3의 샘플이 추출되었습니다. 세 값 중 중간값의 기대값을 계산하세요.
○ 풀이
fY(x) = (3! / 1!1!1!)·(1 - e-x)·e-x·e-x = 6(e-2x - e-3x)
∴ E[Y] = ∫0 to ∞ 6x(e-2x - e-3x) dx = 5/6
6. 조건부 통계량 [목차]
⑴ 조건부 기댓값(conditional expectation)
① 정의
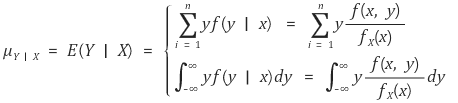
② 성질
○ E(XY | Y) = YE(X | Y)
○ E(aX1 + bX2 | Y) = aE(X1 | Y) + b(X2 | Y)
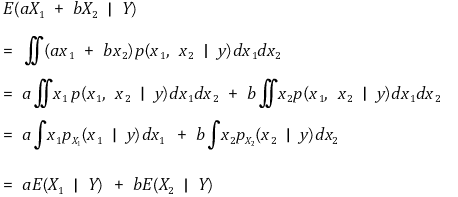
③ 반복 기댓값의 법칙(law of iterated expectation)
○ 정리

○ 증명
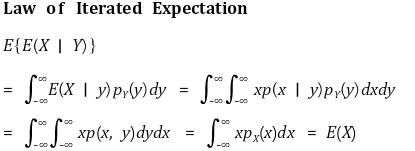
○ 예제
[0, ℓ]을 균일분포로 임의로 한 지점(Y)을 선택한 뒤, [0, y]을 균일분포로 임의로 한 지점(X)을 선택 시
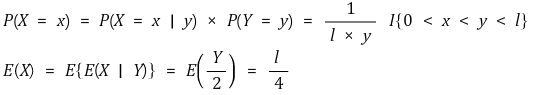
④ 평균독립(mean independence)
독립 ⊂ 평균독립 ⊂ 비상관성(uncorrelatedness)
○ 평균독립
○ 비상관성 : 상관계수가 0인 경우
○ (참고) 정규분포 : X와 Y가 jointly normal이고 uncorrelated이면 X와 Y는 독립
⑤ (참고) 단순회귀분석
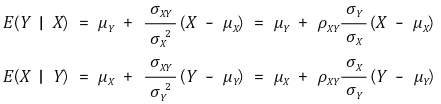
⑵ 조건부 분산(conditional variance)
① 정의 : 주어진 확률변수 X에 대해 Y의 조건부 분산
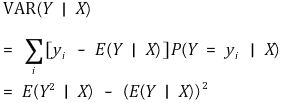
② 전분산의 정리(law of total variance, decomposition of variance)
○ 정리
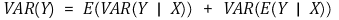
○ 증명

○ 의미
○ 상황 : X ~ P1(θ), Y ~ P2(X)일 때
○ VAR(Y | X), E(Y | X) 계산 시 P2를 이용
○ E{·}, VAR{·} 계산 시 P1을 이용
○ (참고) E(VAR(X | Y)) : 그룹 내 분산 (intra-group variance)
○ (참고) VAR(E(X | Y)) : 그룹 간 분산 (inter-group variance)
○ 예제 1.
○ X : 해고된 노동자의 실업기간
○ X의 확률밀도 : 지수분포
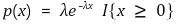
○ 전체 노동자의 20% : 숙련노동자. λ = 0.4
○ 전체 노동자의 80% : 미숙련노동자. λ = 0.1
○ VAR(X)의 계산

○ 예제 2.
○ 문제 : P를 자동차 보험을 갱신하는 가입자의 비율이라고 하자. P는 설계사에 따라 달라지며, 평균이 0.8이고 분산이 0.25인 베타 분포를 따른다. 보험 회사의 모든 가입자 중에서 10명을 선택한다고 하자. N은 자동차 보험을 갱신한 가입자의 수를 나타낸다. Var[N]을 계산하시오.
○ 풀이 : Var[N] = E[Var[N | P]] + Var[E[N | P]] = E[10P(1-P)] + Var[10P] = 10E[P] - 10E[P2] + 100Var[P] = 24.1
○ 제언 : P1, P2, ···, P10의 분포가 완전히 독립이 아니라 같은 분포에서 온 것이기 때문에 Var[N] ≠ ∑i Var[Pi]
입력: 2019.06.17 14:15
수정: 2025.01.12 11:02
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 7강. 연속확률분포 (1) | 2019.06.16 |
|---|---|
| 【통계학】 6강. 이산확률분포 (0) | 2019.06.16 |
| 【통계학】 4강. 확률변수와 분포 (0) | 2019.06.16 |
| 【통계학】 3강. 확률공간 (0) | 2019.06.16 |
| 【통계학】 12강. 오차해석 (오차이론) (0) | 2019.04.13 |






최근댓글