【통계학】 5-1강. 이미지 유사성 비교 : SSIM

5-1강. 이미지 유사성 비교 : SSIM

 

추천글 : 【통계학】 5강. 통계량 

---

1. 개요 [본문]

2. 이론 [본문]

3. 코드 [본문]

4. 출처 [본문]

---

 

1. 개요 [목차]

⑴ SSIM(structural similarity index measure)

⑵ 최초 소개 : Image Quality Assessment: From Error Visibility to Structural Similarity (2004, IEEE)

⑶ 기존 방법으로는 mean squared error를 조사하는 수준에 그쳤음

 

 

2. 이론 [목차]

⑴ 두 개의 이미지(image) 또는 윈도우(window) x와 y를 비교하는 상황에 대하여,

⑵ 이미지의 구성

① 휘도(luminance) : 빛의 밝기를 나타내는 양

 

 

② 대조(contrast) : 이미지 내에서 빛의 밝기가 극적으로 바뀌는 성질

 

 

③ 구조(structure) : 픽셀들의 상대적 위치가 만들어내는 성질

 

 

⑶ 비교 함수 

① 최종 비교 함수의 조건 : 최종 비교 함수를 S(x, y)라 했을 때, 

○ 조건 1. symmetry : S(x, y) = S(y, x)

○ 조건 2. S(x, y) ≤ 1

○ 조건 3. unique maximum : S(x, y) = 1 ⇔ x = y

② luminance comparison function 

○ 베버의 법칙(Weber's law)과 일관성이 있음

 

 

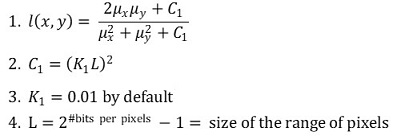
③ contrast comparison function

 

 

④ structure comparison function

○ 통계량 : σ_xx = var(x), σ_yy = var(y), σ_xy = cov(x, y)

 

 

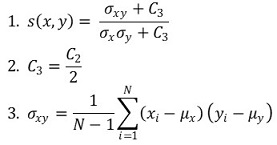
⑷ SSIM(mean structural similarity index)

① 수식화

 

 

 

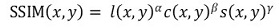
② default

 

 

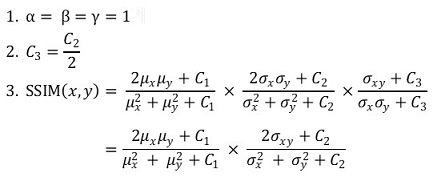
③ globally하게 쓰는 것보다 regionally하게 쓰는 게 더 효과 있음

○ 이유 1. 이미지의 통계적 특성 (예 : 평균, 분산) 등은 ROI에 따라 달라짐

○ 이유 2. 이미지 왜곡 또한 이미지 전반에 걸쳐 일정하지 않음

○ 이유 3. 사람의 시각 시스템도 이미지 전체가 아닌 일부분에만 집중된 점을 상기해야 함

○ 이유 4. regional하게 여러 가지 조합의 ROI를 분석할 수 있으므로 더 다양하고 풍성한 분석을 할 수 있음

 

 

3. 코드 [목차]

 

def SSIM(x, y):
    # assumption : x and y are grayscale images with the same dimension

    import numpy as np
    
    def mean(img):
        return np.mean(img)
        
    def sigma(img):
        return np.std(img)
    
    def cov(img1, img2):
        img1_ = np.array(img1[:,:], dtype=np.float64)
        img2_ = np.array(img2[:,:], dtype=np.float64)
                        
        return np.mean(img1_ * img2_) - mean(img1) * mean(img2)
    
    K1 = 0.01
    K2 = 0.03
    L = 256 # when each pixel spans 0 to 255
   
    C1 = K1 * K1 * L * L
    C2 = K2 * K2 * L * L
    C3 = C2 / 2
        
    l = (2 * mean(x) * mean(y) + C1) / (mean(x)**2 + mean(y)**2 + C1)
    c = (2 * sigma(x) * sigma(y) + C2) / (sigma(x)**2 + sigma(y)**2 + C2)
    s = (cov(x, y) + C3) / (sigma(x) * sigma(y) + C3)
        
    return l * c * s

 

⑴ 파이썬에서 함수 사용하는 법 

 

 

4. 출처 [목차]

⑴ https://medium.com/srm-mic/all-about-structural-similarity-index-ssim-theory-code-in-pytorch-6551b455541e

All about Structural Similarity Index (SSIM): Theory + Code in PyTorch

⑵ https://en.wikipedia.org/wiki/Structural_similarity

Structural similarity - Wikipedia

 

입력: 2021.02.19 21:04