통계학 요점 정리
추천글 : 【통계학】 통계학 목차
1. 데이터, 정보, 지식
⑴ 데이터 : 주어진 자료
⑵ 정보 : 데이터의 이름
⑶ 지식 : 정보와 정보의 관계
2. 비율척도, 구간척도, 순서척도, 명목척도
⑴ 비율척도 : 절대영점 존재. 비율 개념 존재. 절대영도 등
⑵ 구간척도 : 절대영점 부존재. 비율 개념 부존재. 섭씨온도 등
⑶ 순서척도 : 순서 개념
⑷ 명목척도 : 성별 등
3. 가설연역법과 데이터 과학의 차이점
⑴ 가설연역법은 선 가설설정 후 실험
⑵ 데이터 과학은 선 실험 후 가설설정
4. 정확도와 정밀도
⑴ 정확도는 표본평균이 모평균에 얼마나 가까운지에 대한 개념
⑵ 정밀도는 표본의 분산이 얼마나 작은지에 대한 개념
5. 교락효과
⑴ 제3의 요인이 조작변인과 종속변인에 모두 영향을 미치는 것
⑵ 상관관계가 인과관계를 의미하지 않는 이유
6. batch effect의 의미
⑴ 올바르지 못한 반복실험
⑵ batch에 가해지는 통제변인이 제대로 통제되지 못해 잘못된 통계적 결론이 유도되는 것
7. 측정실험과 조작실험의 의미
⑴ 측정실험은 실험자가 조건을 바꾸지 않고 가설을 검정하는 것. 데이터 과학에 적용
⑵ 조작실험은 실험자가 조건을 바꿔서 가설을 검정하는 것. 일반적인 과학적 방법론에 적용
8. 반복실험과 반복측정의 차이
⑴ 반복실험은 정확도와 관련된 개념. 신약 검정에서 여러 환자들을 테스트하는 것
⑵ 반복측정은 정밀도와 관련된 개념. 신약 검정에서 동일 환자를 여러 번 테스트하는 것
9. mean, median 비교
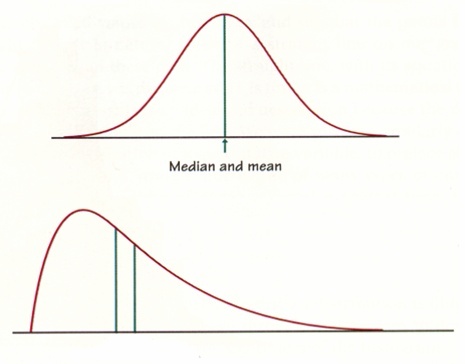
⑴ 왼쪽이 median, 오른쪽이 mean
⑵ median을 기준으로 양쪽의 넓이가 같아야 함
10. 분위수 대 분위수 그래프
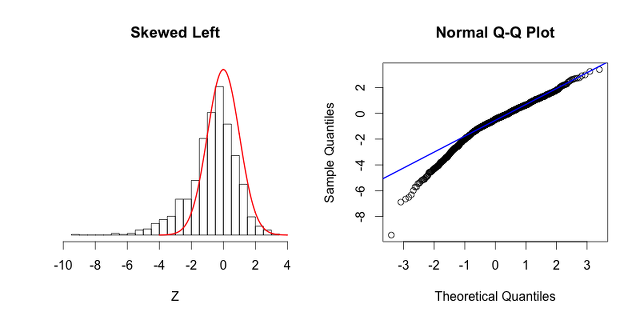
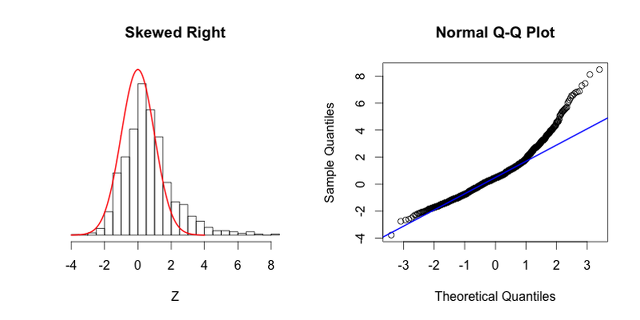
11. 독립의 의미
⑴ 한 변수에 대한 정보가 다른 변수에 대한 어떤 정보도 제공하지 않는 것
⑵ P(X = x, Y = y) = P(X = x) × P(Y = y)
12. 중심극한법칙
모집단의 분포와 관계없이 표본평균의 분포는 정규분포를 따름
13. chi-square goodness-of-fit test
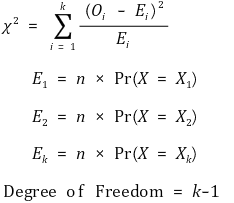
14. chi-square independence test

15. t 분포의 특징
⑴ 표준정규분포보다 뚱뚱함
16. 대립가설을 정할 때 주의사항
⑴ 반증가능성이 있어야 함
17. parametic testing과 non-parametic testing
⑴ parametic testing
① 일반적으로 표본들의 분포가 정규분포를 따르는 경우
② parameter를 통해 p-value 계산
⑵ non-parametic testing
① 일반적으로 표본들의 분포가 정규분포를 따르지 않는 경우
② parameter 없이 p-value 계산
18. 단측검정을 하는 이유
⑴ 상황 : 한쪽이 아니라는 자기 확신이 있을 때
⑵ 장점 : 제2종 오류를 줄일 수 있음
① 제2종 오류 : 대립가설이 참일 때 귀무가설을 채택하는 오류
② 실험자 입장에서 원하는 결론을 볼 가능성이 있음
⑶ 단점 1. 잘못된 통계적 결론을 낼 수 있음 : p-value가 underestimate됨
⑷ 단점 2. 자기 확신에 대한 설득을 해야 함
19. 실험설계 : 신발 실험
⑴ 왼쪽 신발과 오른쪽 신발은 형태와 용례가 많이 다른데 이를 어떻게 비교할 것인지가 문제가 됨
20. 실험설계
⑴ 문제 : genetic diversity group에 실험하는 게 맞는지 아니면 genetic unified group에 실험하는 게 맞는지
⑵ 답안 : genetic diversity group
① 실제로 임상에서 적용되는 상황은 genetic diversity group임 : genetic unified group에서 얻어진 결론의 실효성 문제
② 사후검정을 통해 genetic diversity group에서 유의미한 결론을 얻을 수 있음 : 이후 가설연역법 적용
21. 검정력
⑴ 검정력을 높이는 것은 α가 일정할 때 p value가 더 작게 나오는 통계 기법을 사용한다는 의미
⑵ 예 1. t 분포는 자유도가 높을수록 검정력이 높음
① 자유도가 높을수록 t 분포는 정규분포와 유사해짐
② 자유도가 높을수록 t 분포의 폭이 좁아져서 검정력이 높아짐
⑶ 예 2. 대응표본검정보다 이표본검정의 검정력이 높음
① 대응표본검정 : 사실상 변수가 하나임. 자유도는 n-1
② 이표본검정 : 변수가 두 개임. 자유도는 n+m-2
③ t 분포에서 자유도가 증가하면 검정력이 늘어나므로 이표본 검정의 검정력이 높음
⑷ 예 3. 이표본검정 중 등분산 가정이 없을 때보다 등분산 가정이 있을 때 검정력이 높음
① 등분산 가정이 있을 때 자유도
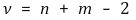
② 등분산 가정이 없을 때 자유도
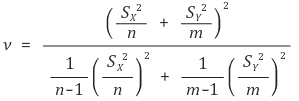
⑸ 예 4. 회귀분석에서 t 검정보다 F 검정이 검정력이 더 높음
⑹ 예 5. 평행성을 만족하는 자료에서 각 회귀선의 y절편을 비교하는 것보다 ANCOVA를 하는 게 검정력이 높음
① y 절편의 비교는 샘플 사이즈가 한 표본집단의 샘플 사이즈 수준
② ANCOVA는 전체 에러 텀을 가지고 계산하므로 샘플 사이즈가 한 표본집단의 샘플 사이즈의 두 배 수준
22. 여러 개의 집단이 있을 때 pairwise t-test를 하면 안 되는 이유
제1종 오류의 누적으로 인해 별로 차이가 나지 않는 두 그룹에도 차이가 난다고 결론지을 가능성이 높음
23. ANOVA 분석의 가정
⑴ 정규성 : 모든 데이터는 정규분포를 따르는 모집단들로부터 추출됨
⑵ 독립성 : 모든 데이터는 모집단들로부터 독립적으로 추출됨
⑶ 등분산성 : 모든 데이터는 평균이 달라도 분산은 동일한 모집단들로부터 추출됨
24. 강건성의 의미
많은 샘플수, 카테고리 내 동일 반복수 등을 만족 시 이분산성, 비정규성에서도 통계적 결론(귀무가설을 인용하거나 기각)이 달라지지 않는 것
25. 선형상관의 가정
⑴ 임의 추출된 자료
⑵ 각 변수는 정규분포를 따르는 모집단에서 추출됐을 것
⑶ 관계가 선형으로 나타남
26. 상관관계와 회귀분석의 차이점
⑴ 상관관계는 단순히 변수들간의 관계의 정도를 나타낸 것
⑵ 회귀분석은 종속변수에 대한 독립변수의 인과관계를 나타낸 것. 예측이 목적이기 때문에 실제 인과관계를 입증하지 않아도 됨
27. 회귀모형의 가정
⑴ Y값은 정규성과 등분산성을 만족하는 모집단으로부터 측정된 것으로 가정
⑵ 독립변수 X는 오차 없이 측정되었다고 가정 : 실제적으로 만족하기 어려움
⑶ 종속변수는 독립변수에 의해서 결정된다고 가정
⑷ X와 Y의 관계가 선형이라는 가정
28. 다중공선성의 의미
다중선형회귀분석에서 둘 또는 그 이상의 독립변수가 강한 상관관계를 갖는 것. 각 회귀변수의 계수의 표준오차가 커지는 문제를 낳는다.
29. ANCOVA의 가정
⑴ 등분산성(homoscedasticity)
⑵ 독립성(independency)
⑶ 정규성(normality)
⑷ 공변량(covariate)과 종속변수의 관계가 선형일 것
⑸ 평행성(parallelism)
30. ANCOVA의 과정
⑴ 1st. 독립변수와 공변량의 상호작용이 통계적으로 유의하지 않음을 확인
⑵ 2nd. 종속변수에 대한 공변량의 회귀선을 계산
⑶ 3rd. 그 회귀선으로부터 y절편을 변경하여 각 독립변수의 level에서 제곱합이 최소가 되도록 하는 회귀선들을 계산
⑷ 4th. 각 level의 회귀선으로부터 그 level 내 데이터들의 잔차들을 계산
⑸ 5th. 전체 집단에 대한 공변량의 평균을 구한 뒤 그 값에 대한 각 회귀선의 함수값을 표준값으로 지정
⑹ 6th. 각 level에 대해 표준값에서 앞서 구한 잔차들을 위아래로 표시
⑺ 7th. 보정된 데이터 하에서 ANOVA를 수행
31. 평행성의 의미
⑴ 예를 들면 오염된 광산 지역과 그렇지 않은 지역 각각의 회귀선을 계산 시 기울기가 같을 것을 지칭
⑵ 만일 평행성이 만족하지 않으면 하나의 선택된 값(예 : 나이의 전체 평균)에 대해 차이를 비교하는 것은 공변량의 범위 전체를 대표할 수 없음
32. 머신러닝에서 오버피팅을 시키면 안되는 이유
⑴ 오버피팅을 시키면 표본의 부정확성까지 학습을 하여 예측확률이 떨어짐
⑵ 실제 머신러닝에서는 매 스텝마다 에러를 의도적으로 입력함
입력 : 2019.12.10 00:07
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 전하는 말 (0) | 2020.03.24 |
|---|---|
| 【통계학】 20강. 회귀분석의 분산분석 (0) | 2019.12.07 |
| 【통계학】 19강. 고급 회귀분석 (0) | 2019.11.26 |
| 【통계학】 16강. 선형 회귀분석 (0) | 2019.11.24 |
| 【통계학】 1-1강. 분위수 대 분위수 플롯(Q-Q plot) (0) | 2019.10.10 |




최근댓글