19강. 고급 회귀분석
추천글 : 【통계학】 통계학 목차
1. 타당도 [본문]
2. 패널 데이터 [본문]
3. 도구 변수 [본문]
4. 랜덤 통제 실험 [본문]
5. 유사실험 [본문]
6. heterogeneous population [본문]
1. 타당도(validity) [목차]
⑴ 내부적 타당도(internal validity)
① 정의 : 회귀분석 결과 얻은 각 계수가 타당하게 계산된 것인지에 대한 정성적 평가
② 위협 요인 1. omitted variable bias
○ 정의 : 다음 두 가지 조건을 만족하는 변수가 존재하는 경우 잔차의 기댓값이 0이 아니게 되는 것
○ 조건 1. 하나 또는 몇 개의 기존 변수들과 상관관계가 있을 것
○ 조건 2. 생략된 변수가 Y의 결정자(determinator)일 것
○ 잔차의 기댓값 예시

○ 해결방법
○ omitted variable을 회귀분석 시에 포함
○ 만일 해당 omitted variable에 관한 데이터가 없는 경우 다음 3가지 방법이 존재함
○ 방법 1. 패널 데이터(panel data) : 시간에 따라 변하지 않는 특성인 경우 제거 가능
○ 방법 2. 도구변수 회귀(instrumental variable regression) : 도구변수를 통해 에센스 정보만 추출할 수 있음
○ 방법 3. 랜덤 통제 실험 하에서 새롭게 정보를 수집하는 방법
③ 위협 요인 2. wrong functional form bias
○ 정의 : 비선형 관계에 선형회귀분석을 함으로써 생기는 바이어스
○ omitted variable bias의 일종
④ 위협 요인 3. errors-in-variable bias 또는 measurement error in the regressors
○ 정의 : 측정오차가 있는 독립변수 X̃i 는 오차 vi와 상관관계를 보일 수 있음
○ 수식화
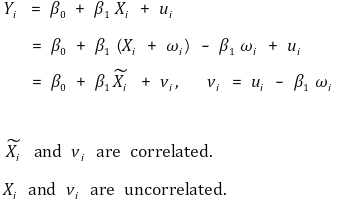
○ 문제점 1. 계량경제학의 철의 법칙(the iron law of econometrics) : 기울기의 OLS 추정량은 참값보다 낮아지는 경향이 있음
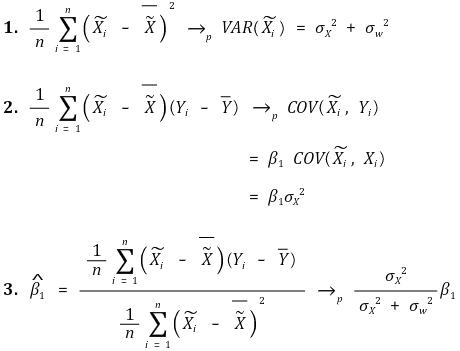
○ 문제점 2. OLS 추정량이 일관성(consistency)이 없음
○ 문제점 3. 통계적 추론이 부정확함
○ 해결방법
○ 방법 1. 측정기기의 정확도 향상
○ 방법 2. 도구변수 회귀 : 도구변수를 통해 에센스 정보만 추출할 수 있음
○ 방법 3. 오차 보정 : 오차가 패턴이 있는 경우 보정 가능
○ (참고) 종속변수에 측정오차가 있는 경우
○ 수식화
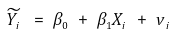
○ 기울기의 추정량은 변하지 않음
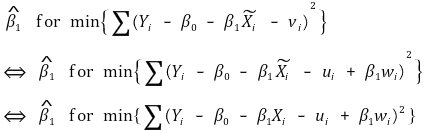
○ 단순선형회귀모델의 3대 가정을 만족
○ 가정 1. Xi가 vi에 대한 어떤 정보도 제공하지 않음
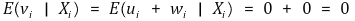
○ 가정 2.
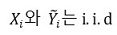
○ Yi와 wi는 i.i.d.이고 상호독립이기 때문에 Ỹi 는 i.i.d.
○ i ≠ j에 대해 Xi는 Yj 및 wj와 독립이기 때문에 Xi와 Ỹi 는 독립
○ 따라서 가정 2를 만족함
○ 가정 3. 4차 적률(4th order moment)의 존재성
○ ui와 wi는 유한한 4차 적률을 가지고 상호독립이기 때문에 vi = ui + wi는 유한한 4차 적률을 가짐
○ 따라서 (Xi, vi)는 0이 아닌 유한한 4차 적률을 가짐
○ errors-in-variable bias의 경우와 3가지 차이점이 존재
○ 차이 1. OLS 추정량이 일관성(consistency)이 있음
○ 차이 2. 통계적 추론이 정확함
○ 차이 3. 회귀 에러의 분산을 증가시킴 → OLS 추정량의 분산도 증가
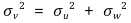
⑤ 위협 요인 4. sample selection bias
○ 데이터 선택 과정에서 바이어스가 생기는 경우
○ 즉, 전체 집단의 특성을 추론할 때 부분으로부터 추론하여 바이어스가 생기는 경우
○ 예 1. 요인 A와 요인 B에 대한 채용률
○ 채용률은 A와 B가 증가할수록 증가한다고 가정
○ A 요인이 낮은 사람들은 지원 자체를 안 하려고 함
○ A 요인이 낮은 사람들 중 B 요인이 높은 사람들이 지원을 함
○ 그 결과 A 요인에 대한 채용률 회귀곡선에서 A 요인에 대한 효과가 실제보다 낮게 측정
⑥ 위협 요인 5. simultaneous causality bias
○ 독립변수에서 종속변수로 causal link가 있는 것은 당연함
○ 종속변수에서 독립변수로 causal link가 있는 경우 위 독립변수의 계수에 바이어스가 발생
○ 마치 피드백 회로가 복잡한 수식으로 표현되는 것을 상기하면 됨
○ 양성 피드백 회로 : 계수의 절대값을 크게 함
○ 음성 피드백 회로 : 계수의 절대값을 작게 함
○ 예 : 출생률과 사망률은 양방향 인과관계가 있음. 양성 피드백 회로와 유사
○ 해결방법
○ 방법 1. 도구변수 회귀 : causal link가 제거된 에센스 정보만을 추출
○ 방법 2. 랜덤 통제 실험 : 랜덤하게 treatment를 처리함으로써 종속변수의 인과성을 제거
⑵ 외부적 타당도(external validity)
① 정의 : 회귀분석 결과 얻은 각 독립변수의 계수를 다른 모집단에서도 적용할 수 있는지에 대한 정성적 평가
② 위협 요인 1. 대표성이 없는 샘플(non-representative sample) : 모집단 자체의 차이
③ 위협 요인 2. 대표성이 없는 프로그램 또는 정책(non-representative program or policy) : 시스템의 차이
○ 모집단이 같아도 시스템이 달라서 외부적 타당도 위반이 될 수 있음
○ 예 : 교육환경의 차이, 법 및 제도의 차이, 물리적 환경의 차이
④ 위협 요인 3. general equilibrium effect
○ 정의 : treatment로 인해 전체 환경이 바뀌고 이로 인해 treatment의 효과가 증폭되거나 억제될 수 있음
○ simultaneous causality bias와 유사함
○ 예시 : 석유 유전의 존재가 소득에 미치는 영향
○ 유전의 존재 → 근로자들의 소득 증가
○ 근로자들의 소득 증가 → 새로운 근로자들의 유입 증가
○ 주택 구입률 증가 → 주택 부족으로 인한 주택 가격 증가 → 소득 감소 요인
○ 자동차 혼잡도 증가 → 소득 감소 요인
○ 소득 증가에 따른 식당 품질증가의 요구 증가 → 외식비 증가 → 소득 감소 요인
⑤ 해결방법
○ 모집단과 셋팅에 따라 회귀관계의 결론을 조절하는 방법
○ 메타분석(meta-analysis) : 같지는 않지만 비슷한 모집단들의 결론을 비교해 보는 것
2. 패널 데이터(panel data) [목차]
⑴ 개요
① 다음과 같은 데이터를 지칭

② 균형 패널 데이터(balanced panel data) : 모든 시간 구간에서 모든 엔티티가 갖춰진 경우
③ 비균형 패널 데이터(unbalanced panel data) : 균형 패널 데이터가 아닌 경우
④ (구별개념) repeated cross-sectional data
○ 패널 데이터는 각각의 개인에 대해 추적한 데이터
○ repeated cross-sectional data는 시간을 달리하여 얻은 데이터
○ repeated cross-sectional data에도 동일인이 전후 데이터에 포함될 수 있고 저렴함
⑵ before and after regression model
① 수식화
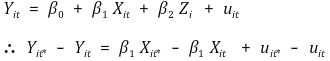
○ 시간에 따라 상수인 요소를 제거할 수 있음
○ Z는 i에 따라 다른 값을 가지므로 intercept와 차이가 있음
② fixed effect regression model의 일종
⑶ fixed effect regression model
① 주요 가정
○ 가정 1. E(uit | Xi1, ···, XiT, αi) = 0 : E(uit | Xit, αi) = 0으로는 충분하지 않음 (∵ Y와 u의 평균치에 모든 시간의 정보가 쓰임)
○ 가정 2. (Xi1, ···, XiT, ui1, ···, uiT)는 결합분포 하에서 i.i.d. : 즉, cov(uit, uis) = 0 (t ≠ s)을 의미하는 게 아님
○ 가정 3. 4차 적률의 존재성
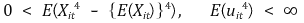
○ 가정 4. 완전 다중공선성이 없을 것 : Xit는 반드시 t에 따라 달라야 함
○ 주요 가정 하에 fixed effect estimator는 일관성(consistency)과 정규근사성(asymptotically normality)을 만족
○ n과 T는 무관하므로 n이 무한으로 커져도 Y의 시간평균은 일관성과 정규근사성을 만족하지 않음
② 수식화
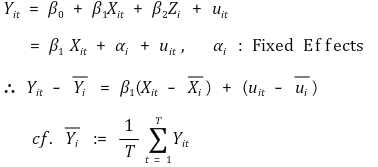
○ 데이터를 i에 관한 축과 t에 관한 축 상에서 표현되는 테이블로 이해해야 함
○ T = 2인 경우 before and after regression model에 해당
○ slope 표준편차 = clustered standard error = HAC(heteroscedasticity & autocorrelation consistent standard error)
○ t = 1, ···, T까지 총 T개의 회귀선이 나오는 게 아님. 그저 한 개의 회귀선에 불과
○ β1이지 β1, t가 아님
③ 알고리즘 예시
data <- read.csv("C:/Users/sun/Desktop/Guns.csv", header = T)
attach(data)
y <- data[, 2]
y <- log(y)
x1 <- data[, 13]
x2 <- data[, 5]
x3 <- data[, 11]
x4 <- data[, 10]
x5 <- data[, 9]
x6 <- data[, 6]
x7 <- data[, 7]
x8 <- data[, 8]
state_y <- array(dim = 56)
state_x1 <- array(dim = 56)
state_x2 <- array(dim = 56)
state_x3 <- array(dim = 56)
state_x4 <- array(dim = 56)
state_x5 <- array(dim = 56)
state_x6 <- array(dim = 56)
state_x7 <- array(dim = 56)
state_x8 <- array(dim = 56)
for(i in 1:56){
if(i != 3 && i != 7 && i != 14 && i != 43 && i != 52){
data_sub <- data[stateid == i, ]
state_y[i] <- mean(data_sub[, 2])
state_x1[i] <- mean(data_sub[, 13])
state_x2[i] <- mean(data_sub[, 5])
state_x3[i] <- mean(data_sub[, 11])
state_x4[i] <- mean(data_sub[, 10])
state_x5[i] <- mean(data_sub[, 9])
state_x6[i] <- mean(data_sub[, 6])
state_x7[i] <- mean(data_sub[, 7])
state_x8[i] <- mean(data_sub[, 8])
}
}
Y <- array(dim = 1173)
X1 <- array(dim = 1173)
X2 <- array(dim = 1173)
X3 <- array(dim = 1173)
X4 <- array(dim = 1173)
X5 <- array(dim = 1173)
X6 <- array(dim = 1173)
X7 <- array(dim = 1173)
X8 <- array(dim = 1173)
for(i in 1 : dim(data)[1]){
j <- data[i, 12]
Y[i] <- y[i] - state_y[j]
X1[i] <- x1[i] - state_x1[j]
X2[i] <- x2[i] - state_x2[j]
X3[i] <- x3[i] - state_x3[j]
X4[i] <- x4[i] - state_x4[j]
X5[i] <- x5[i] - state_x5[j]
X6[i] <- x6[i] - state_x6[j]
X7[i] <- x7[i] - state_x7[j]
X8[i] <- x8[i] - state_x8[j]
}
RELATION <- lm(Y ~ X1 + X2 + X3 + X4 + X5 + X6 + X7 + X8)
summary(RELATION)
④ fixed effect regression model 적용 결과 원래 결과와 크게 다른 결론이 나온 경우
○ 원래 모델에서 omitted variable bias가 있었음을 강력히 시사
⑤ 주요 가정을 만족해도 자기상관이 있을 수 있음
○ 자기상관(autocorrelation) : uit와 uit* (t ≠ t*)도 serial correlation이 있을 수 있음. HAC와 관련
○ 자기상관이 없는 경우

○ 자기상관이 있는 경우

○ 자기상관이 없는 경우 cov(vit, vis) = 0 (단, k ≠ s)의 증명
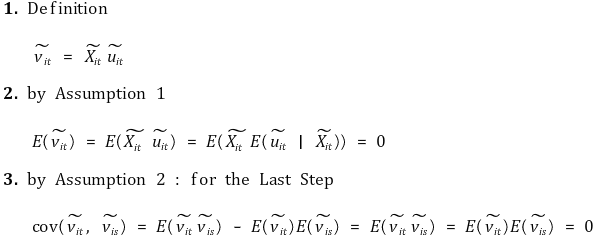
⑷ fixed effect regression model 행렬 표현
① 모델링
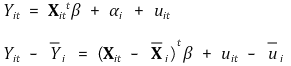
② 가정

③ fixed effects estimator
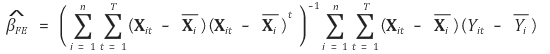
④ consistency
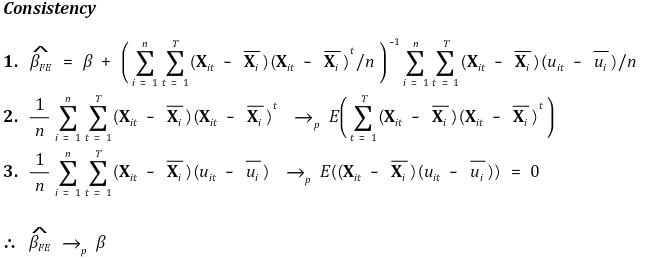
⑤ asymptotic normality
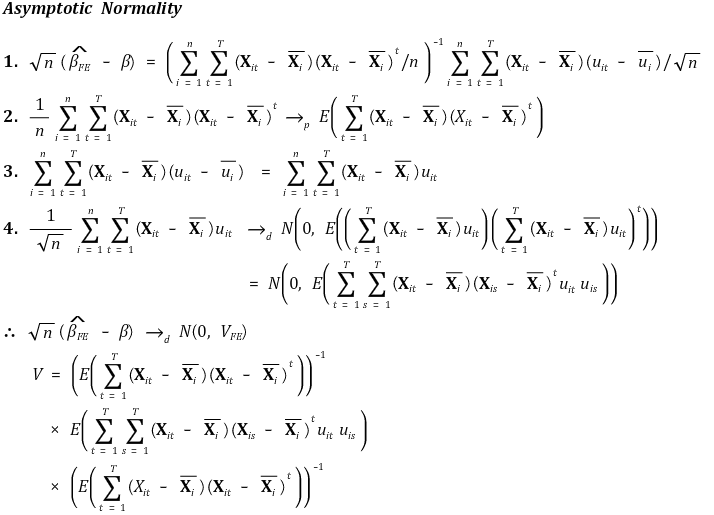
⑸ LSDV(least squares dummy variables model)
① 수식화
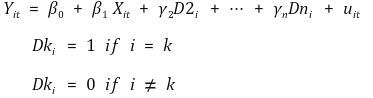
② D1i를 포함시키지 않은 이유 : 완전 다중공선성(perfect multi-collinearity)을 피하기 위함
○ 수식화
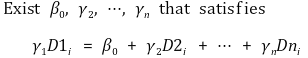
○ 저런 계수들이 존재하면 γ1이 얼마가 되도 상관 없음 : 즉 γ1을 정의할 수 없음
○ 더미변수가 야기하는 완전 다중공선성을 더미 변수 트랩(dummy variable trap)이라고도 함
③ i의 범위 n이 너무 커지면 계산 불가능 : 회귀변수의 개수가 너무 많아지므로
⑹ 시간효과(time effect)
① 시간효과 항(time effect term) : λt로 표시
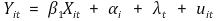
② 모델링
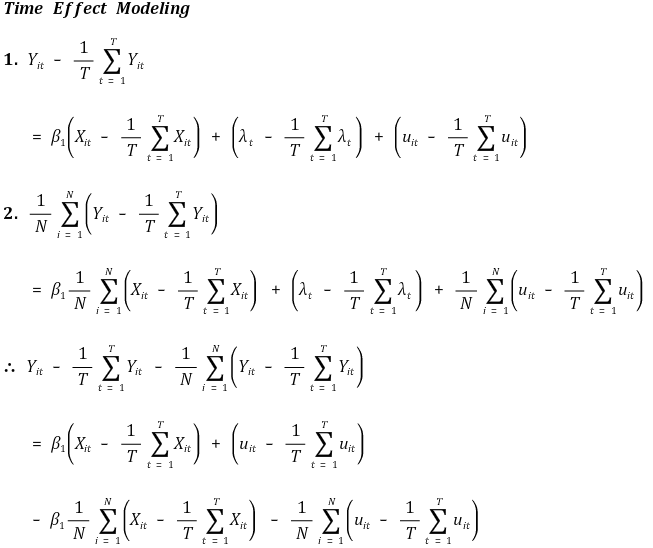
③ 알고리즘 예시
data <- read.csv("C:/Users/sun/Desktop/Guns.csv", header = T)
attach(data)
# definition
y <- data[, 2]
y <- log(y)
x1 <- data[, 13]
x2 <- data[, 5]
x3 <- data[, 11]
x4 <- data[, 10]
x5 <- data[, 9]
x6 <- data[, 6]
x7 <- data[, 7]
x8 <- data[, 8]
# elimination of fixed state effects
state_y <- array(dim = 56)
state_x1 <- array(dim = 56)
state_x2 <- array(dim = 56)
state_x3 <- array(dim = 56)
state_x4 <- array(dim = 56)
state_x5 <- array(dim = 56)
state_x6 <- array(dim = 56)
state_x7 <- array(dim = 56)
state_x8 <- array(dim = 56)
for(i in 1:56){
if(i != 3 && i != 7 && i != 14 && i != 43 && i != 52){
data_sub <- data[stateid == i, ]
state_y[i] <- mean(data_sub[, 2])
state_x1[i] <- mean(data_sub[, 13])
state_x2[i] <- mean(data_sub[, 5])
state_x3[i] <- mean(data_sub[, 11])
state_x4[i] <- mean(data_sub[, 10])
state_x5[i] <- mean(data_sub[, 9])
state_x6[i] <- mean(data_sub[, 6])
state_x7[i] <- mean(data_sub[, 7])
state_x8[i] <- mean(data_sub[, 8])
}
}
Y <- array(dim = 1173)
X1 <- array(dim = 1173)
X2 <- array(dim = 1173)
X3 <- array(dim = 1173)
X4 <- array(dim = 1173)
X5 <- array(dim = 1173)
X6 <- array(dim = 1173)
X7 <- array(dim = 1173)
X8 <- array(dim = 1173)
for(i in 1 : dim(data)[1]){
j <- data[i, 12]
Y[i] <- y[i] - state_y[j]
X1[i] <- x1[i] - state_x1[j]
X2[i] <- x2[i] - state_x2[j]
X3[i] <- x3[i] - state_x3[j]
X4[i] <- x4[i] - state_x4[j]
X5[i] <- x5[i] - state_x5[j]
X6[i] <- x6[i] - state_x6[j]
X7[i] <- x7[i] - state_x7[j]
X8[i] <- x8[i] - state_x8[j]
}
# elimination of fixed time effects
time_Y <- array(dim = 23)
time_X1 <- array(dim = 23)
time_X2 <- array(dim = 23)
time_X3 <- array(dim = 23)
time_X4 <- array(dim = 23)
time_X5 <- array(dim = 23)
time_X6 <- array(dim = 23)
time_X7 <- array(dim = 23)
time_X8 <- array(dim = 23)
for(t in 77:99){
data_sub2 <- data[year == t, ]
time_Y[t - 76] <- mean(data_sub2[, 2]) - mean(state_y, na.rm = TRUE)
time_X1[t - 76] <- mean(data_sub2[, 13]) - mean(state_x1, na.rm = TRUE)
time_X2[t - 76] <- mean(data_sub2[, 5]) - mean(state_x2, na.rm = TRUE)
time_X3[t - 76] <- mean(data_sub2[, 11]) - mean(state_x3, na.rm = TRUE)
time_X4[t - 76] <- mean(data_sub2[, 10]) - mean(state_x4, na.rm = TRUE)
time_X5[t - 76] <- mean(data_sub2[, 9]) - mean(state_x5, na.rm = TRUE)
time_X6[t - 76] <- mean(data_sub2[, 6]) - mean(state_x6, na.rm = TRUE)
time_X7[t - 76] <- mean(data_sub2[, 7]) - mean(state_x7, na.rm = TRUE)
time_X8[t - 76] <- mean(data_sub2[, 8]) - mean(state_x8, na.rm = TRUE)
}
YY <- array(dim = 1173)
XX1 <- array(dim = 1173)
XX2 <- array(dim = 1173)
XX3 <- array(dim = 1173)
XX4 <- array(dim = 1173)
XX5 <- array(dim = 1173)
XX6 <- array(dim = 1173)
XX7 <- array(dim = 1173)
XX8 <- array(dim = 1173)
for(i in 1 : dim(data)[1]){
j <- data[i, 1]
YY[i] <- Y[i] - time_Y[j - 76]
XX1[i] <- X1[i] - time_X1[j - 76]
XX2[i] <- X2[i] - time_X2[j - 76]
XX3[i] <- X3[i] - time_X3[j - 76]
XX4[i] <- X4[i] - time_X4[j - 76]
XX5[i] <- X5[i] - time_X5[j - 76]
XX6[i] <- X6[i] - time_X6[j - 76]
XX7[i] <- X7[i] - time_X7[j - 76]
XX8[i] <- X8[i] - time_X8[j - 76]
}
RELATION <- lm(YY ~ XX1 + XX2 + XX3 + XX4 + XX5 + XX6 + XX7 + XX8)
summary(RELATION)
⑺ 더미 변수(dummy variable)를 이용한 시간 효과 회귀
① 수식화
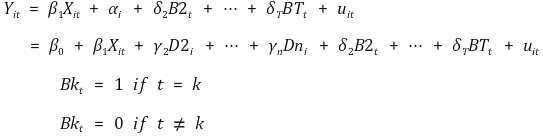
② B1t를 포함시키지 않은 이유 : 완전 다중공선성(perfect multi-collinearity)을 피하기 위함
○ 수식화
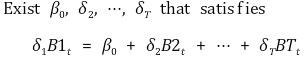
○ 저런 계수들이 존재하면 δ1이 얼마가 되도 상관 없음 : 즉 δ1을 정의할 수 없음
○ 더미변수가 야기하는 완전 다중공선성을 더미 변수 트랩(dummy variable trap)이라고도 함
3. 도구변수(instrumental variable) [목차]
⑴ 정의 : 제3의 변수로 회귀변수의 에센스(essence)만을 분리하는 방법
⑵ 단순표현
① 모델링
○ 회귀변수가 하나인 경우
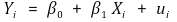
○ 회귀변수가 다중인 경우
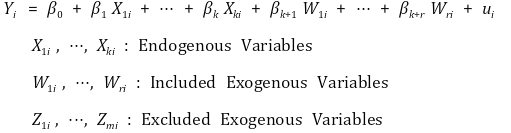
○ endogenous variable : ui와 상관관계가 있는 변수
○ exogenous variable : ui와 상관관계가 없는 변수
○ exactly identified : m = k
○ over-identified : m > k
○ under-identified : m < k
○ under-identified에서 모델링 불가 : 도구변수가 많아야 한다는 의미
○ W를 포함시킨 이유 : 조건을 만족하는 Z를 찾기 어려울 때 이를 가능케 함
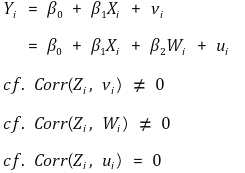
② 가정 : 도구변수 회귀를 쓰기 위한 가정
○ 가정 1. E(ui | W1i, ···, Wri) = 0
○ 가정 2. (X1i, ···, Xki, W1i, ···, Wri, Z1i, ···, Zmi, Yi)는 i.i.d.
○ 가정 3. 모든 변수는 유한한 4차 적률을 가짐
○ 가정 4. 도구변수 유효성
○ 4-1. instrument relevance
○ 4-2. instrument exogeneity
○ 4-3. no perfectly collinearity
○ 이 가정이 만족하면 TSLS 추정량은 일관성과 정규근사성을 만족
③ 과정
○ 회귀변수가 하나인 경우
○ 1st. Xi를 도구변수 Zi로 회귀
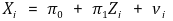
○ 2nd. Xi의 추정량을 계산
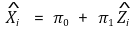
○ 3rd. Yi를 Xi의 추정량으로 회귀
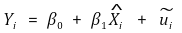
○ 회귀변수가 여럿인 경우
○ 1st. Xi를 도구변수 Zi로 회귀 : ℓ = 1, ···, k에 대하여
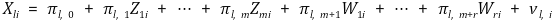
○ 2nd. Xi의 추정량을 계산 : ℓ = 1, ···, k에 대하여
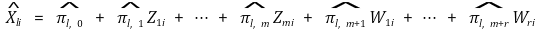
○ 3rd. Yi를 Xi의 추정량으로 회귀 : ℓ = 1, ···, k에 대하여
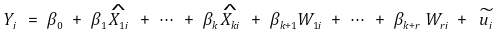
○ OLS 회귀를 두 번 하는 것은 표준 에러를 잘못 계산할 우려가 있음
④ TSLS(two-step least squares) 추정량
○ 수식화
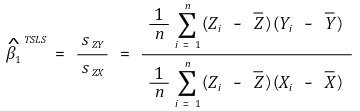
○ 증명

○ (참고) Zi := Xi라면 β1의 TSLS 추정량은 β1의 OLS 추정량과 동일함
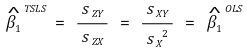
⑤ 일관성(consistency)
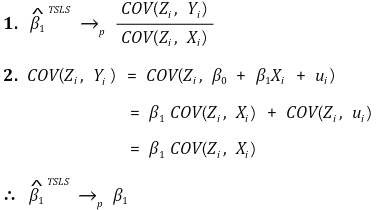
⑥ 정규근사성(asymptotic normality)
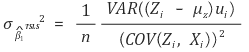
⑶ 도구변수 유효성 보충
① instrument relevance
○ 수식화
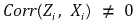
○ 약한 도구변수 : 회귀변수와 충분한 상관관계가 있지 않는 경우. 추정량은 매우 이상한 값을 보여줌
○ 도구변수의 강함 테스트
○ 1st stage F 통계량 계산하였을 때 F가 10보다 크면 그 도구변수는 강함
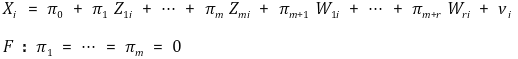
○ homoskedasticity에서만 사용 가능
○ W1i, ···, Wri는 도구변수의 강함과 무관
② instrument exogeneity
○ 수식화
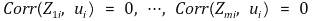
○ u를 특정해야 instrument exogeneity를 알 수 있음
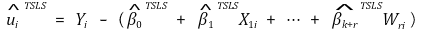
○ over-identifying restrictions test
○ 다음과 같은 통계량을 계산하였을 때 J는 자유도가 m-k인 카이제곱분포를 따름
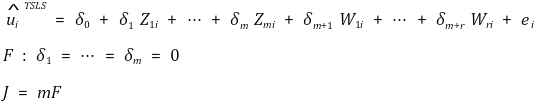
○ J에 대한 귀무가설 H0 : instrument variable들이 exogenous함
○ 논리는 instrument relevance와 비슷함 : F 통계량이 작으면 correlation이 없다(모든 계수가 0)는 의미
○ homoskedasticity에서만 사용 가능 : 많은 통계 프로그램은 heteroskedasticity-robust J-test도 제공
○ 귀무가설을 기각 시 어느 도구변수가 endogenous한 지 알 수 없음
○ J 통계량의 자유도의 의미
○ k개의 도구변수는 잔차를 만드는 데 쓰임 : k개의 endogenous variable과 대응됨
○ 나머지 m-k개의 도구변수는 잔차와의 상관관계를 테스트하는 데 사용됨
○ exactly identified인 경우 상관관계를 분석할 도구변수가 없으므로 J 테스트 적용 불가 : J 통계량은 이 경우 항상 0이 나옴
③ no perfect collinearity
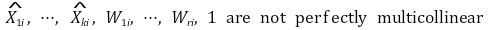
⑷ 행렬표현
① 모델링

○ Xi와 Zi가 겹칠 수 있음
② 가정
○ Yi = Xitβ + ui
○ (Yi, Xi, Zi), i = 1, ···, N is i.i.d
○ E(ui | Zi) = 0
○ E(ZiXit), E(ZiZit)는 역행렬이 존재
○ Zi, Xi, ui는 유한한 4차 적률이 있음
③ 과정
○ 1st. Xi를 도구변수 Zi로 회귀
○ 2nd. Xi의 추정량을 계산
○ 3rd. Yi를 Xi의 추정량으로 회귀
④ 추정량
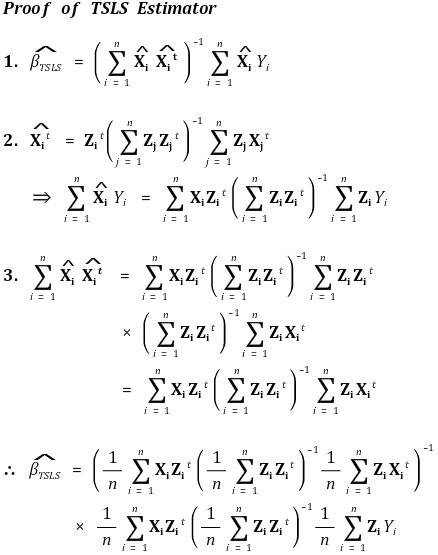
⑤ 일관성(consistency)
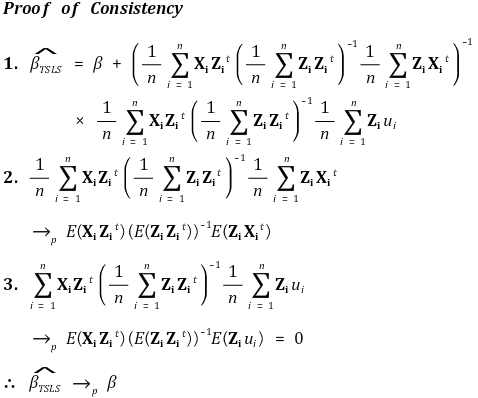
⑥ 정규근사성(asymptotic normality)
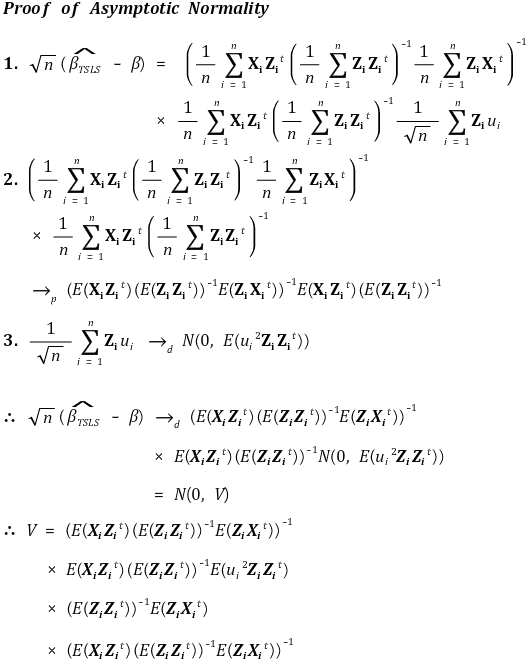
⑦ 정규분포 분산의 추정량
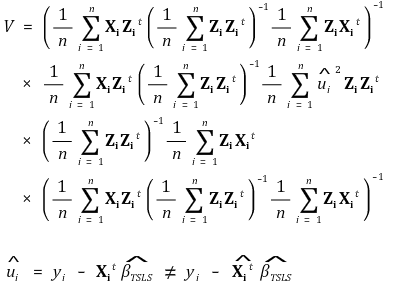
⑸ 도구변수 탐색 : 도구변수 탐색은 예술의 영역임
① Joshua Angrist (MIT)
② Steven Levitt (Chicago) : "Freakonomics"를 집필
③ Daron Acemoglu (MIT) : "Why Nations Fail"을 집필
4. 랜덤 통제 실험(randomized controlled experiment) [목차]
⑴ 개요
① 정의 : 모집단에서 피실험자들을 랜덤추출한 뒤 다시 랜덤하게 그룹을 나누어 처리(treatment)를 달리 하는 것
② 계량경제학에서 랜덤 통제 실험은 드묾
③ 랜덤 통제 실험을 하면 omitted variable bias를 제거할 수 있음 : 타당도가 100% 보장되지 않음
④ 어느 것을 인과관계로 판단할지에 대한 기준을 제시
⑵ 수식화
① 단순 모델
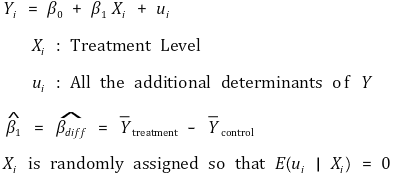
② 추가적인 회귀변수를 포함하는 모델

③ 추가적인 회귀변수를 추가하는 이유
○ 이유 1. 랜덤 체크(randomization check)
○ 추가적인 회귀변수의 유무에 관계없이 β1은 consistent함
○ 추가적인 회귀변수의 유무에 따라 β1이 크게 바뀌면 랜덤하지 않았던 것임
○ 이유 2. 효율성 : 추가적인 회귀변수가 있으면 더 분산이 작음
○ 이유 3. 조건부 랜덤화
○ 사람 개개의 특성에 따라 랜덤하게 추출한 것 같아도 랜덤하지 않을 수 있음
○ 추가적인 회귀변수가 고정된 상태에서 랜덤추출을 하면 그러한 우려를 최소화할 수 있음
○ β1 추정량이 consistent하려면 다음과 같은 조건부 독립을 만족해야 함 : 독립보다 요구조건이 약함
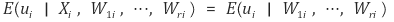
○ 상호작용 : treatment effect는 W에 의존할 수 있음
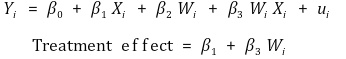
⑶ 내부적 타당도 위협(threats to internal validity)
① 랜덤처리 실패(failure to randomize)
○ treatment effect뿐만 아니라 nonrandom assignment effect가 나타남
○ 가설 검정 : pre-treatment characteristic인 W1i, ···, Wri로 Xi를 회귀했을 때 각 계수들이 모두 0이면 랜덤처리
○ 예 : 만일 이름으로 랜덤처리를 하는 경우 특정 민족이 처리군으로 많이 배정될 수 있음
② 처리 프로토콜 적용 실패(failure to follow treatment protocol, partial compliance)
○ 정의 : 랜덤처리가 잘 이루어져도 피실험자가 제대로 안할 수 있음
○ 이로 인해 Xi와 ui가 상관관계를 가질 수 있음
○ randomized encourage design : 랜덤처리를 도구변수로 하고, 실제 처리를 도구변수 회귀하면 적용 실패 여부를 알 수 있음
③ attrition
○ 정의 : 랜덤추출 후 treatment와 관련 있는 이유로 피실험자가 제외되는 것
④ 호손효과(Hawthorne effect)
○ 정의 : 피실험자가 자신이 어떤 실험을 수행하는지를 아는 것 자체가 실험 결과에 영향을 줄 수 있음
○ 신약 연구에서는 이중맹검을 통해 피해갈 수 있음
○ 계량경제학에서는 이중맹검을 하기 어려움
⑤ 작은 샘플(small sample)
○ 사람과 관련된 연구는 비싸기 때문에 샘플 사이즈가 작음
○ 많은 통계적 추정이 정규근사성을 기반으로 함
○ 샘플 사이즈가 작으면 정규분포로 추정하면 안 됨
⑷ 외부적 타당도 위협(threats to external validity)
① 대표성이 없는 샘플(non-representative sample)
○ 일반적인 계량경제 실험은 학부생 자원봉사자를 대상으로 함
○ 자원봉사자들은 더 동기부여가 돼 있어 효과가 과대평가될 수 있음
② 대표성이 없는 프로그램 또는 정책(non-representative program or policy)
○ 실험 프로그램 또는 정책이 실제와 유사해야 함
○ 예 : 실험 프로그램은 짧은 시간 동안 수행됨. 실제 궁금한 영역은 더 긴 시간이 요구될 수 있음
③ general equilibrium effect
○ 정의 : treatment로 인해 전체 환경이 바뀌고 이로 인해 treatment의 효과가 증폭되거나 억제될 수 있음
○ 작은 실험에서는 그 환경의 변화가 반영되지 않아 외부적 타당도를 별도로 고려해야 함
5. 유사실험(quasi-experiment) [목차]
⑴ 정의
① 독립변인이 실험자의 통제 하에 있지 않고 자연적인 상황에서 이루어지는 실험
② 자연실험(natural experiment)이라고도 함
③ 유사실험 목적 : 프로그램 평가(program evaluation)
⑵ 방법 1. DID 추정량(differences-in-differences estimator)
① 가장 단순한 모형 (패널 데이터 기준)

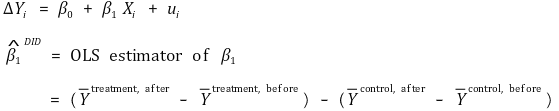
② 추가 회귀변수가 있을 때 모형 (패널 데이터 기준) : 전후 데이터 사이에 다른 조건이 바뀔 수도 있으므로
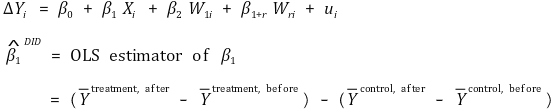
③ repeated cross-sectional data 기준
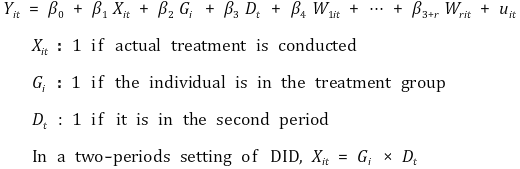
⑶ 방법 2. 도구변수 회귀
① 1st. Zi를 랜덤 통제 실험을 했을 때의 회귀변수로 정의
② 2nd. Zi는 Xi에 대한 좋은 도구변수 : instrument relevance 만족
③ 3rd. Yi는 관심이 있는 결과값
④ 4th. Zi를 도구변수로 하여 Yi에 대한 Xi의 효과를 평가
⑷ 방법 3. 회귀단절모형(RDD, regression discontinuity design)
① 개요
○ 역치(컷오프, threshold, cut-off) ω0를 설정하면 역치 근처의 데이터는 비슷하다고 할 수 있음
○ 역치 근처의 데이터에 처리를 달리하면 그 차이는 온전히 treatment effect라고 볼 수 있음
○ 매우 인기 있는 실험 기법
○ 단점 : outlier에 대해서 회귀 단절 모형을 적용하기 어려움
② sharp regression discontinuity design

Figure. 4. sharp regression discontinuity design
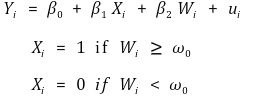
③ fuzzy regression discontinuity design
○ sharp regression discontinuity design에서 정의한 Xi처럼 매끄럽게 실험이 안될 수도 있음
○ 다음과 같은 도구변수 Zi는 실제 Xi에 대한 좋은 도구변수가 될 수 있음
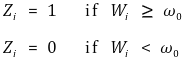
⑸ 내부적 타당도 위협(threats to internal validity)
① 랜덤처리 실패(failure to randomize)
○ treatment effect뿐만 아니라 nonrandom assignment effect가 나타남
○ 가설 검정 : pre-treatment characteristic인 W1i, ···, Wri로 Xi를 회귀했을 때 각 계수들이 모두 0이면 랜덤처리
○ 예 : 만일 이름으로 랜덤처리를 하는 경우 특정 민족이 처리군으로 많이 배정될 수 있음
② 처리 프로토콜 적용 실패(failure to follow treatment protocol, partial compliance)
○ 정의 : 랜덤처리가 잘 이루어져도 피실험자가 제대로 안할 수 있음
○ 이로 인해 Xi와 ui가 상관관계를 가질 수 있음
○ randomized encourage design : 랜덤처리를 도구변수로 하고, 실제 처리를 도구변수 회귀하면 적용 실패 여부를 알 수 있음
③ attrition
○ 정의 : 랜덤추출 후 treatment와 관련 있는 이유로 피실험자가 제외되는 것
④ 호손효과 없음
○ 유사실험에서 호손효과를 주의할 이유가 전혀 없음 : 자연실험이므로
⑤ 도구변수 유효성
○ instrument relevance는 데이터를 통해 평가할 수 있음
○ 도구변수가 랜덤하게 할당된 것으로 보여도 instrument exogeneity가 갖춰지지 않을 수 있음
○ 예 : 징병 추첨제(draft lottery)의 숫자에 따른 소득을 보고자 하는 경우에도 낮은 숫자가 뽑힌 사람들이 징집을 피하기 위한 행동을 유도하면서 Xi와 ui가 상관관계를 가질 수 있음
⑹ 외부적 타당도 위협(threats to external validity)
① 대표성이 없는 샘플(non-representative sample)
② 대표성이 없는 프로그램 또는 정책(non-representative program or policy)
③ general equilibrium effect
⑺ 비판
① quasi-experiment에서는 좋은 변수들을 찾기 위한 시도가 이루어짐
② 정말 좋은 quasi-experiment는 그렇게 많지 않음
6. heterogeneous population [목차]
⑴ 정의 : 회귀선의 계수 β0i, β1i가 상수가 아니고 표본에 따라 바뀌는 경우
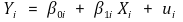
① β1i : Xi의 heterogeneous effect
② 관심있는 파라미터는 E(β1i)임
③ β1i가 관측 가능한 경우 상호작용(interaction)을 이용한 모델이 이용될 수 있음
④ β1i가 관측 불가능한 경우 아래와 같이 분석됨
⑵ OLS
① 가정 : Xi가 랜덤할 것 → Xi와 (ui, β0i, β1i)가 독립일 것
○ 실제로 만족하기 어려운 조건
② 수식화
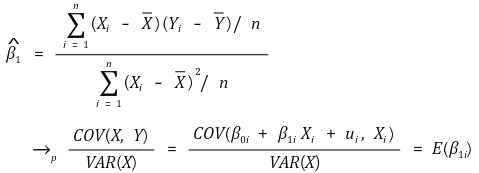
⑶ IV(instrumental variables estimation)
① 가정 : Zi가 랜덤할 것 → Zi와 (ui, vi, β0i, β1i, π0i, π1i)가 독립일 것
② 수식화
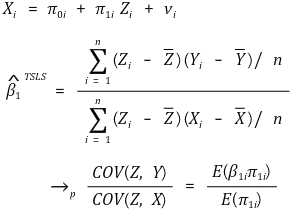
○ E(β1iπ1i) / E(π1i)를 LATE(local average treatment effect)라고 함
③ LATE와 ATE가 같아지기 위한 조건
○ 경우 1. β1i = β1 = 상수 : 이분산성이 없을 것
○ 경우 2. π1i = π1 : 도구변수에 이분산성이 없을 것
○ 경우 3. β1i와 π1i가 독립일 것
④ 함축
○ instrument exogeneity는 평가하기 어려움
○ J-test는 LATE들의 차이만을 알려줌
입력: 2019.11.26 10:29
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 20강. 회귀분석의 분산분석 (0) | 2019.12.07 |
|---|---|
| 【통계학】 통계학 요점 정리 (0) | 2019.12.07 |
| 【통계학】 16강. 선형 회귀분석 (0) | 2019.11.24 |
| 【통계학】 1-1강. 분위수 대 분위수 플롯(Q-Q plot) (0) | 2019.10.10 |
| 【통계학】 14-7강. 카이제곱검정 테스트 (3종류) (0) | 2019.10.05 |




최근댓글