16강. 선형 회귀분석(linear regression analysis)
추천글 : 【통계학】 통계학 목차
a. R로 하는 회귀분석
1. 회귀분석 [목차]
⑴ 회귀분석(regression analysis) : 특정 변수를 하나 또는 복수의 다른 변수의 의존관계로 나타내는 것
① 더 정확하게는, y ~ X (단, y ∈ ℝ)
○ supervised algorithm에 속함
○ (참고) classification : y ~ X (단, | { y } | < ∞ )
② 특정 변수 : 종속변수(dependent variable)라는 명칭이 대표적이나 여러 명칭이 있음
○ 응답변수(반응변수, response variable)
○ 결과변수(outcome variable)
○ 표적변수(target variable)
○ 출력변수(output variable)
○ 예측된 변수(predicted variable)
③ 다른 변수 : 독립변수(independent variable)라는 명칭이 대표적이나 여러 명칭이 있음
○ 실험변수
○ 설명변수(explanatory variable)
○ 예측변수(predictor variable)
○ 회귀자(regressor)
○ 공변량(covariate)
○ 통제변수(controlled variable)
○ 조작변수(manipulated variable)
○ 노출변수(exposure variable)
○ 리스크 팩터(risk factor)
○ 입력 변수(input variable)
○ 변수(feature)
⑵ (구별개념) 교차분석, 분산분석
① 회귀분석 : 독립변수는 측정형 변수임. 종속변수는 측정형 변수임
○ 회귀분석은 종속변수에 대한 독립변수의 인과관계를 나타낸 것임
○ 실제 인과관계를 입증하지 않아도 됨 (∵ 예측이 목적이기 때문)
○ 예 : 6세 아이의 uncalcified bone의 길이는 추가로 성장할 키를 예측하지만 인과관계가 있는 것은 아님
② 교차분석 : 독립변수는 범주형(분류형) 변수임. 종속변수는 범주형(분류형) 변수임
○ 교차분석은 단순히 변수들 간의 상관관계를 나타낸 것임
③ 분산분석 : 독립변수는 범주형(분류형) 변수임. 종속변수는 측정형 변수임
⑶ 단순회귀분석과 다중회귀분석
① 단순회귀분석(simple regression analysis) : 독립변수가 하나인 회귀분석
② 다중회귀분석(multiple regression analysis) : 독립변수가 둘 이상인 회귀분석
⑷ 변수 선택 방법
① 전진 선택법(forward selection)
○ 단계 1. 절편만 있는 상수 모형부터 시작
○ 단계 2. 중요하다고 생각되는 독립변수를 차례로 모형에 추가하는 방식
② 후진 소거법(backward elimination)
○ 단계 1. 독립변수 후보 모두를 포함한 모형에서 출발
○ 단계 2. 제곱합의 기준으로 가장 적은 영향을 주는 변수부터 하나씩 제거
○ 단계 3. 더 이상 유의하지 않은 변수가 없을 때까지 독립변수들을 제거
○ 단계 4. 이때의 모형을 선택
③ 단계적 방법(stepwise method)
○ 단계별 추가 : 변수를 추가하면서 새롭게 추가된 변수에 기인해 기존 변수가 그 중요도가 약화되면 해당 변수를 제거
○ 단계적 제거 : 제거되는 변수의 여부를 검토해 더 이상 없을 때 중단하는 방법
⑸ 모형 선택 기준
① 개요
○ 모형의 복잡도에 벌점(penalty)을 주는 방법
○ 모든 후보 모형들에 대해 AIC, BIC를 계산하고 그 값이 최소가 되는 모형을 선택
② AIC(Akaike information criterion)
○ AIC = -2 ln (L) + 2p (단, ln (L)은 모형의 적합도, L은 우도함수, p는 매개변수 개수)
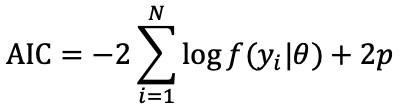
○ 취지 : 파라미터가 많으면 모형이 과적합되므로 파라미터의 개수만큼 panelize
○ 실제 데이터의 분포와 모형이 예측하는 분포 사이의 차이를 나타낸 지표
○ 값이 낮을수록 모형의 적합도가 높음
○ 표본이 커질수록 부정확해짐
③ BIC(Bayesian information criterion)
○ BIC = -2 ln (L) + p ln n (단, ln (L)은 모형의 적합도, L은 우도함수, p는 매개변수 개수, n은 데이터 개수)
○ 표본의 커질수록 부정확해지는 AIC를 보완
○ 표본의 크기가 커질수록 복잡한 모형을 더 강하게 처벌
④ AICc
○ AICc = AIC + 2K(K+1) / (N-K-1) (단, N은 표본의 개수)
○ 취지 : AIC가 표본이 커질수록 부정확해지는 문제를 해결하기 위함
2. 단순선형회귀모델(simple linear regression model) [목차]
⑴ 정의 : 단순회귀분석 중 의존관계가 일차함수로 나타나는 경우
⑵ 자료의 표현
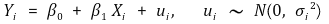
① β0 : y 절편(y intercept)
② β1 : 기울기(slope) 또는 X의 계수(coefficient on X)
○ parameter, regression coefficient, weight 등으로도 불림
○ 직관적으로 탄력성(elasticity)은 기울기의 절대값이 큰 정도를 의미
○ 미시경제학에서 탄력성(elasticity)은 기울기에 (-1)을 곱한 것을 의미
③ 회귀선의 종류
○ 실제회귀선(population regression line) : 모집단의 특성을 통해 얻은 회귀선
○ 적합회귀선(fitted regression line) : 표본의 특성을 통해 얻은 회귀선
④ ui : 잔차(residual)
⑤ 잔차와 오차(error)의 차이
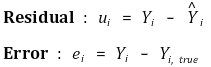
○ (참고) 앞으로 언급되는 오차는 사실상 잔차를 의미함
⑥ 분산성
○ 등분산성(homoscedasticity) : VAR(ui | Xi)가 Xi와 독립. 비현실적 가정. 많은 통계 프로그램의 디폴트 셋팅
○ 이분산성(heteroscedasticity) : VAR(ui | Xi)가 Xi에 의존
○ (참고) 등분산성이 있는 모델은 좋은 모델임
⑶ 가정
① 가정 1. Xi가 오차에 대한 어떤 정보도 제공하지 않음
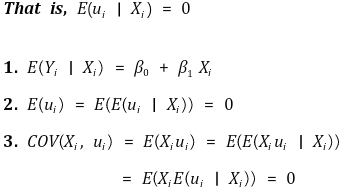
○ residual plot이 패턴이 있으면 좋은 모델이 아님
② 가정 2. (Xi, Yi)는 i.i.d.
③ 가정 3. 4차 적률(4th order moment)의 존재성
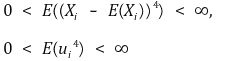
⑷ 적합회귀선의 유도
① 방법 1. 적률방법 또는 표본유사 추정
○ 계산과정
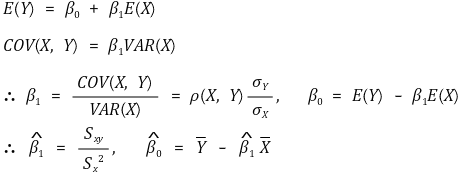
② 방법 2. 최소제곱법(method of least squares) 또는 OLS(ordinary least squares)
○ 정의 : SSE(sum of squares of the errors)의 최솟값을 계산
○ 모든 통계 소프트웨어에서 제공
○ 계산 과정 : Xi가 1차원인 경우
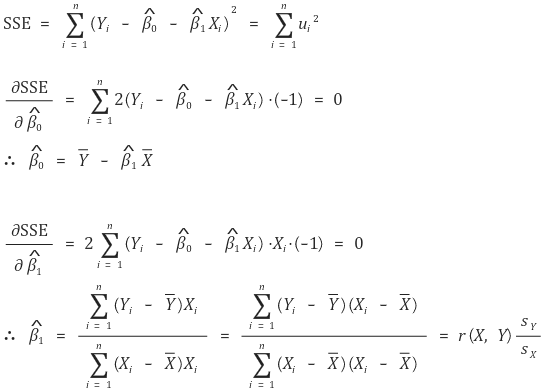
○ 최소제곱법은 최대우도 추정에 근거함 (단, 잔차가 등분산성, 정규성을 가질 것을 요함)

○ Y에 대한 X의 회귀와 X에 대한 Y의 회귀는 일반적으로 동일하지 않음
○ Y에 대한 X의 회귀곡선은 E(X2), E(XY), E(X) 등이 관여함
○ X에 대한 Y의 회귀곡선은 E(Y2), E(XY), E(Y) 등이 관여함
○ E(X2), E(Y2)이 비대칭성을 만듦
③ 방법 3. cross entropy
○ 일반적인 정의
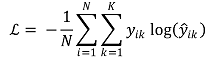
○ 이진 분류
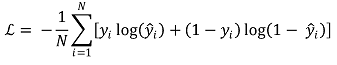
○ y가 one-hot vector [0, ···, 1, ···, 0]으로 표현된다면 다음과 같이 나타낼 수 있음

⑸ 회귀선의 특징
① 개요

② 불편성(unbiasedness)
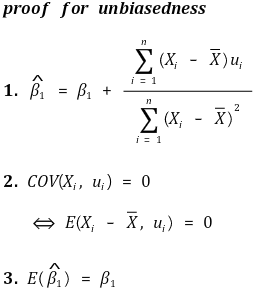
③ 효율성(efficiency)
○ Gauss-Markov theorem : OLS는 homoscedasticity 조건 하에서 efficient함
④ 일관성(consistency)

⑤ 정규근사성(asymptotic normality)
○ 기울기(slope)
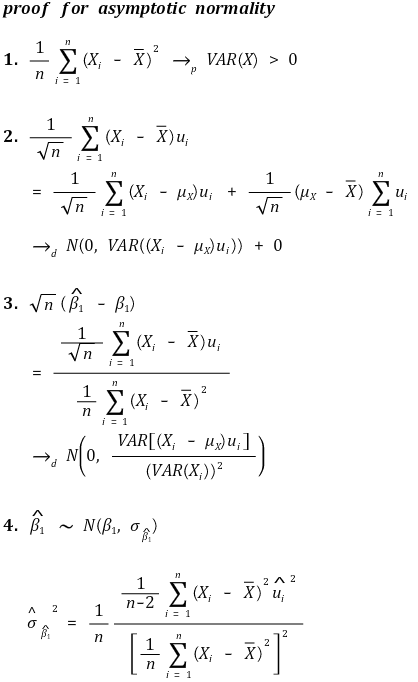
○ y절편(y intercept) - 이분산성 표준 에러(heteroscedasticity-robust standard error)
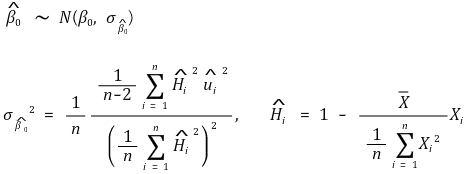
○ y절편(y intercept) - 등분산성 표준 에러
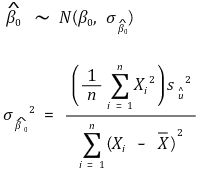
⑹ 회귀선의 평가
① 기준 1. linearity
② 기준 2. homoscedasticity : 잔차 항이 등분산성을 갖는 것
③ 기준 3. normality : 잔차 항이 정규분포를 따르는 것
○ Box-Cox : 선형회귀모형에서 정규성 가정이 성립한다고 보기 어려울 경우 종속변수를 정규분포에 가깝게 변환
⑺ 결정계수(coefficient of determination, R-squared)
① 결정계수 R2
○ 정의
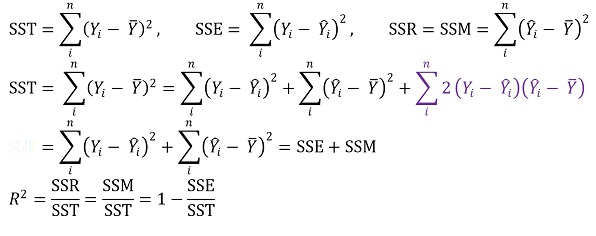
○ SST : 총 변동
○ SSR : 회귀식에 대한 변동
○ SSE : 에러에 의한 변동
○ SSE는 RSS(residual sum of squares), SSR(sum of squared residuals)라고도 함
○ ■ 항이 0인 이유 : bias와 chance error의 공분산은 직관적으로 0이기 때문
○ 의미
○ 의미 1. Y의 분산 중 X가 설명할 수 있는 부분의 비율. 단위 없음
○ 의미 2. 회귀직선에 의해 설명되는 제곱합 ÷ 총 제곱합
② 결정계수는 상관계수의 제곱과 동일
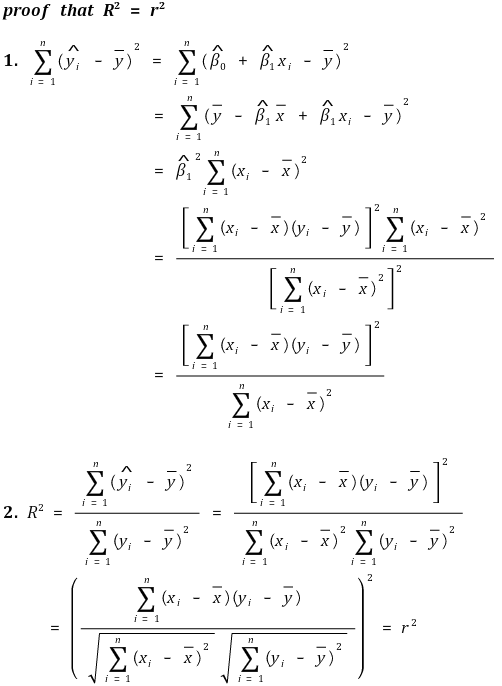
③ FVR(fraction of the variance unexplained)
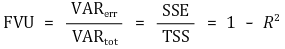
④ 성질
○ 0 ≤ R2 ≤ 1
○ R2이 1에 가까울수록 적합회귀선의 적합성(goodness of fit of regression line)이 좋음
○ β1의 추정량 = 0 ⇒ R2 = 0
○ R2 = 0 ⇒ β1의 추정량 = 0 또는 Xi = 상수
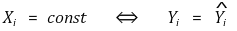
⑻ 평균오차회귀
① SSE의 전개
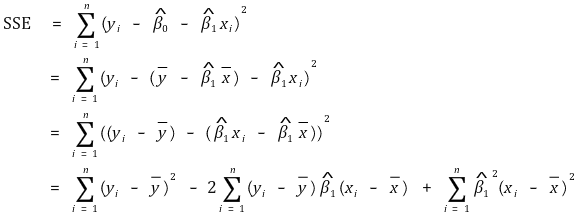
② SSE의 기댓값
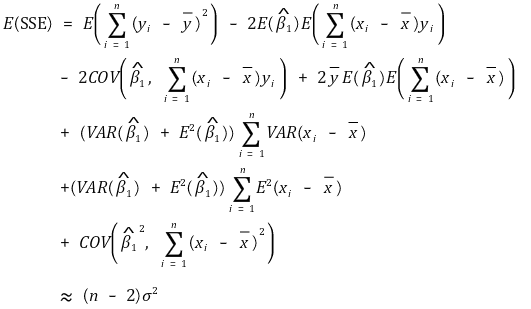
○ 전체 자유도 = 잔차의 자유도 + 회귀선의 자유도
○ 전체 자유도는 n-1
○ 회귀선의 자유도는 1 (∵ 회귀변수가 하나이기 때문)
○ 잔차의 자유도는 n-2
③ 평균제곱오차(MSE, mean squared error)
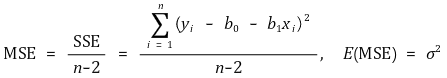
④ 표준오차회귀(SER, standard error regression)
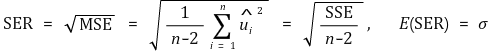
⑤ SSE와 모분산의 불편추정량
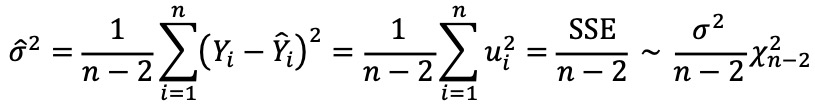
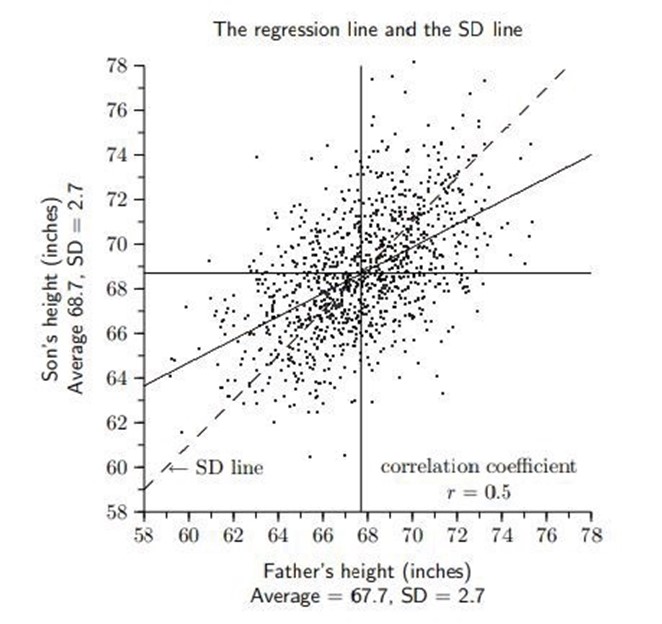
⑼ 예제 1. 회귀의 어원
① X : 아버지의 키
② Y : 아들의 키
③ E(X) = 67.7, E(Y) = 68.7, σX = 2.7, σY = 2.7, ρXY = 0.5
④ E(Y | X = 80) = 74.85
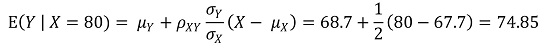
⑤ E(Y | X = 60) = 64.85
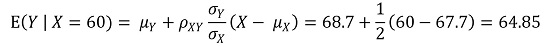
⑥ 결론
○ 키가 큰 아버지의 아들은 키가 작아지는 경향이 있음
○ 키가 작은 아버지의 아들은 키가 커지는 경향이 있음
○ 최종적으로 아들의 키는 평균으로 회귀하는 경향이 있음
○ 다만, 위 경향성은 기댓값에 불과하므로 아들의 키와 아버지의 키의 분산 대소관계는 전혀 별개임
⑽ 예제 2. 독립변수 범위 외에서 Y값 예측 : extrapolation이라고도 함
① 일반적으로 extrapolation은 위험함
② extrapolation 방법론이 항상 틀린 것은 아님
○ 예 : 생물 진화론 연구
⑾ 예제 3. 선형회귀분석과 이변량 정규분포
⑿ 파이썬 코드
from sklearn import linear_model
reg = linear_model.LinearRegression()
reg.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
# LinearRegression()
reg.coef_
# array([0.5, 0.5])
3. 다중선형회귀모델(multiple linear regression model) [목차]
⑴ 정의 : 다중회귀분석 중 의존관계가 일차함수로 나타나는 경우
⑵ omitted variable bias
① 정의 : omitted variable로 인해 오차의 기댓값이 0이 아닌 현상
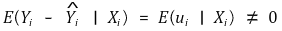
○ endogenous variable : ui와 상관관계가 있는 변수들
○ exogenous variable : ui와 상관관계가 없는 변수들
② 조건 1. omitted variable과 regressor(e.g., Xi)가 상관관계를 가지고 있을 것
③ 조건 2. omitted variable이 Y의 determinator일 것
④ 기울기의 수렴값
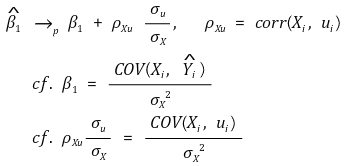
○ ρXu > 0 : upward bias
○ ρXu < 0 : downward bias
⑤ 새로운 변수를 추가했을 때 계수의 값이 크게 바뀌면 omitted variable bias가 있었다고 할 수 있음
⑶ 자료의 표현
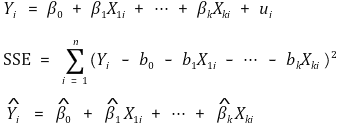
① 위 추정량들은 unbiasedness, consistency, asymptotically jointly normal이 관찰
② 강건성(robustness) : 새로운 regressor를 추가해도 어떤 regressor의 slope 값도 크게 바뀌지 않는 것
③ 민감도(sensitivity) : 새로운 regressor를 추가하면 특정 regressor의 slope 값이 크게 바뀌는 것
⑷ 가정
① 가정 1. 오차는 X1i, ··· Xki로 설명되지 않음
② 가정 2. (X1i, ··· Xki,Yi)는 i.i.d.
③ 가정 3. 4차 적률(4th order moment)의 존재성
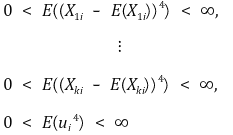
④ 가정 4. 완전 다중공선성(perfect multicollinearity)이 없을 것
○ 다중공선성 : 한 독립변수와 다른 독립변수들의 선형결합이 상당히 상관관계가 있는 것
○ (참고) 다중선형회귀모델은 독립변수끼리 독립적이기를 기대함
○ 완전 다중공선성 : 한 regressor가 다른 regressor들의 완전 선형성이 있는 경우 (행렬식 = 0)
○ 완전 다중공선성은 변수의 성질이 아니라 데이터 세트의 성질
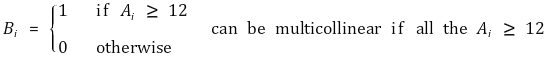
○ 완전 다중공선성 데이터에 회귀분석을 시도하면 가능한 계수들의 경우의 수는 무한 : 회귀분석 불가능
○ 불완전 다중공선성(imperfect multicollinearity) : 2 이상의 regressor가 상당히 높은 상관관계를 보이는 것
○ 일단 문제가 되지는 않음
○ 기울기 추정량의 분산이 상당히 큼 → 기울기의 추정량을 신뢰하기 어려움
Figure. 4. 다중공선성이 기울기 추정량의 분산을 증가시키는 이유
⒝ 상당히 다양한 평면이 오차범위 안에 존재할 수 있음
○ 일반적으로 한 쌍의 변수의 상관계수가 0.9 이상이면 안 됨
○ 해결방법
○ 모든 조합의 pairwise plot을 그린 뒤 상관관계가 큰 변수를 제거
○ PCA, weighted sum 등의 방법을 시도하기도 하지만 각각 단점이 존재
○ (참고) R STUDIO에서 완전 다중공선성 데이터를 회귀분석하는 경우 문제가 되는 항 중 가장 마지막 항을 임의로 무시
⑸ OLS 추정량 : 아래와 같은 연립방정식을 계산하여 계수를 결정
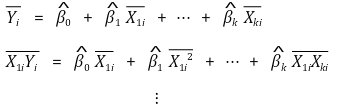
⑹ 회귀선의 특징
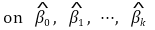
① unbiasedness
② consistency
③ asymptotically jointly normality
④ Frisch-Waugh theorem

⑺ 수정된 결정계수 (adjusted R2)
① R2의 단점 : 다중회귀모델에서 fitting 정도를 잘 반영하지 못함
○ 단점 1. R2는 regressor의 개수가 증가할 때마다 항상 증가 (∵ SSE의 최솟값이 감소하므로)
○ 단점 2. R2이 높다고 omitted variable bias가 없는 게 아님
○ 단점 3. R2이 높다고 적절한 regressor을 찾은 게 아님
○ 단점 1을 해결하기 위해 adjusted R2을 도입
② 수식화
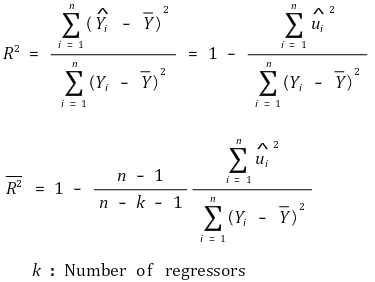
③ 성질
○ adjusted R2 ≤ R2
○ adjusted R2는 음수가 될 수도 있음
○ 적절하지 않은 변수들을 추가할수록 그 값이 감소함
⑻ 표준오차회귀(SER, standard error regression) : k는 회귀식의 독립변수의 수
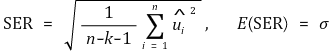
⑼ 결합 가설(joint hypothesis) : 둘 이상의 제한조건이 있을 때의 가설
① 발상 1. t1과 t2가 독립
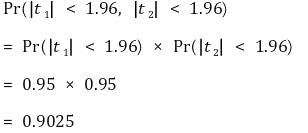
② 발상 2. t1과 t2가 다중공선성
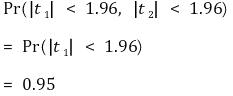
③ 일반적인 경우

○ 일반적으로 이분산성(heteroscedastic-robust) F-통계량을 사용
○ 많은 통계 프로그램이 등분산성 F-통계량을 디폴트로 설정
④ 귀무가설
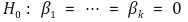
⑽ 다중선형회귀모델 재정의
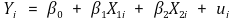
① H0 : β1 = β2를 검정하고 싶은 경우
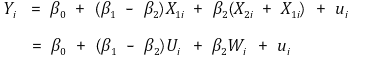
② H0 : β1 + β2 = 1을 검정하고 싶은 경우
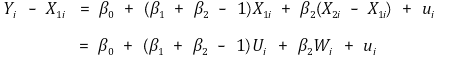
⑾ 조건부 기댓값 독립(conditional mean independence)
① 정의
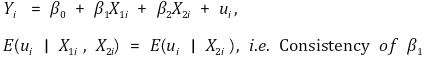
② X1i는 주어진 X2i에 대해 ui와 상관관계 없음
③ β2는 consistency가 없을 수 있음 : 그러나 중요하지 않음
⑿ 행렬표현(matrix notation)
① 선형회귀모델
○ 스칼라 Y, 열벡터 X, β에 대해,
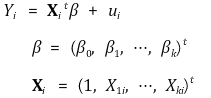
○ 일반화
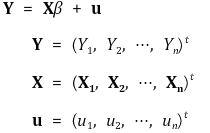
② 가정
○ 가정 1. E(ui | Xi) = 0
○ 가정 2. (Xi, Yi), i = 1, ···, n이 i.i.d.
○ 가정 3. Xi와 ui는 nonzero finite fourth moment를 가지고 있음
○ 가정 4. 0 < E(XiXit) < ∞, 완전 다중공선성이 없을 것
③ OLS 모델링 - 단순한 버전
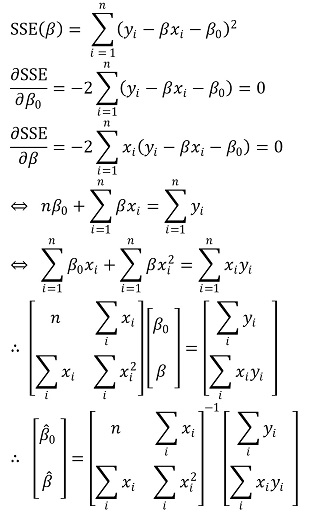
④ OLS 모델링
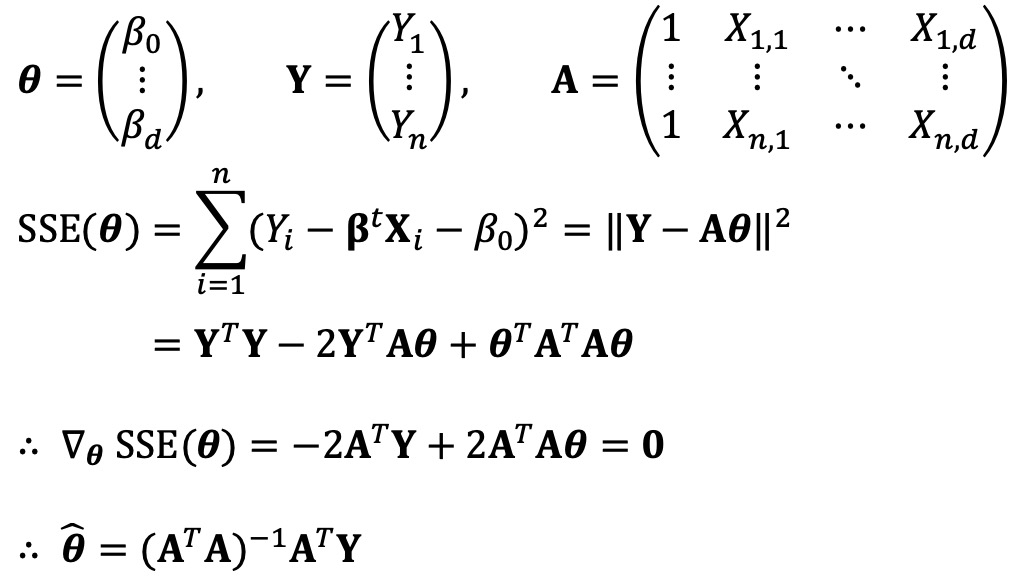
⑤ consistency
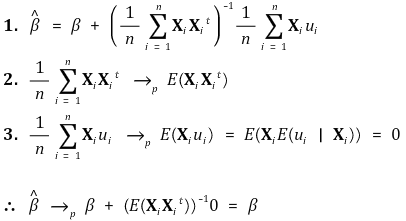
⑥ multivariate central limit theorem
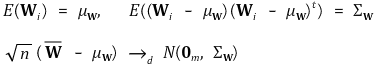
⑦ asymptotic normality
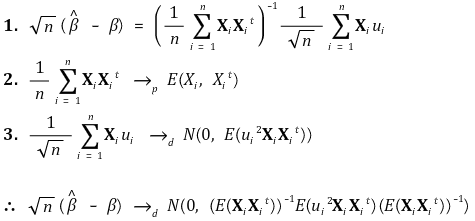
⑧ robust standard error (Eicker-Huber-White standard error)
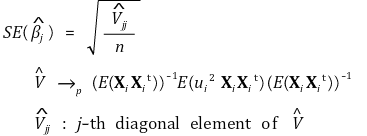
⑨ robust F
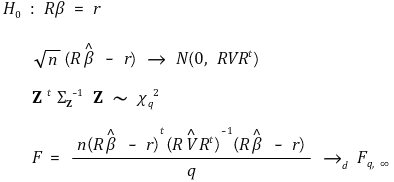
입력: 2019.06.20 23:26
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 통계학 요점 정리 (0) | 2019.12.07 |
|---|---|
| 【통계학】 19강. 고급 회귀분석 (0) | 2019.11.26 |
| 【통계학】 1-1강. 분위수 대 분위수 플롯(Q-Q plot) (0) | 2019.10.10 |
| 【통계학】 14-3강. 카이제곱검정 테스트 (3종류) (0) | 2019.10.05 |
| 【통계학】 14-6강. Fisher Exact Test (hypergeometric test) (0) | 2019.08.24 |







최근댓글