14-3강. 카이제곱검정 테스트 (3종류)
추천글 : 【통계학】 14강. 통계적 검정
1. 카이제곱 단순적합도 검정 [본문]
2. 카이제곱 독립성 검정 [본문]
3. 카이제곱 동질성 검정 [본문]
4. 카이제곱분포와 중심극한정리 [본문]
1. 카이제곱 단순적합도 검정(chi-square goodness-of-fit test) [목차]
⑴ 문제상황(contingency table) : 유전 실험이라면 Oi와 Ej는 비율이 아니라 개체수를 의미함
Figure. 2. 카이제곱 단순적합도 검정 문제상황
⑵ 가설 설정
H0 : 표본 Xi들의 분포가 주어진 확률분포를 따름
H1 : 표본 Xi들의 분포가 주어진 확률분포를 따르지 않음
⑶ 검정통계량 계산
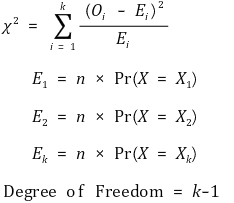
⑷ 기각역 : 유의수준 α. 샘플이 커야 잘 성립함
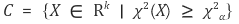
⑸ 다중 변수에 대한 카이제곱 단순적합도 검정도 가능함
| 1 | 2 | ⋯ | S | Total | |
| X(1) | N1(1) | N2(1) | ⋯ | NS(1) | n(1) |
| X(2) | N1(2) | N2(2) | ⋯ | NS(2) | n(2) |
| ⋮ | ⋮ | ⋮ | ⋱ | ⋮ | ⋮ |
| X(K) | N1(K) | N2(K) | ⋯ | NS(K) | n(K) |
| m1 | m2 | ⋯ | mS | n |
Table. 1. 다중 변수에 대한 카이제곱 단순적합도 검정

2. 카이제곱 독립성 검정(chi-square test of independence) [목차]
⑴ 문제상황(contingency table)
Figure. 3. 카이제곱 독립성 검정 문제상황
⑵ 가설 설정
H0 : X와 Y는 독립(independent)
H1 : X와 Y는 독립이 아님(not independent)
⑶ 검정통계량 계산 : 주변부 확률분포와 독립의 관계를 이용하여 예측값 생성

⑷ 기각역 : 유의수준 α. 샘플이 커야 잘 성립함
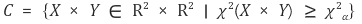
3. 카이제곱 동질성 검정(chi-square test of homogeneity) [목차]
⑴ 문제상황(contingency table)
Figure. 4. 카이제곱 동질성 검정 문제상황
⑵ 가설 설정
H0 : Group1과 Group2는 동일한 확률분포를 따름
H1 : Group1과 Group2는 동일한 확률분포를 따르지 않음
⑶ 검정통계량 계산
① 동일 확률분포는 독립과 분명히 개념이 다름
② 하지만 카이제곱 독립성 검정과 굉장히 유사한 계산을 거침

⑷ 기각역 : 유의수준 α. 샘플이 커야 잘 성립함
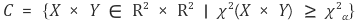
4. 카이제곱분포와 중심극한정리 [목차]
⑴ (참고) 중심극한정리(central limit theorem)

⑵ 카이제곱분포의 유도 : 이항분포를 따르는 Xi의 분산이 Var(Xi) = npq = np - np2 ≈ np = 𝔼[Xi]임을 이용하면,
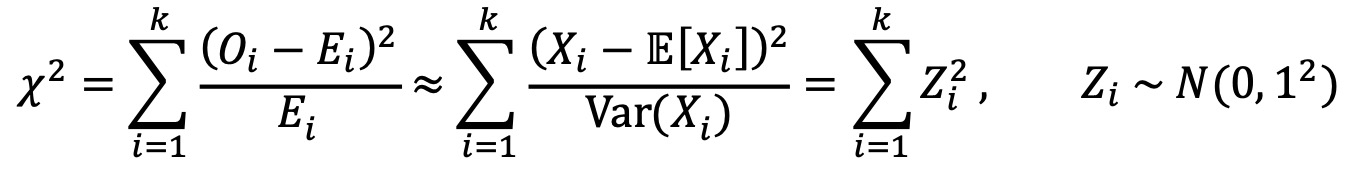
입력: 2019.10.05 11:13
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 16강. 선형 회귀분석 (0) | 2019.11.24 |
|---|---|
| 【통계학】 1-1강. 분위수 대 분위수 플롯(Q-Q plot) (0) | 2019.10.10 |
| 【통계학】 14-6강. Fisher Exact Test (hypergeometric test) (0) | 2019.08.24 |
| 【통계학】 14-9강. Kruskal-Wallis H test (0) | 2019.08.24 |
| 【통계학】 14-1강. 통계적 검정 예시 총정리 (0) | 2019.07.24 |








최근댓글