14-1강. 통계적 검정 예시 총정리
추천글 : 【통계학】 14강. 통계적 검정
1. 참고 [본문]
2. Xi ~ N(μ, σ2), σ2 is known [본문]
3. Xi ~ N(μ, σ2), σ2 is unknown [본문]
4. Xi ~ N(μ, σ2), μ is known [본문]
5. Xi ~ N(μ, σ2), μ is unknown [본문]
6. Xi ~ N(μx, σx2) (i = 1, ···, n), Yj ~ N(μy, σy2) (j = 1, ···, m), σx2, σy2 is known [본문]
7. Xi ~ N(μx, σ2) (i = 1, ···, n), Yj ~ N(μy, σ2) (j = 1, ···, m), σ2 is unknown [본문]
1. 참고 [목차]
⑴ X ~ N(0, 1)일 때 : P( x ∈ [zα, ∞) ) = α
⑵ X ~ χ2(n)일 때 : P( x ∈ [χ2(n)α, ∞) ) = α
⑶ X ~ T(n)일 때 : P( x ∈ [t(n)α, ∞) ) = α
2. Xi ~ N(μ, σ2), σ2 is known [목차]
⑴ H0 : μ = μ0, H1 : μ ≠ μ0 (유의수준 : α)

⑵ H0 : μ = μ0, H1 : μ > μ0 (유의수준 : α)
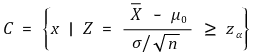
⑶ H0 : μ = μ0, H1 : μ < μ0 (유의수준 : α)

3. Xi ~ N(μ, σ2), σ2 is unknown [목차]
⑴ H0 : μ = μ0, H1 : μ ≠ μ0 (유의수준 : α)
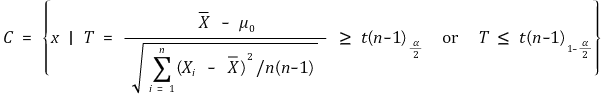
⑵ H0 : μ = μ0, H1 : μ > μ0 (유의수준 : α)
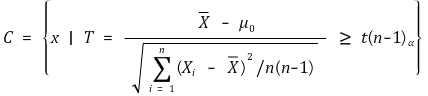
⑶ H0 : μ = μ0, H1 : μ < μ0 (유의수준 : α)
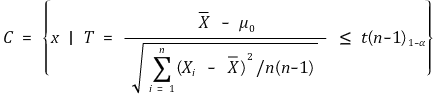
4. Xi ~ N(μ, σ2), μ is known [목차]
⑴ H0 : σ2 = σ02, H1 : σ2 ≠ σ02 (유의수준 : α)
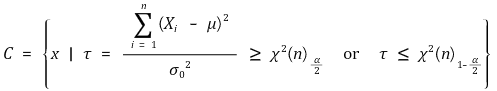
⑵ H0 : σ2 = σ02, H1 : σ2 > σ02 (유의수준 : α)
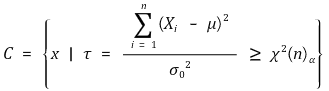
⑶ H0 : σ2 = σ02, H1 : σ2 < σ02 (유의수준 : α)
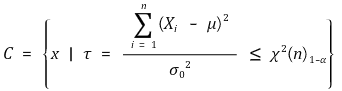
5. Xi ~ N(μ, σ2), μ is unknown [목차]
⑴ H0 : σ2 = σ02, H1 : σ2 ≠ σ02 (유의수준 : α)
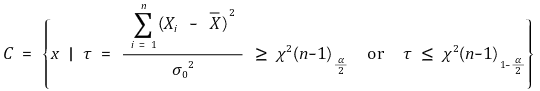
⑵ H0 : σ2 = σ02, H1 : σ2 > σ02 (유의수준 : α)
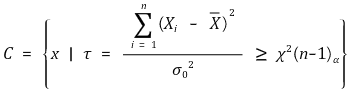
⑶ H0 : σ2 = σ02, H1 : σ2 < σ02 (유의수준 : α)
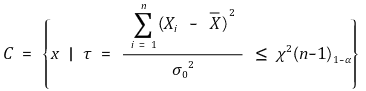
6. Xi ~ N(μx, σx2) (i = 1, ···, n), Yj ~ N(μy, σy2) (j = 1, ···, m), σx2, σy2 is known [목차]
⑴ H0 : μx = μy = μ, H1 : μx ≠ μy (유의수준 : α)
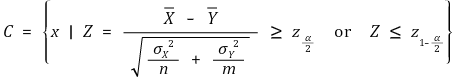
⑵ H0 : μx = μy = μ, H1 : μx > μy (유의수준 : α)
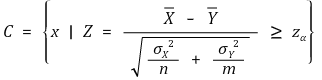
⑶ H0 : μx = μy = μ, H1 : μx < μy (유의수준 : α)
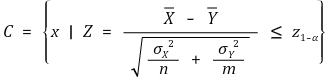
7. Xi ~ N(μx, σ2) (i = 1, ···, n), Yj ~ N(μy, σ2) (j = 1, ···, m), σ2 is unknown [목차]
⑴ H0 : μx = μy = μ, H1 : μx ≠ μy (유의수준 : α)
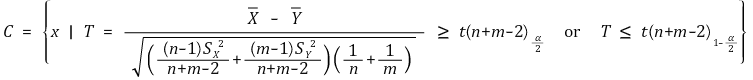
⑵ H0 : μx = μy = μ, H1 : μx > μy (유의수준 : α)
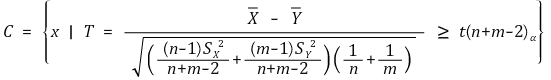
⑶ H0 : μx = μy = μ, H1 : μx < μy (유의수준 : α)
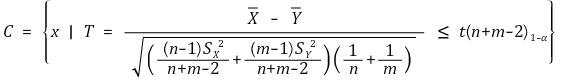
입력: 2019.07.24 20:59
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 14-6강. Fisher Exact Test (hypergeometric test) (0) | 2019.08.24 |
|---|---|
| 【통계학】 14-9강. Kruskal-Wallis H test (0) | 2019.08.24 |
| 【통계학】 3-2강. 몬티홀 문제 (0) | 2019.07.03 |
| 【통계학】 3-1강. 포함배제의 원리 (0) | 2019.06.27 |
| 【통계학】 15강. 분산분석(ANOVA) (5) | 2019.06.21 |




최근댓글