15강. 분산분석(ANOVA)
추천글 : 【통계학】 통계학 목차
a. R로 하는 분산분석
1. 분산분석(ANOVA, analysis of variance) [목차]
⑴ 정의 : n개의 집단을 비교하는 통계적 분석 (단, n > 2)
⑵ 제1종 오류의 누적(type Ⅰ error inflation) : n개의 집단에서 t 검정을 하는 경우 문제가 발생 (단, n > 2)
① 1개의 집단에서 제1종 오류가 발생하지 않을 확률 (유의수준 5%) : 0.95
② n개의 집단 모두 제1종 오류가 발생하지 않을 확률 (유의수준 5%) : 0.95n
③ 한 번이라도 제1종 오류가 발생할 확률(유의수준 5%) : 1 - 0.95n ≫ 0.05
④ 제1종 오류의 누적으로 인해 ANOVA가 대두됨
⑶ 가정 : one-way ANOVA, two-way ANOVA 모두에서 필요한 3대 가정
① 정규성(normality)
○ 정의 : 모든 데이터는 정규분포를 따르는 모집단들로부터 추출됨
○ 정규성 검정의 종류 : Q-Q plot, 샤피로-윌크 검정(Shapiro-Wilk), 콜모고로프-스미르노프 검정(Kolmogorov-Smirnov)
○ 정규분포라고 보기 곤란한 경우 멱 변환, 로그 변환을 사용하여 유사 정규분포로 만듦
○ Welch ANOVA F-test는 ANOVA 중 등분산성을 가정하지 않음
○ (참고) 모집단들이라고 표현한 까닭은 모집단의 평균이 다를 수 있기 때문
Figure. 1. 로그 변환을 통해 유사 정규분포로 만드는 예
② 독립성(independency) : i.i.d.라고도 함
○ 정의 : 모든 데이터는 모집단들로부터 독립적으로 추출됨
○ 실험 디자인의 문제
○ (참고) 모집단들이라고 표현한 까닭은 모집단의 평균이 다를 수 있기 때문
③ 등분산성(homoscedasticity)
○ 정의 : 모든 데이터는 평균이 달라도 분산은 동일한 모집단들로부터 추출됨
○ 가장 큰 분산과 가장 작인 분산이 4 : 1을 넘지 않으면 분산분석을 사용해도 됨
○ 분산분석을 사용하기 곤란한 경우 제곱근 변환을 사용하여 분산의 차이를 최소화 함
○ (참고) 회귀분석의 등분산성은 각 Xi에 대해 Yi의 분산이 같다는 것을 의미 : 약간의 의미 차이가 있음
○ (참고) 등분산성을 만족하지 않는 경우 Welch ANOVA를 적용해야 함
⑷ 강건성(robustness)
① 정의 : 많은 샘플수, 카테고리 내 동일 반복수 등을 만족 시 이분산성, 비정규성에서도 통계적 결론이 달라지지 않는 것
② ANOVA의 강건성 : 등분산성, 정규성이 엄격히 지켜지지 않아도 ANOVA가 잘 적용되는 것
③ (참고) 회귀분석의 강건성 : 회귀변수가 추가돼거나 변경되도 특정 계수의 값이 크게 달라지지 않는 것
⑸ (구별개념) 회귀분석, 교차분석
① 분산분석 : 독립변수는 범주형(분류형) 변수임. 종속변수는 측정형 변수임
② 교차분석 : 독립변수는 범주형(분류형) 변수임. 종속변수는 범주형(분류형) 변수임
③ 회귀분석 : 독립변수는 측정형 변수임. 종속변수는 측정형 변수임
2. 일원배치 분산분석(one-way ANOVA) [목차]
⑴ 정의 : 분산분석 중 종속변인이 1개, 독립변인이 1개인 경우
① 독립변인을 처리 효과 또는 인자라고 함
② 적절한 종속변인의 예 :{키}, {몸무게}(O)
③ 적절하지 않은 종속변인의 예 :{키, 몸무게} (X)
⑵ 일원 분산분석 모델
① 모델 1. 고정효과 모델링(fixed effect modeling)
○ 정의 : 특정 대상들의 효과를 비교해 보는 것. 즉 factor의 level이 정해져 있는 것
○ 방법 : 모집단에서 추출하는 행위를 요하지 않음. 사후검정 중요
○ 예 : 대조군, A 처리군, B 처리군
② 모델 2. 임의효과 모델링(random effect modeling)
○ 정의 : 모집단이 가지는 일반적인 경향을 보는 것. 즉 factor의 level이 랜덤한 것
○ 방법 : 모집단에서 임의로 추출하여 ANOVA 분석을 하는 것. 사후검정 불요
○ 예 : 공장의 주인이 공장 생산품의 중량이 모두 같은지 확인하고자 하는 경우
③ 일원 분산분석에서 고정효과와 임의효과는 동일한 계산과정을 거침
⑶ 문제 상황
| 요인 | Group 1 | Group 2 | Group 3 |
| 표본 | 11 | 8 | 5 |
| 10 | 7 | 4 | |
| 8 | 5 | 2 | |
| 7 | 4 | 1 | |
| 평균 | 9 | 6 | 3 |
Table. 1. 일원배치 분산분석 예제
① X̄1 = 9, X̄2 = 6, X̄3 = 3, X̄ = 6
② Group 1, Group 2, Group 3의 샘플 크기가 달라도 됨
⑷ 가설 설정
① H0 : μGroup 1 = μGroup 2 = ··· = μGroup m = μ (단, 위 문제 상황에서 m = 3)
② H1 : 적어도 한 쌍의 모평균은 같지 않음
⑸ F 통계량 유도
① 발상 : 그룹 내 분산이 그룹간 분산보다 명백히 작은 경우 표본집단 간 차이가 있다고 말할 수 있음
② 정의
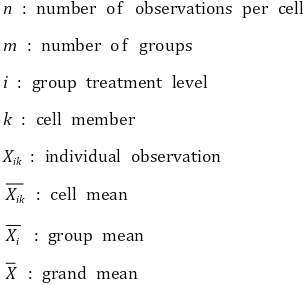
③ 제곱합(SS, sum of squares)

④ 분산비 계산
○ 분산비(variance ratio) : F 비(F ratio)라고도 함
○ 그룹 간 분산(among-group variance) : 오류(error) 및 처리 효과(treatment effect)와 관련 있음
○ 그룹 내 분산(within-group variance) : 오류(error)와 관련 있음
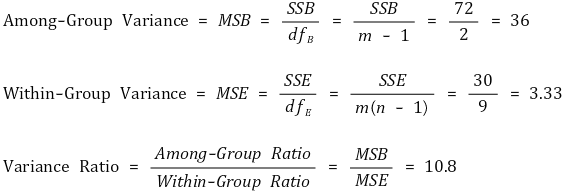
⑤ 결과표
| 요인 | 제곱합 | 자유도 | 평균제곱 | F 비 | p 값 |
| 효과 | 72 | 2 | 36 | 10.8 | 0.0040583 |
| 오차(잔차) | 30 | 9 | 3.33 | ||
| 합계 | 102 | 11 |
Table. 2. 결과표
○ 오차 제곱합 = among-group variance + within-group variance = 72 + 30 = 102
○ 전체 자유도 = among-group variance의 자유도 + within-group variance의 자유도 = (k - 1) + (n - k) = n - 1
○ Group 변수는 수치가 아니므로 결정계수 계산은 무의미함
○ 보고 예시 : "A single-factor ANOVA showed a significant difference among the three treatments (Group 1, Group 2, and Group 3): F2.9 = 10.8, p < 0.01"
○ 팁. 72, 30을 계산할 때 계산하는 항 수는 모두 12개임 (∵ 대칭성)
⑹ F 통계량 증명
① (참고) 표본집단과 표본분포
② 그룹 간 분산의 분포
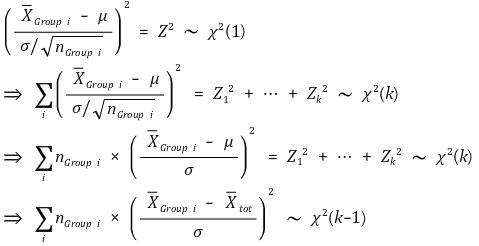
③ 그룹 내 분산의 분포
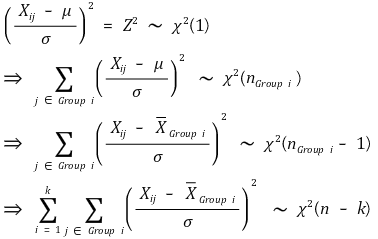
④ 분산 비의 분포
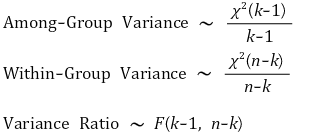
⑺ 특징
① 각 그룹의 샘플 개수가 비슷해야 검정력이 높음
② 특정 그룹의 샘플 개수가 적으면 신뢰성이 의심됨
③ 대립가설을 기각한다고 하여 항상 pairwise t testing에서 한 쌍의 평균이 다르다는 결론이 나오는 것은 아님
④ pairwise t testing이 아닌 다른 사후검정(post hoc analysis, posterior analysis)을 통해 어느 그룹이 다른지 알 수 있음
⑻ Levene test : 이분산성(heteroscedasticity) 검정법
① 1st. 각 표본집단 평균에 대한 편차 절대값을 그룹별로 조사
○ Control : (8, 7, 7, 8)
○ Tumostat : (2, 1, 1, 2)
○ Inhibin 4 : (2, 1, 1, 2)
② 2nd. 세 개의 새로운 그룹에 대해 one-way ANOVA를 실시
③ 3rd. Control이 다른 두 개의 그룹에 비해 확실하게 큰 편차를 보여주고 있음 : 등분산성(homoscedasticity) 기각
⑼ 사후검정 : 기본적으로 다중비교(multiple comparison)로부터 응용된 것
① LSD, Bonferroni, Sidak, Tukey, Duncan, Dunnett, Scheffe, Student-Newman-Keuls, BH procedure 등
○ Scheffe, Tukey, Duncan, Student-Newman-Keuls를 가장 많이 씀
○ 셋 중 Scheffe가 가장 보수적이고 Duncan이 가장 느슨함
○ 자연과학 기준 : 일반적으로 Tukey를 먼저 시도하고 유의하지 않으면 Duncan을 사용
○ 사회과학 기준 : 일반적으로 Scheffe를 자주 사용함
② 예 : Tukey HSD(Tukey test, honestly significant difference, Tukey-Kramer method)
○ (구별 개념) Bland-Altman 테스트
○ 통계량 : student T 분포를 이용

○ 검정
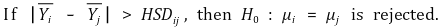
○ 상황 1. 표본평균이 A > B > C > D > E
○ 상황 2. one-way ANOVA 결과 모든 평균이 같지 않음
○ 1st. A-E, A-D, A-C, A-B 순으로 Tukey 통계량으로 검정 : A-C가 유의하지 않으므로 A-B 검정은 생략
○ 2nd. B-E, B-D, B-C 순으로 Tukey 통계량으로 검정 : A-C가 유의하지 않으므로 B-C 검정은 생략
○ 3rd. C-E, C-D 순으로 Tukey 통계량으로 검정
○ 4th. D-E를 Tukey 통계량으로 검정
○ 크기순으로 정렬하지 않으면 총 10번을 검정하여 10번의 1종 오류가 누적
○ 위의 경우 8번의 1종 오류가 누적돼 약간 더 나은 상황
③ 사후검정 시 주의할 점
○ 예제
| Control | Neurohib | Mitostep |
| 7 | 4 | 1 |
| 8 | 5 | 2 |
| 10 | 7 | 4 |
| 11 | 8 | 5 |
Table. 3. 사후검정 예제
○ 결과
Figure. 4. 사후검정 주의사항
○ Control = Neurohib, Neurohib = Mitostop인데 Control ≠ Mitostop인 것은 제1종 오류 때문
○ 예 : A = B일 확률이 10%이고 B = C일 확률이 10%이면 A = B = C일 확률은 1%로서 유의하게 차이 있음
3. 이원배치 분산분석(two-way ANOVA) [목차]
⑴ 개요
① 정의 : 두 가지 독립변인, 한 가지 종속변인에 대해 분산분석을 시도하는 것
② 각 요인의 주효과(main effect)뿐만 아니라 이들의 상호작용도 관심대상임
③ 가정
○ 정규성 : 모집단들은 정규분포를 따름
○ 독립성 : 모집단으로부터 무작위적으로 표본을 추출함
○ 등분산성 : 모집단들은 동일한 분산을 가짐
○ 직교성(orthogonality) : 두 개의 요인이 서로 상관관계가 없을 것
○ 직교성을 만족함은 상호작용이 없음과 전혀 관련이 없음 : 개념의 차이를 이해해야 함
⑵ 상황 분류
Figure. 5. 두 가지 요인에 대한 실험결과 분류
⒜ 온도 효과 없음, 습도 효과 없음
⒝ 온도 효과 없음, 습도 효과 있음
⒞ 온도 효과 있음, 습도 효과 없음
⒟ 온도 효과 있음, 습도 효과 있음
⒠ 온도 효과 있음, 습도 효과 있음, 상호작용 있음
⑶ 이원 분산분석 모델
① 이원배치 분산분석에서 임의효과의 경우 다르게 계산돼야 하는 이유
Figure. 6. 이원배치 분산분석에서 임의효과의 경우 다르게 계산돼야 하는 이유
○ 상황 : B2, B4는 factor B에서 임의로 추출한 level
○ 예상 : A의 주효과가 모호해야 함
○ 실제 : 임의추출 효과로 인해 A의 주효과가 있는 것처럼 보임
② 모델 1. 고정효과 모델링(fixed effect modeling) : 두 factor의 level이 정해져 있는 것
| 요인 | 제곱합 | 자유도 | 평균제곱 | F 비 |
| A | SSA | dfA = I-1 | MSA = SSA ÷ dfA | FA = MSA ÷ MSE |
| B | SSB | dfB = J-1 | MSB = SSB ÷ dfB | FB = MSB ÷ MSE |
| A × B | SSA×B | dfA×B = (I-1)(J-1) | MSA×B = SSA×B ÷ dfA×B | FA×B = MSA×B ÷ MSE |
| 오차(잔차) | SSE | dfE = n-IJ | MSE = SSE ÷ dfE | |
| 총합 | SST | n-1 |
Table. 4. 고정효과 모델링 결과표 (ref)
③ 모델 2. 임의효과 모델링(random effect modeling) : 두 factor의 level이 랜덤한 것
| 요인 | 제곱합 | 자유도 | 평균제곱 | F 비 |
| A | SSA | dfA = I-1 | MSA = SSA ÷ dfA | FA = MSA ÷ MSA×B |
| B | SSB | dfB = J-1 | MSB = SSB ÷ dfB | FB = MSB ÷ MSA×B |
| A × B | SSA×B | dfA×B = (I-1)(J-1) | MSA×B = SSA×B ÷ dfA×B | FA×B = MSA×B ÷ MSE |
| 오차(잔차) | SSE | dfE = n-IJ | MSE = SSE ÷ dfE | |
| 총합 | SST | n-1 |
Table. 5. 임의효과 모델링 결과표 (ref)
④ 모델 3. 혼합효과 모델링(mixed effect modeling) : 한 factor의 level은 정해져 있고 다른 factor의 level은 랜덤한 것
| 요인 | 제곱합 | 자유도 | 평균제곱 | F 비 |
| A | SSA | dfA = I-1 | MSA = SSA ÷ dfA | FA = MSA ÷ MSA×B |
| B | SSB | dfB = J-1 | MSB = SSB ÷ dfB | FB = MSB ÷ MSE |
| A × B | SSA×B | dfA×B = (I-1)(J-1) | MSA×B = SSA×B ÷ dfA×B | FA×B = MSA×B ÷ MSE |
| 오차(잔차) | SSE | dfE = n-IJ | MSE = SSE ÷ dfE | |
| 총합 | SST | n-1 |
Table. 6. 혼합효과 모델링 결과표 (ref)
○ A가 고정효과이고 B가 임의효과인 상황
○ 팁. 아래 지분분산분석 예제와 비교하면서 이해할 것
⑷ 예제 : 고정효과 모델링
| Humidity (%) | Temperature (℃) | ||
| 20 | 30 | 40 | |
| 33 | 1 | 5 | 9 |
| 2 | 6 | 10 | |
| 3 | 7 | 11 | |
| 66 | 9 | 13 | 17 |
| 10 | 14 | 18 | |
| 11 | 15 | 19 | |
| 99 | 17 | 21 | 25 |
| 18 | 22 | 26 | |
| 19 | 23 | 27 | |
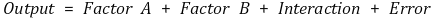
① 정의

② 제곱합(sum of squares)

③ 분산비 계산
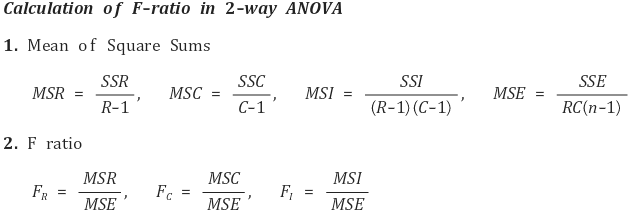
④ 결과표
| 요인 | 제곱합 | 자유도 | 평균제곱 | F 비 | p 값 |
| 온도 | 288 | 2 | 144 | 144 | 8.43e-12 |
| 습도 | 1152 | 2 | 576 | 576 | < 2e-16 |
| 온도 × 습도 | 0 | 4 | 0 | 0 | 1 |
| 오차(잔차) | 18 | 18 | 1 | ||
| 합계 | 1464 | 26 |
Table. 8. 결과표
○ 귀무가설 1. μ20℃ = μ30℃ = μ40℃ = μ : p value = 8.43e-12 < 0.05이므로 기각
○ 귀무가설 2. μ33% = μ66% = μ99% = μ : p value < 2e-16 < 0.05이므로 기각
○ 귀무가설 3. 온도와 습도의 상호작용 = 0 : p value = 1이므로 인용
○ 결정계수 = 1 - 18 ÷ 1464 = 0.987704918
○ 상관계수 = ± √ 0.987704918 = 0.993833445
○ 기울기의 추정량의 부호에 따라 상관계수의 부호가 결정됨
⑤ 상호작용은 주효과를 모호하게 하므로 유의한 상호작용이 있을 때 F 값을 믿으면 안 됨
○ 예를 들어 물질 A는 유전자 발현을 촉진하고 물질 B는 유전자 발현을 억제하는 경우
○ 물질 A와 물질 B를 동시에 처리하면 유전자 발현에 큰 변화가 없음
○ 그렇지만 A, B 모두 효과가 없는 게 아님
⑸ 응용 1. 반복이 없는 테스트(test without replication)
① 개요
○ 일원배치 분산분석에서는 불가능
○ 실험 개체수가 부족하거나 비용이 많이 드는 경우에 사용
② 예시
| Radiation Level | Drug | 평균 | ||
| Proshib | Testosblock | Control | ||
| Low | 81 | 76 | 79 | 78.67 |
| Medium | 45 | 46 | 45 | 45.33 |
| High | 28 | 27 | 27 | 27.33 |
| 평균 | 51.33 | 49.67 | 50.33 | 50.44 |
③ 결과표
| 요인 | 제곱합 | 자유도 | 평균제곱 | F 비 | p 값 |
| Drug | 4070.222 | 2 | 2035.111 | 832.546 | 5.74e-06 |
| Radiation | 4.222 | 2 | 2.111 | 0.864 | 0.488 |
| 오차(잔차) | 9.778 | 4 | 2.444 | ||
| 합계 | 4084.222 | 8 |
Table. 10. 반복이 없는 분산분석 결과표
○ 반복이 없는 분산분석은 상호작용 항을 절대 포함시키면 안 됨
○ 상호작용 항을 포함시키면 잔차의 자유도 = (RC - 1) - (R - 1 + C - 1 + (R - 1)(C - 1)) = 0이 되어 F 비 계산 불가
⑹ 응용 2. 임의 블록 실험설계(randomized block experimental design) : 반복이 없는 분산분석의 예시
① 정의 : 지역을 여러 개의 블록으로 나눈 뒤, 각 블록을 다시 세분화하여 특정 요인에 대해 상이하게 실험
○ 이원배치 분산분석 가능 : 블록의 지역 특이적 요인과 treatment 요인의 두 가지 요인
○ 목적 : 지역 특이적 요인을 분리하여 treatment의 통계적 결론의 신뢰성을 높이기 위함
② 과정
○ 1st. 전체 지역을 여러 가지 지역으로 나눔
○ 2nd. 각 지역에 블록 넘버를 임의로 배정
○ 3rd. 각 블록을 treatment의 level의 수만큼 서브 블록으로 나눔
○ 4th. 서브 블록에서 treatment의 level의 위치를 랜덤하게 할당
○ 5th. 각 블록 내 각 treatment에 대해 반복측정을 함
○ 6th. 블록 요인이 유의성을 보이면 지역 특이적인 요인이 분명하게 존재했음을 알 수 있음
○ 지역 특이적인 요인 : 지하수의 존재 유무, 일광의 차이, 지하 광맥의 유무 등
③ 결과
⑺ 응용 3. 지분 분산분석(nested analysis of variance)
① 유사 이원 분산분석 : 실제로는 일원 분산분석으로 분류됨
② 예제
○ 문제 상황
| Prawn Food + Vitamin A | Prawn Food | ||
| Pond 1 | Pond 2 | Pond 3 | Pond 4 |
| 30 | 60 | 80 | 110 |
| 35 | 65 | 85 | 115 |
| 45 | 75 | 95 | 125 |
| 50 | 80 | 100 | 130 |
○ F 통계량 계산
| 요인 | 제곱합 | 자유도 | 평균제곱 | F 비 | p 값 |
| Diet | 10000.0 | 1 | 10000.0 | 5.556 | 0.143 |
| Pond(Diet) | 3600.0 | 2 | 1800.0 | 21.600 | 0.000 |
| 오차(잔차) | 1000.0 | 12 | 83.3 | ||
| 합계 | 14600.0 | 14 |
Table. 13. 지분 분산분석 F 통계량 계산
○ 실제 계산 : 10000, 3600, 1000을 계산할 때 우변의 항 수는 모두 16개임 (∵ 대칭성)
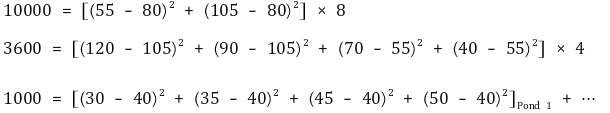
③ 임의 블록 실험 설계와 유사해 보이지만 분명한 차이점이 존재
○ 차이 1. Pond 1, Pond 2, Pond 3, Pond 4를 어떤 블록으로 분류할 수 없음
○ 차이 2. 기본적으로 이원 분산분석의 가정인 직교성을 만족하지 않음 : Diet와 Pond(Diet)는 orthogonal하지 않음
○ 차이 3. 자유도 계산이 다름 : Pond(Diet)의 자유도는 Pond 1 ↔ Pond 2와 Pond 3 ↔ Pond 4로 총 2임
○ 위 예제에서 임의 블록 실험 설계를 하는 경우 블록에 대한 자유도는 1임
○ 임의 블록 실험 설계는 오차의 자유도를 증가시켜서 F 비가 증가함 (검정력 증가)
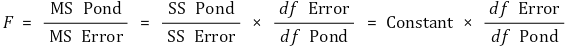
○ 지분 분산분석이 아니라 임의 블록 실험 설계를 지향하는 이유
○ 차이 4. Pond(Diet)를 독립적인 factor로 보지 않고 Pond × Diet처럼 계산
입력: 2019.11.16 17:36
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 3-2강. 몬티홀 문제 (0) | 2019.07.03 |
|---|---|
| 【통계학】 3-1강. 포함배제의 원리 (0) | 2019.06.27 |
| 【통계학】 14강. 통계적 검정 (0) | 2019.06.19 |
| 【통계학】 13강. 통계적 추정 (0) | 2019.06.19 |
| 【통계학】 11강. 표본집단과 표본분포 (0) | 2019.06.19 |













최근댓글