13강. 통계적 추정
추천글 : 【통계학】 통계학 목차
1. 개요 [목차]
⑴ 통계적 추정 : 표본을 통해 모집단의 특성을 추정하는 것
⑵ 상태공간(state space) : ℝn. 목격하는 표본(샘플)들을 모두 모아놓은 집합
2. 점추정(point estimation, parametric approach, location type) [목차]
⑴ 정의 : 표본 (x1, ···, xn)을 보고 모수를 추정하는 방법

① 모수(parameter) : 모집단의 특성을 보여주는 값. μ, σ, θ, λ 등
② μ : 모집단의 평균
③ σ : 모집단의 표준편차
④ θ : 베르누이분포 혹은 이항분포에서 성공확률
⑤ λ : 푸아송분포 혹은 지수분포의 λ
⑵ 표본분포(empirical distribution, sampling distribution)
⑶ 점추정량(point estimator) : 모수 θ에 대해
① 정의 1. 점추정량은 하나의 수치가 아니라 함수임
② 정의 2. 점추정량은 X1, ···, Xn에 대한 함수

③ 정의 3. 점추정량의 확률은 θ에 대한 함수임

⑷ 좋은 점추정량의 기준
① 기대제곱오차(mean squared error, MSE) : model risk라고도 함
○ bias-variance decomposition
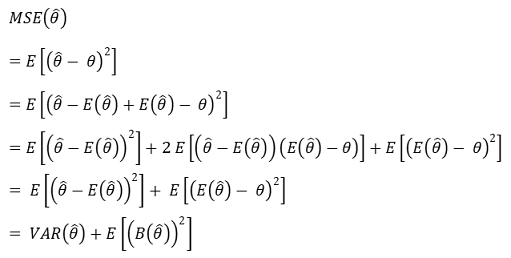
○ bias와 chance error의 공분산이 직관적으로 0임을 이용하여 중간항을 제거
○ bias을 줄이는 전략은 model variance를 증가시킴
○ model variance을 줄이는 전략은 bias를 증가시킴
② 기준 1. 편향(bias) : systemic error, non-random error, model bias라고도 함
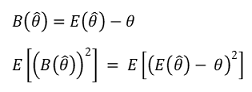
○ 편향이 작을 것이 요구됨
○ 원인 : 언더피팅(underfitting), 도메인 지식(domain knowledge)의 부족
○ 해결방법 : 더 복잡한 모델의 사용, 도메인에 적합한 모델의 사용
○ 불편추정량(unbiased estimator) : B = 0 ⇔ 표본평균 = 모평균. 불편성(unbiasness)이 있으면 좋은 추정량
○ 예 1. 표본평균(sample mean) : 모평균의 불편추정량
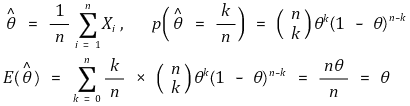
○ 예 2. 표본분산(sample variance) : 모분산의 불편추정량
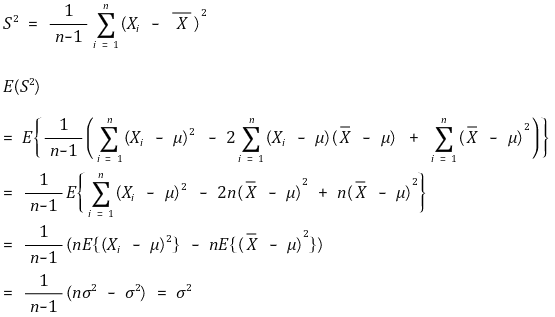
○ 예 3. 표본공분산(sample covariance)
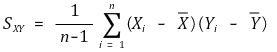
○ 예 4. Xi ~ u[0, θ]일 때, 불편추정량인 경우와 불편추정량이 아닌 경우
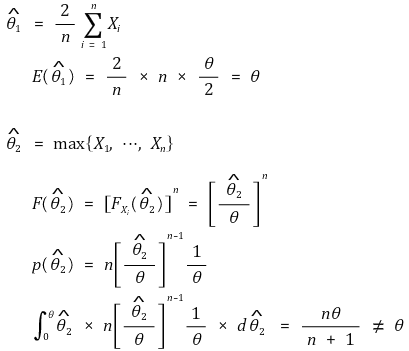
③ 기준 2. 유효성(efficiency) : 랜덤한 chance error와 관련

○ 불편추정량이라는 전제 하에서 분산이 작을 것이 요구됨
○ 2-1. noise variance : 1st chance error, observation variance라고도 함. σ2과 같이 표시
○ 예 : 측정 기기 자체의 에러, 측정 대상 자체의 노이즈
○ 이들 정보를 측정하려는 시도도 있으나 굉장히 어려움이 많음
○ 2-2. model variance : 2nd chance error라고도 함
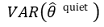
○ 표본집단은 모집단으로부터 무작위 추출된 집합이라는 점에서 기인한 chance error
○ 원인 : 오버피팅(overfitting)
○ 해결방안 : 더 단순한 모델의 사용
○ bias-variance tradeoff : 모델 복잡도가 증가할수록 bias가 감소하나 model variance가 증가해 트레이드오프 관계 및 최적 복잡도가 존재함
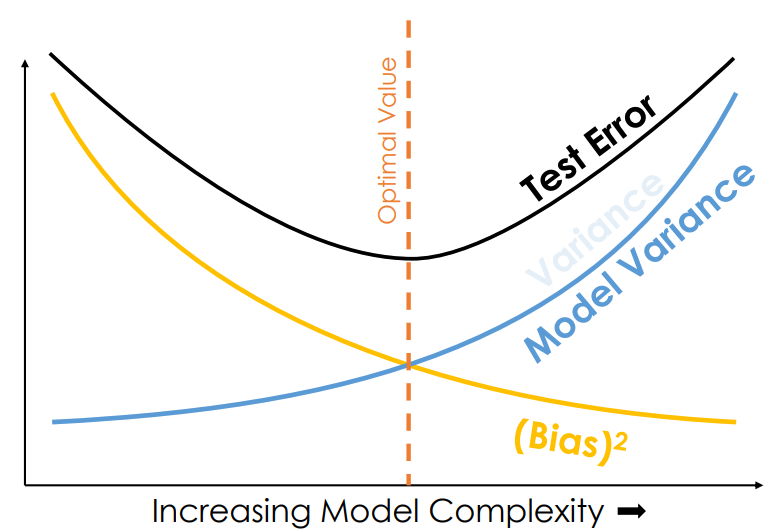
Figure. 1. bias-variance tradeoff
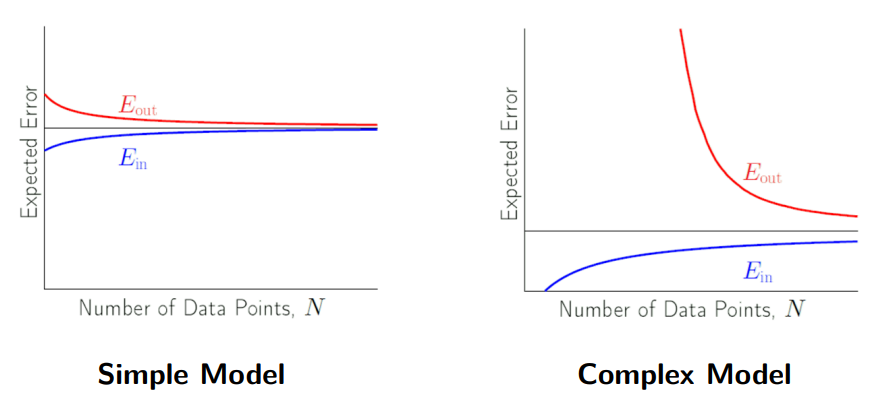
○ BLUE(best linear unbiased estimator) : 선형 불편추정량 중 가장 분산이 작은 것
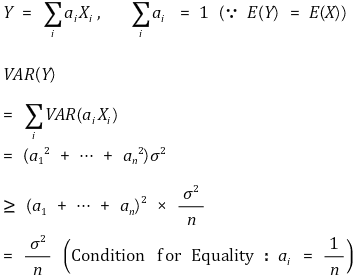
○ 균일최소분산불편추정량(UMVU, uniformly minimum variance unbiased)
○ 정의 : 불편추정량(비선형 포함) 중 가장 분산이 작은 것
○ 피셔정보(Fisher information) In의 직접 계산
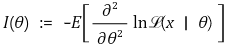
○ 피셔정보(Fisher information) In의 간접 계산
○ 크라메르-라오 하한(Cramér–Rao lower bound) = 1 / In
○ 어떤 추정량이 분산이 크라메르-라오 하한과 같으면 UMVU임
○ 예 1. 표본평균과 표본중위수
○ 모분포가 정규분포일 때 표본평균의 점근적 분포
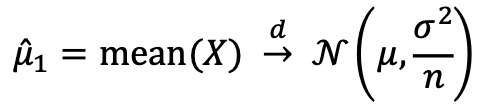
○ 모분포가 정규분포일 때 표본중위수의 점근적 분포

○ 모분포가 정규분포일 때, Hodges-Lehmann = median[(Xi + Xj) / 2 : i ≤ j]는 표본평균보다 더 efficient
○ 확률변수가 double-exponential 분포에서 오면 표본평균이 표본중위수보다 분산이 더 큼
○ 예 2. 표본표준편차(Sn)와 MAD(median absolute deviation)
○ Sn →d σ
○ MAD = median(|X1 - μ|, ⋯, |Xn - μ|) →d Φ-1(3/4) σ = 0.676 σ
④ 기준 3. 일관성(consistency)과 일치추정량(consistent estimator)
○ 점근적 특성(asymptotic property) : 표본크기(sample size)가 ∞로 접근할 때의 특성
○ 점근적 불편성(asymptotic unbiasedness) : n → ∞일 때 불편성을 만족하는 경우. 큰 수의 법칙과 관련
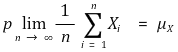
○ 점근적 효율성(asymptotic efficiency)
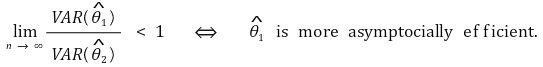
○ 일관성 : 추정량이 모수로 수렴하는 성질
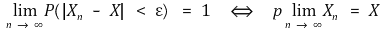
○ X는 확률변수지만, 일반적으로 특정 상수로 생각
○ 예 : 다음은 일관성이 없어 좋지 않은 확률변수임
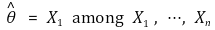
○ ARE(asymptotic relative efficiency) : 두 확률변수의 점근적 분포의 분산의 비율. 이론값과 다르면 이상치의 존재를 암시
⑤ 기준 4. robust estimator : 이상치에 더 민감한지를 조사
⑥ 기준 5. least squared estimator : 표본평균은 least squared estimator
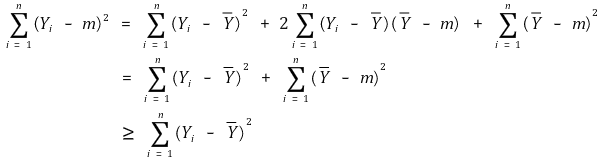
⑸ 방법 1. 이산확률분포와 최대 확률
① 이항계수의 정의를 이용
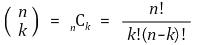
② 예제
○ 상황 : 표지-재포획법을 통한 개체수(N) 추정
○ 개체수 N, 최초 포획 개체수 m, 나중 포획 개체수 n, 나중 표지 개체수 x
○ 확률분포 : 초기하분포(hypergeometric distribution)
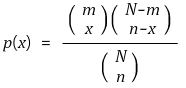
○ 문제 : 가장 합리적인 N 값
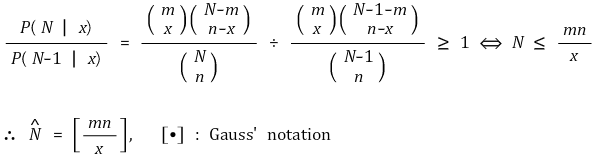
⑹ 방법 2. 적률방법(MOM, method of moment estimator), 표본유사 추정(sample analog estimation)
① 정의 : E(Xk) = g(θ) ⇔ θ = g-1(E(Xk))가 성립하므로, θ의 추정량 = g-1((1/n) × ∑Xik)로 설정하는 방법
○ E(Xk) : 적률(moment) 또는 모집단 적률(population moment)
○ (1/n) × ∑Xik : 표본적률(sample moment)
○ 적률은 하나의 상수이고, 표본적률은 일정한 분포를 갖는 확률변수임
○ 일관성(consistency) : 큰수의 법칙에 의해 표본적률은 적률로 수렴
② 표본적률(sample moment)
○ 원점에 대한 k차 표본적률
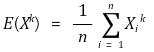
○ 표본평균에 대한 k차 표본적률
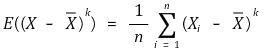
③ 예제
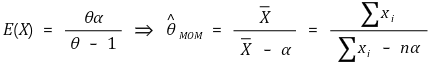
⑺ 방법 3. 최대우도 추정(ML, maximum likelihood method)
① 정의
○ θ : 모수(parameter)
○ θ* : 모수의 추정량
○ θML : 모수의 최대우도 추정량
② 우도(likelihood) : 어떤 일이 발생할 가능성
③ 우도함수(likelihood function)
○ θ*가 주어져 있을 때 주어진 표본이 나올 확률
○ 우도의 곱(product of likelihoods)이라고도 함
○ 즉, p(X | θ*)
○ ℒ로 표시
④ 로그우도함수 : 우도함수에 로그를 취한 것
○ ℓ = ln ℒ로 표시
⑤ 최대우도 추정(maximum likelihood estimation; MLE) : 우도함수 p(X | θ)가 최대가 되는 θML을 조사하는 것
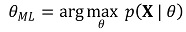
○ 가정 : 추정량 θ*가 모수 θ와 가까울수록 우도함수가 더 커질 것임
○ 1st. 로그우도함수 미분 : 유효한 구간에서 극댓값을 만드는 θ* 조사
○ 2nd. 극댓값 존재 : 극댓값을 만드는 θ*가 θML이라고 추정
○ 3rd. 극댓값 부존재 : 양 말단 중 더 높은 우도를 갖는 θ*가 θML이라고 추정
○ 최대우도 추정과 헤세 행렬 및 테일러 전개 : 미분가능한 모든 함수의 추정량을 구할 수 있는 유용한 방법
○ 단계 1. θk에 대하여 테일러 급수를 구하여 2차 근사식을 구하고 근사식의 극대해 θk+1 = θk + dk를 구함
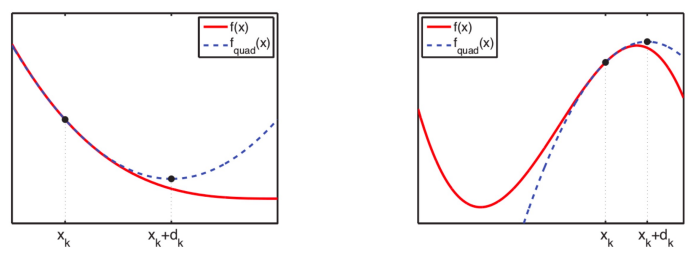
Figure. 3. 최대우도 추정과 테일러 전개와의 관계
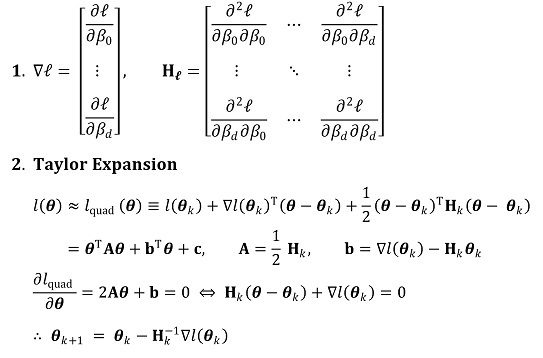
○ 단계 2. 뉴턴-랩슨법(Newton-Raphson method)처럼 θk를 업데이트하면 결국 global maximum에 도달
○ 예시 : logistic regression
⑥ 최대우도 추정량 : 표본 X가 주어졌을 때 우도를 최대로 만드는 θML과 대응시키는 함수 G
○ θML = Gℓ (ℓ) = Gℒ (ℒ)
○ 추정량의 한계 : 최대우도 추정 시 썼던 가정에 한계가 있음
○ (참고) 통계학자들이 선호하는 추정량
⑦ MAP(maximum a posteriori)
○ 최대우도 추정은 Bayes rule의 특수한 예

○ MLE는 파라미터의 균일 분포를 가정하지만, 사전(piror) 분포가 있는 경우에는 MAP 방법을 사용
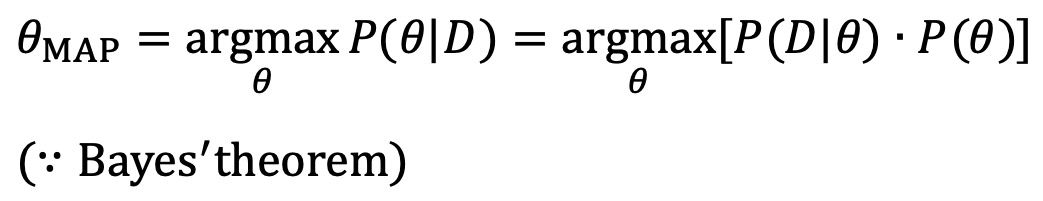
⑧ 예 1.
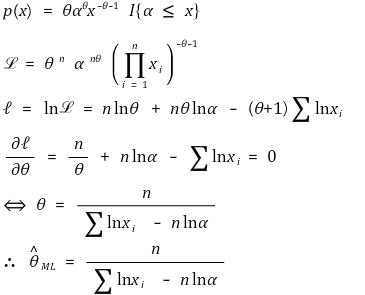
⑨ 예 2.
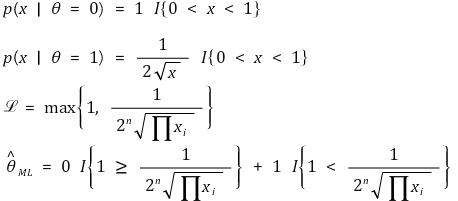
⑩ 예 3.
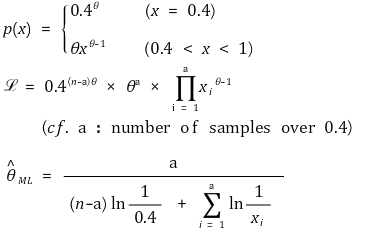
⑪ 예 4. 최대우도 추정이 유일하게 결정되지 않을 수 있음

⑫ 성질 1. 일관성(consistency)
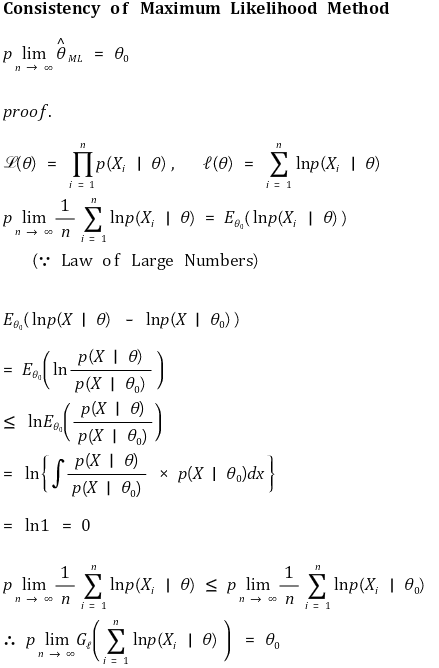
⑬ 성질 2. 점근적 정규분포(asymptotic normal distribution)

⑭ 성질 3. 불변성(invariance) : θML이 θ의 최대우도 추정량이면, g(θML)은 g(θ)의 최대우도추정량임
3. 구간추정(interval estimation, scaling type) [목차]
⑴ 정의 : 표본들을 통해 모수가 어떤 구간에 있는지를 추정하는 것
① 도입취지 : 점추정량이 실제 모수와 정확히 일치할 가능성은 0임
② 신뢰도(신뢰계수)
○ P(θleft < θ < θright) = 1 - α, 0 < α < 1
○ 임계치 : 신뢰구간의 경계를 구성하는 값. θleft, θright 등
○ 1 - α : 신뢰도(confidence level, confidence coefficient)
○ α : 기각확률(rejection probability) 또는 유의수준(significance level)
○ 신뢰구간(confidence interval) : θ가 놓일 확률이 (1 - α) × 100 %인 [θleft, θright]를 의미
③ 필수 암기사항
○ P(Z > 1.65) = 5% ⇔ P(|Z| > 1.65) = 10%
○ P(Z > 1.96) = 2.5% ⇔ P(|Z| > 1.96) = 5%
○ P(Z > 2.58) = 0.5% ⇔ P(|Z| > 2.58) = 1%
④ 68 - 95 - 99.7 rule
○ μ ± 1 × σ : 68.27 %
○ μ ± 2 × σ : 95.45 %
○ μ ± 3 × σ : 99.73 %
⑵ 경우 1. Xi ~ N(μ, σ2)이고 모분산(σ2)을 알고 있는 경우
① 개요 : 정규분포 이용
② 방법
○ 도입 : μ를 알 때 Xavg의 확률 (신뢰도 : α)
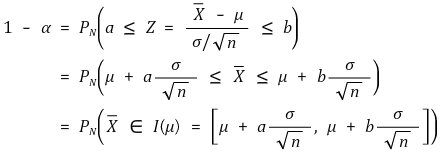
○ 발상의 전환 : Xavg ∈ I (μ) ⇔ μ ∈ I (Xavg) (신뢰도 : α)
○ 의미 : Xavg를 알 때 μ의 확률분포
○ μ의 확률분포가 μ를 알 때 Xavg의 확률분포와 동일한 개념틀로 설명된다는 것을 이해해야 함
○ 직접 그림을 그려서 확인해 보기
Figure. 4. μ를 알 때 Xavg의 분포와 Xavg를 통해 추측한 μ의 신뢰구간이 동일함을 보여주는 그림
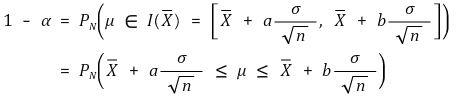
○ 중심축 결정(pivotal estimation) : 신뢰구간의 길이가 짧으려면 |a| = |b|, 즉 a = - zα/2, b = zα/2여야 함 (증명생략)
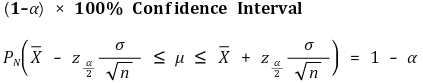
③ (참고) 분포함수를 아는 경우
○ 예 1. F(x) = √x / θ, 0 ≤ x ≤ θ2 : 90% 신뢰구간은 다음과 같음

○ 예 2. F(x) = (x / θ)n : 90% 신뢰구간은 다음과 같음
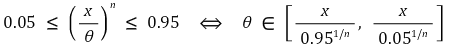
⑶ 경우 2. Xi ~ N(μ, σ2)이고 모분산(σ2)을 모르는 경우
① 개요
○ 정규분포는 모집단의 분산을 알아야 함
○ 현실적으로 모집단의 분산을 모르기 때문에 표본분산을 사용
○ 모분산 대신 표본분산을 사용시 표본평균의 분포가 바로 T-분포임
② 예 1. 표본평균
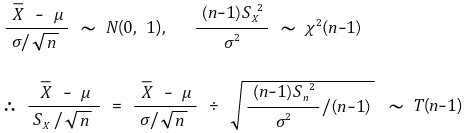
○ 도입 : μ를 알 때 Xavg의 확률 (신뢰도 : α)
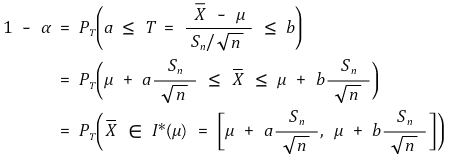
○ 발상의 전환 : Xavg ∈ I* (μ) ⇔ μ ∈ I* (Xavg) (신뢰도 : α)
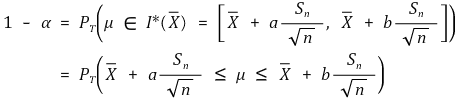
○ 중심축 결정(pivotal estimation) : 신뢰구간의 길이가 짧으려면 |a| = |b|, 즉 a = - tα/2, b = tα/2여야 함 (증명생략)
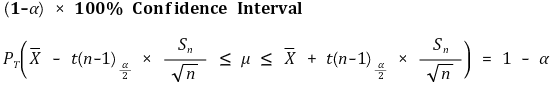
③ 예 2. (case 1) Xi (μX, σ2) (i = 1, ···, n)와 Yj (μY, σ2) (i = 1, ···, n)가 대응표본인 경우
○ 대응표본 검정(paired estimation, matched sample estimation)이라고 함
○ 사실상 변수가 하나임 : Wi = Xi - Yi로 정의한 뒤 예 1을 적용
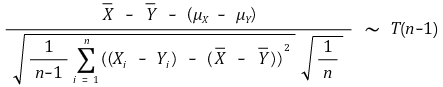
○ 대응표본의 예
○ 독립표본의 예
④ 예 3. (case 2) 표본평균의 차 : Xi (μX, σ2) (i = 1, ···, n)와 Yj (μY, σ2) (j = 1, ···, m)가 독립일 때
○ 이표본추정(unpaired sample estimation, pooled sample estimation) 중 분산이 같은 경우
○ 수식화
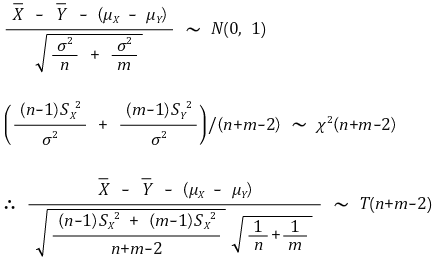
○ 신뢰도 α의 신뢰구간
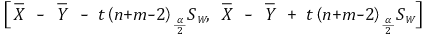
⑤ 예 4. (case 3) 표본평균의 차 : Xi (μX, σX2) (i = 1, ···, n)와 Yj (μY, σY2) (j = 1, ···, m)가 독립일 때 (단, σX ≠ σY)
○ 이표본추정(unpaired sample estimation, pooled sample estimation) 중 분산이 다른 경우
○ Welch Approach 이용
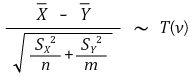
○ (case 2)보다 자유도가 낮음 → 검정력이 감소
○ (참고) ν의 수식은 굉장히 복잡함
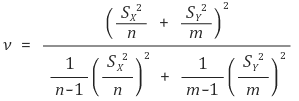
⑥ 예 5. 모분산의 신뢰구간
○ 신뢰구간의 크기를 최소화하는 명료한 해가 없음을 유의 : 수치해석을 이용해야 함
○ 주어진 모델
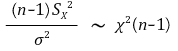
○ 신뢰도 α의 신뢰구간

⑦ 예 6. 모분산의 비
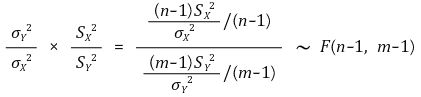
○ 신뢰도 α의 신뢰구간
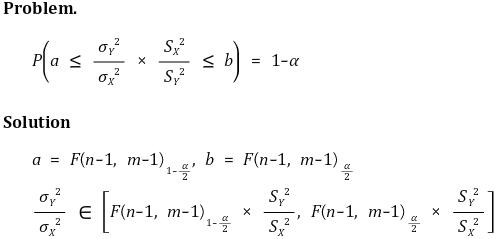
⑷ 경우 3. 표본이 정규분포를 따르지 않으나 표본이 많은 경우
① 중심극한정리 : n이 충분히 크면 표본평균의 분포는 정규분포로 수렴
○ 수식화
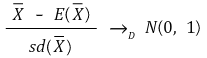
○ T 분포도 결국 정규분포로 수렴
② 표본개수
○ 일반적으로 25 ~ 30개의 표본만 있어도 정규성을 보임
○ symmetric unimodal (극대값 1개) 분포인 경우 n = 5인 것으로 충분
③ 예 1. 모비율
○ 주어진 모델
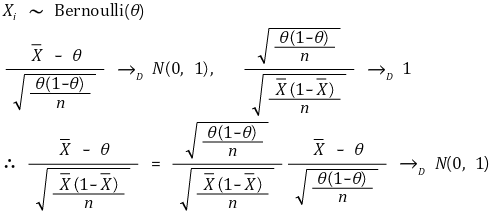
○ 신뢰도 α의 신뢰구간
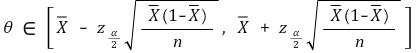
④ 예 2. 상관계수(correlation coefficient)
○ 귀무가설 H0 : 상관계수 = 0
○ 대립가설 H1 : 상관계수 ≠ 0
○ t 통계량 계산 : 표본으로부터 얻은 상관계수 r에 대하여,
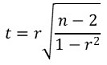
○ 위 통계량은 자유도가 n - 2인 student t 분포를 따름 (단, 샘플의 개수를 n이라고 가정)
입력: 2019.06.19 14:23
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 15강. 분산분석(ANOVA) (5) | 2019.06.21 |
|---|---|
| 【통계학】 14강. 통계적 검정 (0) | 2019.06.19 |
| 【통계학】 11강. 표본집단과 표본분포 (0) | 2019.06.19 |
| 【통계학】 8강. 확률변수변환 (0) | 2019.06.19 |
| 【통계학】 10강. 통계학 주요 정리 2부 (0) | 2019.06.18 |







최근댓글