8강. 확률변수변환(random variable transformation)
추천글 : 【통계학】 통계학 목차
1. 개요 [목차]
⑴ 확률변수변환 : Y = f(X)가 있고 pX(x)를 알고 있을 때, pY(y)를 구하는 방법론
⑵ 종류 1. 적률생성함수기법(moment generating function technique)
⑶ 종류 2. 분포함수기법(distribution function technique) : 2-step method
⑷ 종류 3. 변환기법(transformation technique) : 1-step method
2. 적률생성함수기법 [목차]
⑴ 정의

⑵ 적률생성함수와 확률분포는 일대일대응
⑶ 예제 : X ~ N(μ, σ2)이면 Y = aX + b ~ N(aμ + b, a2σ2)


3. 분포함수기법 [목차]
⑴ 정의
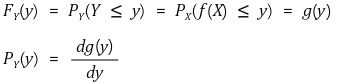
⑵ 예제 1. X ~ u[-1, 1], Y = X2
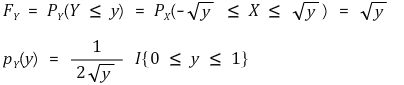
⑶ 예제 2. Y = max{X1, ···, Xn}, Xi : i.i.d.
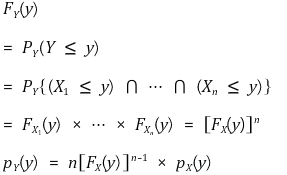
⑷ 예제 3. Y = min{X1, ···, Xn}, Xi : i.i.d.
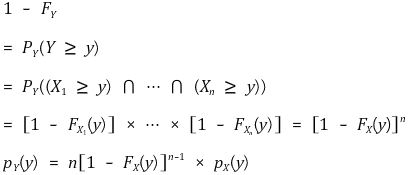
4. 변환기법 [목차]
⑴ 전제
① 일대일대응일 때 가능한 방법
② 전제조건에 의해 Y = u(X), X = ω(Y)인 함수 u, ω가 존재
⑵ 이산확률변수의 변환기법
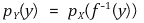
⑶ 연속확률변수의 변환기법
① 개요
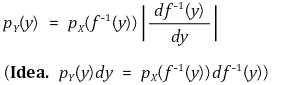
○ ω(Y)가 단조증가함수일 때
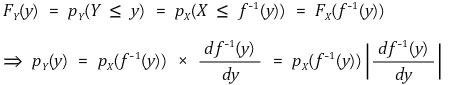
○ ω(Y)가 단조감소함수일 때
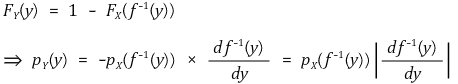
② 확장
○ 야코비안(Jacobian) : 함수행렬식의 일종. 기하학적으로 면적확대율을 의미
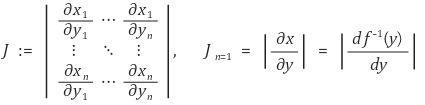
○ x1 = f1-1(y1, y2), x2 = f2-1(y1, y2)에 대해,
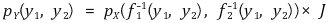
○ J ≠ 0이면 일대일대응이 성립
③ (중요) 일대일대응을 우회하는 방법
○ 전제 : pX(x) = e-x (x > 0), pY(y) = e-y (y > 0), Z = X + Y
○ 문제 : pZ(z)
○ 계산
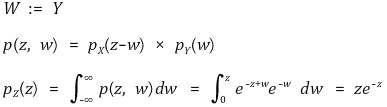
입력 : 2019.06.19 11:39
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 13강. 통계적 추정 (0) | 2019.06.19 |
|---|---|
| 【통계학】 11강. 표본집단과 표본분포 (0) | 2019.06.19 |
| 【통계학】 10강. 통계학 주요 정리 2부 (0) | 2019.06.18 |
| 【통계학】 9강. 통계학 주요 정리 1부 (0) | 2019.06.18 |
| 【통계학】 7강. 연속확률분포 (1) | 2019.06.16 |




최근댓글