10강. 통계학 주요 정리 2부
추천글 : 【통계학】 통계학 목차
1. 복원추출에서 표본표준편차 계산 [목차]
⑴ 정리
모집단에서 추출한 표본들 X1, X2, ···, Xn에 대하여 표본표준편차를

이 아니라

으로 정의하는 이유는 무엇일까? 표본집단 ≠ 모집단일 때 모평균 m을 추정할 때 모표준편차 σ의 값을 모르는 것이 보통이므로, 모표준편차를 표본표준편차로 대신할 수 있다고 하였다. σ를 대신하기에 Sn과 S 중 어느 것이 더 적절한지 생각하자.
⑵ 증명
다음은 Sn2의 기댓값 E(Sn2)을 구한 것이다.
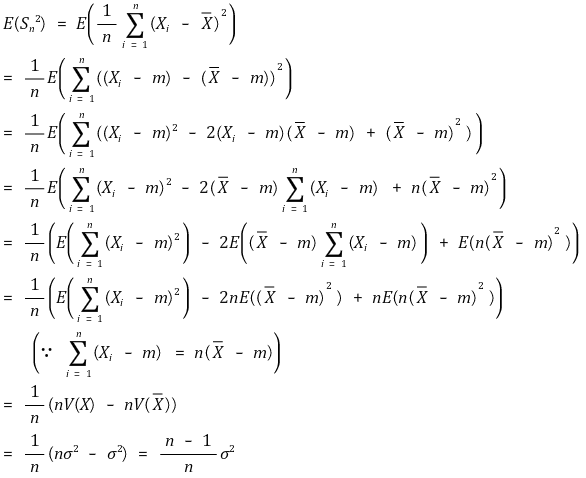
E(Sn2) = (n -1)/n × σ2이므로 Sn2은 모집단의 분산 σ2보다 작아지는 경향이 있다. Sn2에 n/(n - 1)을 곱한 S2의 기댓값은
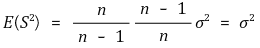
이므로, S2이 Sn2보다 모분산을 대신하기에 더 적절하다.
2. 비복원추출에서 표본표준편차 계산 [목차]
⑴ 정리
크기가 N이고, 모평균이 m, 모분산이 σ2인 모집단에서 크기 n인 표본을 비복원추출할 때, 표본평균의 분산은
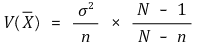
임을 증명하시오.
⑵ 증명
모집단의 변량들을 각각 a1, a2, ···, aN이라 하자. bi = ai - m이라 두면, 다음과 같다.
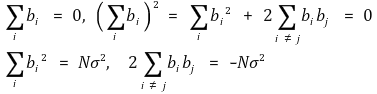
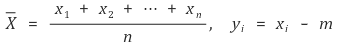
으로 정의하면 모집단에서 크기 n인 표본 x1, x2, ···, xn을 비복원추출했을 때, 가능한 모든 표본평균에 대하여 각각의 ai는 N-1Cn-1번 등장한다. 따라서
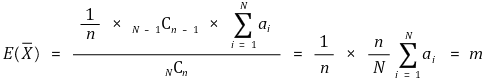
표본평균의 분산은 편차제곱의 평균이므로
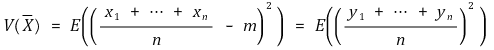
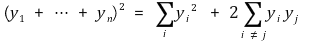
에서 b12, b22, ···, bN2은 각각 N-1Cn-1번씩 등장하고, b1b2, ···, bN-1bN은 각각 N-2Cn-2번씩 등장하므로
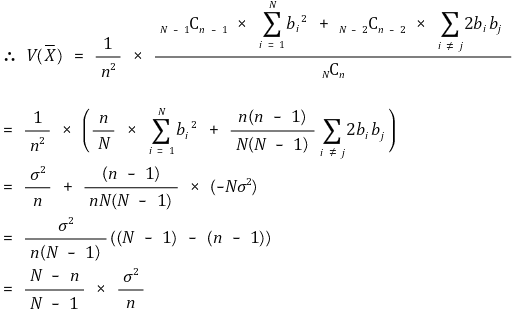
입력 : 2019.06.18 21:39
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 11강. 표본집단과 표본분포 (0) | 2019.06.19 |
|---|---|
| 【통계학】 8강. 확률변수변환 (0) | 2019.06.19 |
| 【통계학】 9강. 통계학 주요 정리 1부 (0) | 2019.06.18 |
| 【통계학】 7강. 연속확률분포 (1) | 2019.06.16 |
| 【통계학】 6강. 이산확률분포 (0) | 2019.06.16 |




최근댓글