3-2강. 몬티홀 문제(Monty hall problem)
추천글 : 【통계학】 3강. 확률공간
1. 상황 [본문]
2. 전제 [본문]
3. 정의 [본문]
4. 조건부 확률 [본문]
5. 베이즈 정리 [본문]
6. 결론 [본문]
1. 상황 [목차]

⑴ 세 개의 문 중 한 개의 문 뒤에 슈퍼카가 대기
⑵ 쇼 참가자는 세 개의 문 중 한 개의 문을 선택
⑶ 쇼 진행자는 쇼 참가자가 열지 않은 문 중 임의로 하나를 개방
⑷ 쇼 참가자는 기존의 선택을 고수하거나 선택을 바꿀 수 있음
⑸ 문제 : 어떤 선택이 합리적인가?
2. 전제 [목차]
⑴ 쇼 참가자는 최초에 1번 문을 선택
⑵ 쇼 진행자는 3번 문을 개방
3. 정의 [목차]
⑴ P(ⅰ) : 1번 문 뒤에 슈퍼카가 있을 확률
⑵ P(ⅱ) : 2번 문 뒤에 슈퍼카가 있을 확률
⑶ P(ⅲ) : 3번 문 뒤에 슈퍼카가 있을 확률
⑷ P(Ⅰ) : 쇼 진행자가 1번 문을 선택할 확률
⑸ P(Ⅱ) : 쇼 진행자가 2번 문을 선택할 확률
⑹ P(Ⅲ) : 쇼 진행자가 3번 문을 선택할 확률
⑺ P(ⅰ), P(ⅱ), P(ⅲ)는 사전확률(원인)
⑻ P(Ⅰ), P(Ⅱ), P(Ⅲ)는 사후확률(결과)
4. 조건부 확률 [목차]
⑴ P(ⅰ | Ⅲ) : 쇼 진행자가 3번 문을 선택했을 때, 1번 문 뒤에 슈퍼카가 있을 확률
⑵ P(Ⅲ | ⅰ) : 1번 문 뒤에 슈퍼카가 있을 때, 쇼 진행자가 3번 문을 선택할 확률
5. 베이즈 정리 [목차]
⑴ P(ⅰ | Ⅲ)
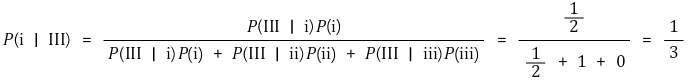
⑵ P(ⅱ | Ⅲ)
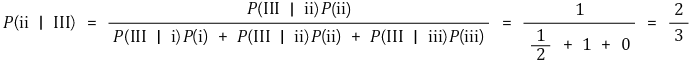
⑶ P(ⅲ | Ⅲ)
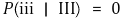
6. 결론 [목차]
⑴ 쇼 참가자는 최초의 선택을 바꾸는 게 유리함
입력: 2019.07.03 22:06
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 14-3강. Kruskal-Wallis H test (0) | 2019.08.24 |
|---|---|
| 【통계학】 14-1강. 통계적 검정 예시 총정리 (0) | 2019.07.24 |
| 【통계학】 3-1강. 포함배제의 원리 (0) | 2019.06.27 |
| 【통계학】 15강. 분산분석(ANOVA) (5) | 2019.06.21 |
| 【통계학】 14강. 통계적 검정 (0) | 2019.06.19 |




최근댓글