14-6강. Fisher Exact Test (Fisher 정확 검정, hypergeometric test)
추천글 : 【통계학】 14강. 통계적 검정
1. 예제 [본문]
2. 설명 [본문]
3. 응용 [본문]
a. 카이제곱검정 테스트
1. 예제 [목차]

⑴ 위와 같은 표를 contingency table이라고 함
2. 설명 [목차]
⑴ 전제 : marginal total이 알려져 있음
① marginal total : a + b, c + d, a + c, b + d를 지칭
② a + b + c + d = n이란 것도 알려져 있음
⑵ 귀무가설 H0 : 남성 집단과 여성 집단이 동일한 집단
⑶ 귀무가설 변형 : 남성 집단은 n 명 중 a + c 명을 무작위로 추출한 집단에 불과함
⑷ 통계량 1. 확률 (표본과 같이 나올 확률) : 무작위로 추출한 a + c 명 중 a 명이 공부 중일 확률

① 분모 : n 명 중 a + c 명을 무작위로 추출하는 경우
② 분자 : n 명 중 a + c명이 남자이고, a + b명은 공부 중이며 (전제), a명이 공부 중인 남자인 경우
③ 위 계산은 초기하분포(hypergeometric distribution)와 동일한 식을 보임
⑸ 통계량 2. 교차비(odds ratio) : 주어진 남성 집단, 여성 집단이 similar한지 dissimilar를 보여주는 척도
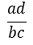
① - log (odds ratio)와 같이 나타내기도 함
② 유전자 집단 분석에서 fold change와 유사한 개념
③ 교차비가 1이면 두 집단이 매우 유사함을 의미함
⑹ 통계량 3. 비율(ratio) : 일반적으로 a / (a+c)를 나타냄
⑺ 통계량 4. 개수(count) : 보통 주어진 두 집합의 교집합 원소의 개수인 a를 나타냄
⑻ 통계량 5. p-value : 주어진 확률 p와 같거나 더 작은(= 더 극단적인) p 값이 나올 확률
⑼ 계산된 p value가 매우 작은 경우
① n명 중 남성 집단을 추출하는 행위는 무작위로 추출하는 행위가 아님
② 즉, 남성 집단과 여성 집단은 다른 집단
○ '다르다'는 것은 studying을 하는 행위에 있어서 남성과 여성의 비율이 유의하게 차이난다는 의미
3. 응용 [목차]
⑴ 샘플의 크기의 영향
① 샘플의 크기와 상관없이 사용 가능
② 일반적으로 샘플의 크기가 작을 때 사용
○ 샘플의 크기가 큰 경우 일반적으로 chi-squared test를 사용
○ 팩토리얼 계산값의 크기 때문에 Fisher exact test는 일반적으로 샘플의 크기가 작을 때 사용함
○ 다만 팩토리얼 계산값의 크기는 로그 계산으로 우회할 수 있음
③ 단, p value가 너무 작은 경우 Fisher exact test만 사용함
○ chi-squared test는 근사에 기반한 방법이므로 이 경우 항상 0을 출력하게 됨
⑵ 두 집합의 유사성 내지 동일성을 검정할 때도 사용할 수 있음

Figure. 2. Fisher's exact test를 이용한 두 집합의 유사성 검정
① Figure. 1.의 'Studying'이 Figure. 2.의 A 집합과 대응되고 'Men'이 B 집합과 대응
⑶ 일반적인 S × T 테이블에서의 확률값
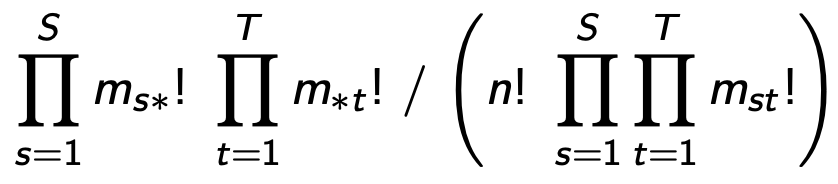
① M = (mst : s = 1, ···, S; t = 1, ···, T)
② row sum : (ms* : s = 1, ···, S)
③ col sum : (m*t : t = 1, ···, T)
④ n = ∑s∑t mst
⑷ R에서의 구현
my.Fisher.exact.test <- function(total, A, B, cross){
a1 <- log10_factorial(A)
a2 <- log10_factorial(total - A)
a3 <- log10_factorial(B)
a4 <- log10_factorial(total - B)
b1 <- log10_factorial(cross)
b2 <- log10_factorial(A - cross)
b3 <- log10_factorial(B - cross)
b4 <- log10_factorial(total - cross - (A - cross) - (B - cross))
b5 <- log10_factorial(total)
out = a1 + a2 + a3 + a4 - b1 - b2 - b3 - b4 - b5
return(10^out)
}
입력: 2019.08.24 01:28
수정: 2022.04.18 11:23
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 1-1강. 분위수 대 분위수 플롯(Q-Q plot) (0) | 2019.10.10 |
|---|---|
| 【통계학】 14-7강. 카이제곱검정 테스트 (3종류) (0) | 2019.10.05 |
| 【통계학】 14-3강. Kruskal-Wallis H test (0) | 2019.08.24 |
| 【통계학】 14-1강. 통계적 검정 예시 총정리 (0) | 2019.07.24 |
| 【통계학】 3-2강. 몬티홀 문제 (0) | 2019.07.03 |




최근댓글