20강. 회귀분석의 분산분석
추천글 : 【통계학】 통계학 목차
1. 단순선형회귀분석의 분산분석 [목차]
⑴ 문제 상황
| 나이 (년) | 진드기의 수 |
| 3 | 5 |
| 6 | 13 |
| 9 | 16 |
| 12 | 14 |
| 15 | 18 |
| 18 | 23 |
| 21 | 20 |
| 24 | 32 |
| 27 | 29 |
| 30 | 28 |
⑵ t 통계표
| 요인 | 계수 | 표준오차 | t | significance |
| 절편 | 5.733 | 2.265 | 2.531 | 0.035 |
| 나이 | 0.853 | 0.122 | 7.006 | 0.001 |
Table. 2. t 통계표

⑶ F 통계표
| 요인 | 제곱합 | df | 평균제곱 | F | significance |
| regression | 539.648 | 1 | 539.648 | 49.086 | < 0.001 |
| residual | 87.952 | 8 | 10.994 | ||
| 총합 | 627.600 | 9 |
Table. 3. F 통계표
① 귀무가설 H0 : 회귀선의 기울기가 0과 다름 없음
② 발상 : MS of Regression > MS of Residual이면 회귀선의 기울기는 0이 아님
③ 계산
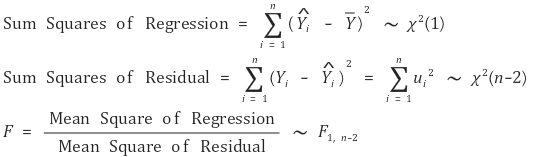
④ 회귀선의 자유도가 1인 이유 : 회귀변수가 한 개이므로
⑷ F 통계량이 t 통계량보다 검정력이 높은 이유 : F 통계량의 p value가 더 작음
① F 통계량은 t 통계량보다 더 많은 정보를 이용
② 마치 샘플 사이즈가 커지는 효과로 인해 F 통계량의 검정력이 더 큼
2. 공변량 분석(ANCOVA, analysis of covariance) [목차]
⑴ 개요
① one-way ANOVA에 단순선형회귀분석을 융합하는 개념
② 필요성 : 실제 문제 상황에서 한 요인의 교락효과로 제2의 요인이 달라지고, 이로 인해 종속변수에 영향을 미칠 수 있음
③ two-way ANOVA와의 차이점 : ANCOVA 기법은 특정 ANOVA 기법과 경합하지 않음. 두 기법을 동시에 할 수 있음
⑵ 문제상황
① 독립변수 : 오염된 광산 지역과 그렇지 않은 지역
② 종속변수 : 렛(rat)들의 장기의 납 농도
③ 교락효과(confounding effect) : 나이
⑶ 나이를 고려하지 않은 결과표
| 요인 | 제곱합 | 자유도 | 평균제곱 | F 비 |
| Treatment | SS Treatment | k-1 | MS treatment = SS Treatment / (k-1) | F = MS Treatment / MS Error |
| Error | SS Error | N-k | MS Error = SS Error / (N-k) | |
| 합계 | SS Total | N-1 |
Table. 4. 단순한 one-way ANOVA 결과표
① 나이 효과가 통제되지 않으면 잔차가 더 커짐
② 잔차가 커지면 MS Error가 커지고 F 비가 작아짐
③ F 비가 작아지면 검정력이 떨어짐 : 즉, treatment의 유의성 입증이 어려움
⑷ 가정
① 등분산성(homoscedasticity)
② 독립성(independency)
③ 정규성(normality)
④ 공변량(covariate)과 종속변수의 관계가 선형일 것
⑤ 평행성(parallelism)
○ 예를 들면 오염된 광산 지역과 그렇지 않은 지역 각각의 회귀선을 계산 시 기울기가 같을 것
○ 평행성을 만족한다는 것은 상호작용이 없다는 것과 동일한 의미
○ 만일 평행성이 만족하지 않으면 하나의 선택된 값(예 : 나이의 전체 평균)에 대해 차이를 비교하는 것은 공변량의 범위 전체를 대표할 수 없음
Figure. 1. ANCOVA에서 평행성이 결여된 예
○ ANCOVA를 하기 전에 나이와 지역의 상호작용을 먼저 평가하여 평행성을 확인해야 함
⑸ 과정
① 1st. 나이와 납의 상관관계 확인
② 2nd. 나이와 지역의 상호작용(interaction)이 통계적으로 유의하지 않음을 확인
| 요인 | 제곱합 | 자유도 | 평균제곱 | F 비 | p value |
| Age | |||||
| Site | |||||
| Age × Site | NS | ||||
| Error | |||||
| Total |
Table. 5. 상호작용을 포함한 결과표
③ 3rd. 납에 대한 나이의 회귀선 계산
④ 4th. 3rd에서 얻은 회귀선으로부터 다음 조건을 만족하는 두 개의 회귀선을 계산
○ 3rd에서 얻은 회귀선의 기울기는 유지한 채 y절편만 변경
○ 각 독립변수의 level에 대해서 제곱합이 최소가 되도록 할 것
⑤ 5th. 4th에서 얻은 각 회귀선으로부터 잔차 계산
⑥ 6th. 전체 집단에 대한 나이의 평균을 구한 뒤 그 값에 대한 각 회귀선의 함수값을 표준값으로 지정
○ 전체 집단에 대한 나이의 평균은 한 예시일 뿐 어떤 값이든 상관 없음
⑦ 7th. 각 treatment 그룹에 대해 표준값에서 5th에서 구한 잔차를 위아래로 표시
⑧ 8th. 최종적으로 SS Error가 더 작아졌음을 확인할 수 있음 : p value가 더 작아짐
⑹ 결과
① 보정 결과
② 보정 전 결과표
| 요인 | 제곱합 | 자유도 | 평균제곱 | F 비 | p value |
| Site | 320 | 1 | 320 | 2.74 | 0.115 |
| Error | 2100.8 | 18 | 116.71 | ||
| Total | 2420.800 | 19 |
Table. 6. 보정 전 결과표
③ 보정 후 결과표 : 회귀선으로부터 Age에 대한 제곱합을 계산할 수 있음
| 요인 | 제곱합 | 자유도 | 평균제곱 | F 비 | p value |
| Age | 1776.290 | 1 | 1776.290 | 93.054 | < 0.001 |
| Site | 1094.335 | 1 | 1094.335 | 57.329 | < 0.001 |
| Error | 324.510 | 17 | 19.089 | ||
| Total | 2420.800 | 19 |
Table. 7. 보정 후 결과표
④ 보고 양식 : A preliminary analysis for parallelism showed no significant difference between the slopes of the lines for lead concentration in relation to age (age × site: F1,16 = 0.00, NS). The subsequent ANCOVA showed a significant effect of site (F1,17 = 57.329, P < 0.001) as well as a significant effect of the covariate (age) (F1,17 = 93.054, P < 0.001). Rats from the mine site had higher levels of lead than those from the control.
⑺ 오염된 광산 지역의 회귀선과 그렇지 않은 지역의 회귀선의 y 절편을 비교하지 않는 이유
① 상황 : 평행성(parallelism)을 만족하는 경우 y 절편을 비교하는 것이 훨씬 쉬움
② y 절편의 비교는 샘플 사이즈가 한 표본집단의 샘플 사이즈 수준
③ ANCOVA는 전체 에러 텀을 가지고 계산하므로 샘플 사이즈가 한 표본집단의 샘플 사이즈의 두 배 수준
④ 따라서 ANCOVA를 하면 y 절편을 단순 비교하는 것보다 검정력이 높아짐
⑻ 응용 1. 2-factor ANCOVA
① 2-factor ANOVA 분석 시 ANCOVA 기법을 적용하는 것
② 예 : 독립변수가 성별, 약물이고 종속변수가 혈압이고 교락요인이 나이인 경우
⑼ 응용 2. 교락요인이 여러 개인 경우
① 다중선형회귀분석을 이용
② 고급 회귀이론을 사용할 수도 있음
입력: 2019.12.07 23:04
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 5-1강. 이미지 유사성 비교 : SSIM (2) | 2021.02.19 |
|---|---|
| 【통계학】 전하는 말 (0) | 2020.03.24 |
| 【통계학】 통계학 요점 정리 (0) | 2019.12.07 |
| 【통계학】 19강. 고급 회귀분석 (0) | 2019.11.26 |
| 【통계학】 16강. 선형 회귀분석 (0) | 2019.11.24 |














최근댓글