5-2강. 거리함수와 유사도
추천글 : 【통계학】 5강. 통계량
1. 개요 [본문]
2. 노음 개념 종류 [본문]
3. 거리 개념 종류 [본문]
4. 유사도 개념 종류 [본문]
a. Gromov-Wasserstein distance
※ 일부 거리 개념과 유사도 개념이 잘못 분류됐을 수도 있습니다.
1. 개요 [목차]
⑴ 노음과 거리의 차이 : 많이 혼용되어 쓰임
① 노음(노름, norm)

② 거리함수(distance function, metric)

③ 노음이 정의되면 거리(distance) d를 정의할 수 있음

④ 거리가 정의돼 있다고 하여 대응되는 노음이 항상 존재하는 것은 아님
⑵ 거리와 유사도의 차이 : 많이 혼용되어 쓰임
① 공통점 : 두 data point가 가깝다(거리가 짧다)는 말은 유사하다는 뜻과 동일함. 즉, 거리 ∝ 1 / 유사도
② 공통점 : 머신러닝에서의 손실함수, 에러함수, 비용함수라는 말도 참값과 예측값의 차이(∝ 1 / 유사도)를 지칭함
③ 차이점 : 거리함수는 선형대수학에서 다음과 같이 엄밀하게 정의되지만, 손실함수, 유사도 등이 그 정의를 만족해야 하는 것은 아님
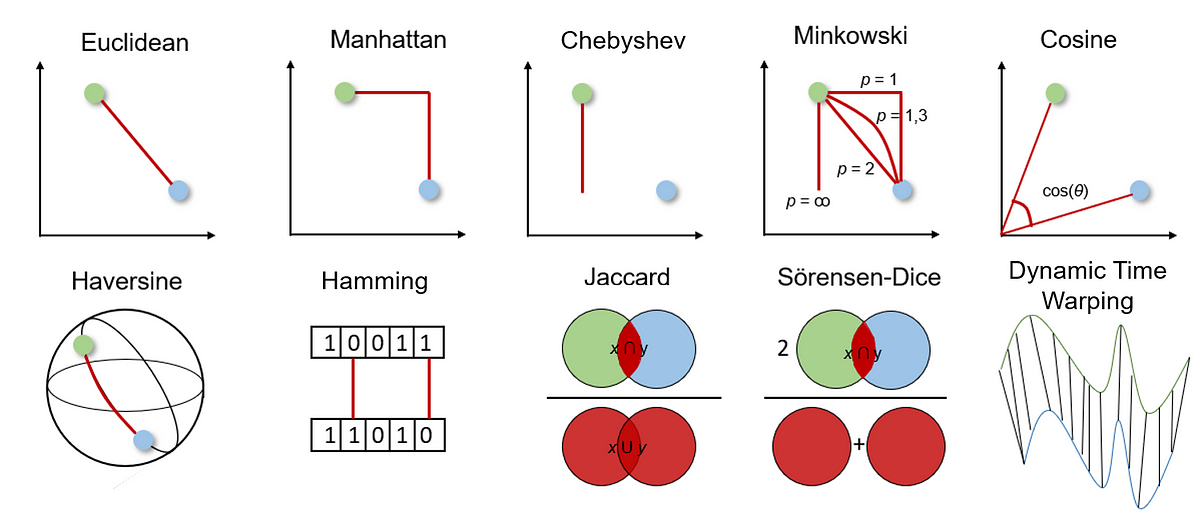
⑶ 여러 종류의 거리, 유사도 개념
Figure. 1. 여러 종류의 거리, 유사도 개념
2. 노음 개념 종류 [목차]
⑴ 종류 1. L1 노음(L1 노름, L1-norm)
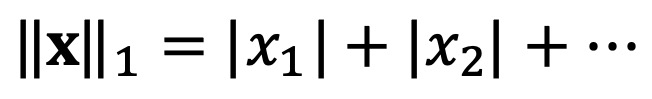
⑵ 종류 2. L2 노음(L2 노름, L2-norm)
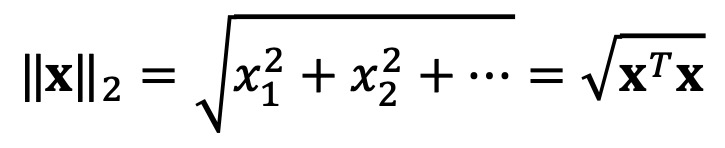
⑶ 종류 3. p 노음(p 노름, p-norm) : p가 ∞인 경우를 d∞ norm이라고 함
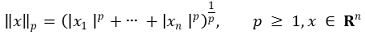
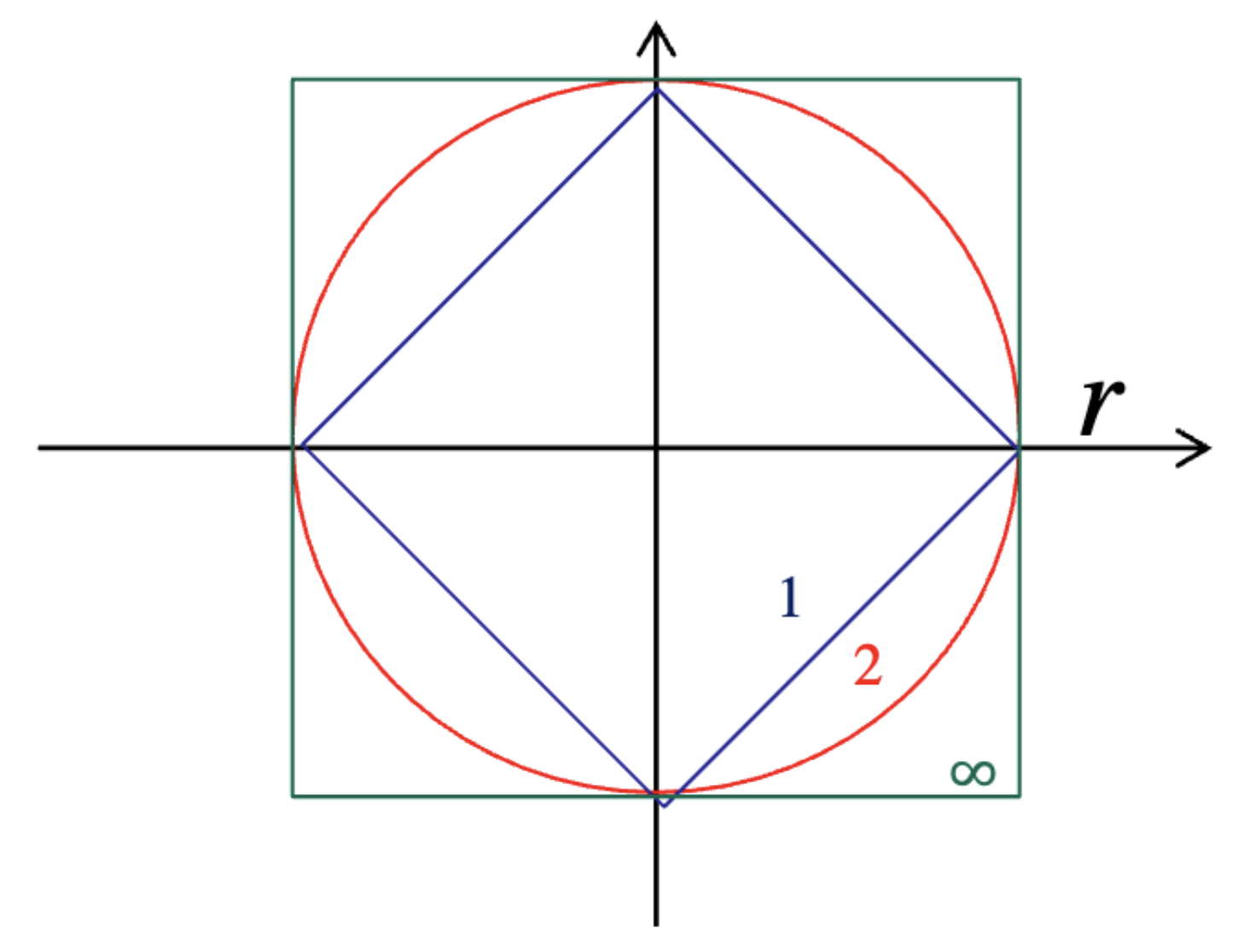
Figure. 2. p 값에 따른 p-norm = 1인 구간의 경향성
⑷ 종류 4. Frobenius norm
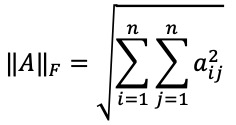
3. 거리 개념 종류 [목차]
⑴ 종류 1. L1 손실함수(L1 거리, 시가 거리, MAE, city-block distance, taxicab distance, rectilinear distance, Manhattan distance, sparse learning, compressed sensing)
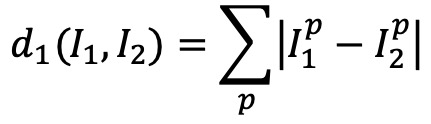
① 즉, ㄱ, ㄴ 자 모양 등으로 경로를 설정한 뒤 각 거리를 구하는 방식
② MAPE는 다음과 같이 비슷하게 정의됨

⑵ 종류 2. L2 손실함수(L2 거리, MSE) : 피타고라스 정리를 이용한 유클리드 거리 (표준)
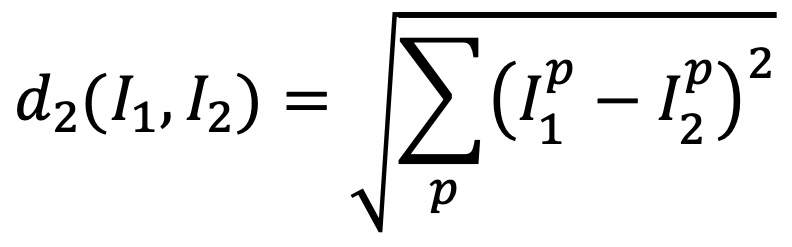
① PSNR(peak signal to noise ratio) : MSE를 데시벨로 나타낸 것
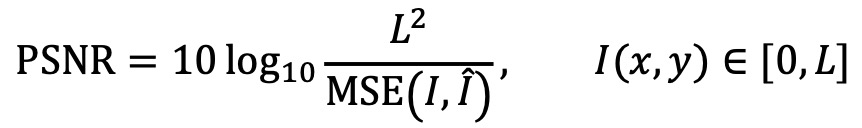
⑶ 종류 3. maximum metric (Chebyshev distance supremum distance, uniform distance, chessboard distance, d∞ distance)
① p = ∞인 p-norm으로 정의한 || x - y ||∞ : 체스말 중 킹을 연상
② 거리 계산 시 dominant dimension (feature)를 보고 나머지는 무시
③ 응용 : 신호처리이론의 sample entropy, 제어이론에서 robust control
⑷ 종류 4. cross entropy : 대표적으로 BCE(binary cross-entropy)가 있음
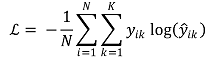
⑸ 종류 5. 정보이론에서의 거리
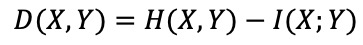
⑹ 종류 6. DT(Delaunay triangulation)
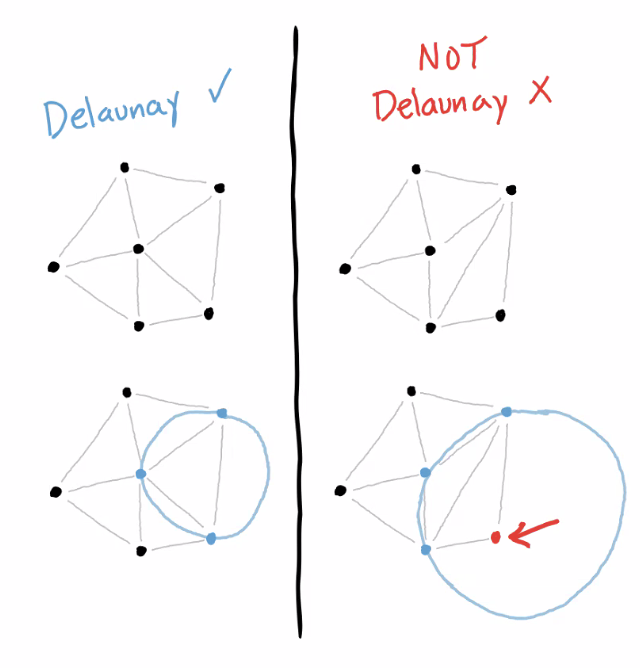
Figure. 3. Delaunay triangulation 예시
⑺ 종류 7. 벡터 연산
① 7-1. dot product : 벡터의 내적
② 7-2. Hadamard product : element-wise multiplication
⑻ 종류 8. linkage metric : 클러스터 간 거리를 정의
⑼ 종류 9. 헤밍 거리(Hamming (edit) distance)
① 데이터 포인트마다 이진값을 지정해 값의 차이만큼을 데이터 포인트의 거리로 측정. 정보 이론에서 많이 사용
② 두 string은 길이가 같아야 함
③ 예 : (0, 1, 1, 0, 0, 1)와 (1, 1, 1, 1, 0, 0)은 1, 4, 6번째 값이 달라서 헤밍 거리는 3
⑽ 종류 10. 표준화(standardized distance)
① 변수의 측정단위를 표준화한 거리
② 수식화
d(i, j)2 = (Xi - Xj)T D-1 (Xi - Xj)
○ Xi : 시작점 행렬
○ Xj : 끝점 행렬
○ D : 표본 분산 (대각) 행렬
⑾ 종류 11. 마할라노비스 거리(Mahalanobis distance)
Figure. 4. 마할라노비스 거리
이 그림에서 X 벡터는 일반적인 열벡터가 아닌 행벡터로 주어져 있음을 유의
① 변수의 표준화와 함께 변수 간의 상관성(데이터의 분포 형태)을 동시에 고려한 통계적 거리
② 수식화 : 두 데이터 포인트 Xi와 Xj 간의 거리 d를 구하고자 할 때 다음과 같은 수식을 사용함
d(i, j)2 = (Xi - Xj)T S-1 (Xi - Xj)
○ Xi : 시작점 행렬
○ Xj : 끝점 행렬
○ S : 표본 공분산 행렬
○ S는 양반정부호 행렬(positive semi-definite matrix) : (Xi - Xj)tS-1(Xi-Xj) ≥ 0이 성립하기 때문
○ 데이터에 종속적인 변수들이 포함돼 있거나 데이터가 차원에 비해 적은 수의 표본을 가질 경우 S = 0일 수 있음
③ 장점 : 유클리드 거리와 달리 scale-free, 데이터의 분포 및 상관성 고려, outlier 탐지 등의 이점이 있음
○ 유클리드 거리가 spherical distance라면 마할라노비스 거리는 elliptical distance
④ 한계 : 데이터의 normality를 가정해야 함. 표본 공분산 행렬을 구하는 과정이 computatinoally intensive
⑤ 파이썬 코드
import numpy as np
from scipy.linalg import inv
def mahalanobis_distance(x, y, covariance_matrix, regularization=1e-6):
# Add regularization to the covariance matrix's diagonal
regularized_cov = covariance_matrix + np.eye(covariance_matrix.shape[0]) * regularization
x_minus_y = np.array(x) - np.array(y)
covariance_matrix_inv = inv(regularized_cov)
distance = np.dot(np.dot(x_minus_y, covariance_matrix_inv), x_minus_y.T)
return np.sqrt(distance)
# Example usage:
x = [1, 2, 3]
y = [4, 5, 6]
data = np.array([x, y])
cov_matrix = np.cov(data, rowvar=False) # Here, we're just using the covariance of x and y for simplicity
print(mahalanobis_distance(x, y, cov_matrix))
⑿ 종류 12. Levenshtein (edit) distance
① 두 개의 문자열 A, B가 주어졌을 때 두 문자열이 얼마나 유사한지를 알아내는 알고리즘
○ 구체적으로는, 어떤 시퀀스를 다른 시퀀스로 바꾸기 위해 필요한 치환, 삽입 또는 삭제의 횟수
○ 문자열의 길이가 다를 수 있으므로, Levenshtein 거리의 하한은 문자열 길이 차이가 됨
② 수식화
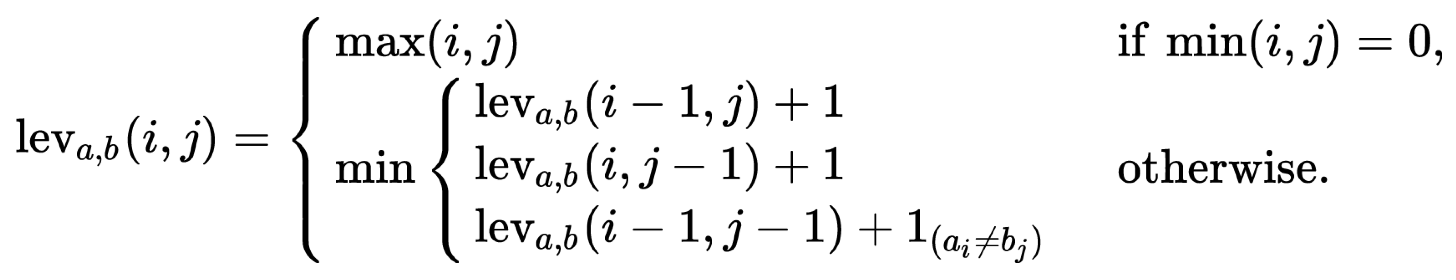
○ i, j는 각각 string a, b를 위한 반복 변수
○ 1(a≠b) : a = b이면 0, a ≠ b이면 1
⒀ 종류 13. 민코프스키(Minkowskii) 거리
① m차원 민코프스키 공간에서의 거리
② m = 1일 때 맨하탄 거리와 같음
③ m = 2일 때 유클리드 거리와 같음
⒁ 종류 14. Hausdorff distance
① 수식화 : 두 집합 A = {a1, ∙∙∙, ap}, B = {b1, ∙∙∙, bq}에 대하여
H(A, B) = max(h(A, B), h(B, A))
② directed Hausdorff distance : A, B 중 가장 거리가 먼 두 점의 거리
h(A, B) = maxa∈A minb∈B || a - b ||
⒂ 종류 15. focal loss
① 수식화
FL = -(1 - Pt)γ log (Pt)
⒃ 종류 16. Sørensen–Dice coefficient (Dice distance, DSC)
① 수식화
2 | A ∩ B | / | A ∪ B |
⒄ 종류 17. Gromov-Wasserstein distance (Kantorovich–Rubinstein metric, Earth Mover's Distance, EMD)
⒅ 종류 18. Jensen-Shannon distance

⒆ 종류 19. total variation (TV) distance
⒇ 종류 20. Kolmogorov-Sminrov distance
⒇ 종류 21. Hellinger distance : 확률밀도함수의 kernel density estimation을 요함
⒇ 종류 22. Huber loss function
⒇ 종류 23. Bhattacharyya loss
⒇ 종류 24. ELBO (evidence lower bound)
⒇ 종류 25. Aitchison distance : simplex의 거리 개념
⒇ 종류 26. Bray Curtis distance
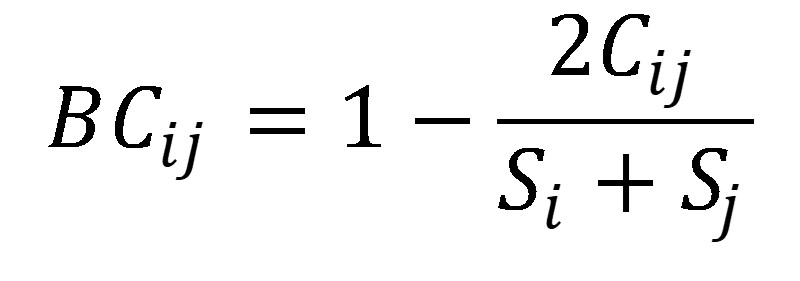
① i = one site, j = another site
② Si = numbers of species in i, Sj = numbers of species in j
③ Cij = the less number of the overlapping sites in species
⒇ 종류 27. Fourier loss
⒇ 종류 28. Cook's distance : 생물정보학에서 outlier를 식별할 때 사용
⒇ 종류 29. Fisher-Rao distance
4. 유사도 개념 종류 [목차]
⑴ 종류 1. 피어슨 상관계수(Pearson correlation coefficient)
① 정의 : X와 Y의 표준편차 σx, σy에 대해,
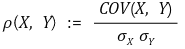
② 특징
○ 등간, 비율척도로 측정된 두 변수들의 상관관계
○ 연속형 변수를 대상으로 함
○ 정규성 가정
○ 대부분 많이 사용
⑵ 종류 2. Spearman 상관계수(Spearman correlation coefficient)
① x' = rank(x)와 y' = rank(x)에 대해 다음과 같이 정의
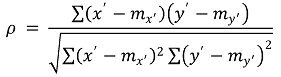
② 특징
○ 서열 척도인 두 변수들의 상관관계를 측정하는 방식
○ 순서형 변수를 대상으로 하는 비모수적 방법
○ 제로가 많은 데이터에 유리함
○ 데이터 내 편차나 에러에 민감
○ 켄달 상관계수보다 높은 값을 가짐
⑶ 종류 3. Kendall 상관계수(Kendall correlation coefficient)
① concordant pair와 discordant pair에 대해 상관계수를 정의
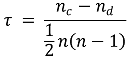
② 특징
○ 열 척도인 두 변수들의 상관관계를 측정하는 방식
○ 순서형 변수를 대상으로 하는 비모수적 방법
○ 제로가 많은 데이터에 유리함
○ 샘플 사이즈가 작거나 데이터의 동률이 많을 때 유용함
⑷ 종류 4. Matthew correlation coefficient (MCC)

⑸ 종류 5. χ2
① 측정데이터를 xm, ym, 근사함수를 f(x)라 하면,

⑹ 종류 6. 에너지 통계량
① 2007년 Székely, Rizzo, Bakirov이 제안
② 거리 공분산(distance covariance) V(X,Y)과 거리 상관계수(distance correlation) V(X,Y) / √V((X,X)·V(Y,Y))

⑺ 종류 7. SSIM
① 이미지 유사도 비교 알고리즘
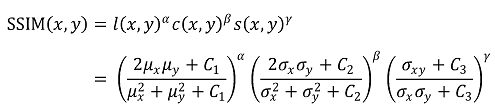
② 파이썬 코드
## Method 1
def SSIM(x, y):
# assumption : x and y are grayscale images with the same dimension
import numpy as np
def mean(img):
return np.mean(img)
def sigma(img):
return np.std(img)
def cov(img1, img2):
img1_ = np.array(img1[:,:], dtype=np.float64)
img2_ = np.array(img2[:,:], dtype=np.float64)
return np.mean(img1_ * img2_) - mean(img1) * mean(img2)
K1 = 0.01
K2 = 0.03
L = 256 # when each pixel spans 0 to 255
C1 = K1 * K1 * L * L
C2 = K2 * K2 * L * L
C3 = C2 / 2
l = (2 * mean(x) * mean(y) + C1) / (mean(x)**2 + mean(y)**2 + C1)
c = (2 * sigma(x) * sigma(y) + C2) / (sigma(x)**2 + sigma(y)**2 + C2)
s = (cov(x, y) + C3) / (sigma(x) * sigma(y) + C3)
return l * c * s
## Method 2
from skimage.metrics import structural_similarity as ssim
import cv2
x = cv2.imread('x.png', cv2.IMREAD_GRAYSCALE)
y = cv2.imread('y.png', cv2.IMREAD_GRAYSCALE)
score, diff = ssim(x, y, full=True)
print("SSIM:", score)
⑻ 종류 8. mutual information
① 원리 : 첫 번째 이미지가 주어졌을 때 두 번째 이미지를 예측할 수 있는지
② 서로 다른 모달리티로 얻어진 두 이미지 간의 연관성을 분석할 때 용이함
○ 예 : MRI에서 T1-weighted image와 T2-weighted image는 반전된 지점이 많은데, mutual information은 이를 고려할 수 있음
③ 코드
def mutual_information(img1, img2):
import numpy as np
import cv2
import matplotlib.pyplot as plt
# img1 and img2 are 3-channel color images
a = img1[:,:,0:1].reshape(img1.shape[0], img1.shape[1])
b = img2[:,:,0:1].reshape(img2.shape[0], img2.shape[1])
hgram, x_edges, y_edges = np.histogram2d(
a.ravel(),
b.ravel(),
bins=20
)
pxy = hgram / float(np.sum(hgram))
px = np.sum(pxy, axis=1) # marginal for x over y
py = np.sum(pxy, axis=0) # marginal for y over x
px_py = px[:, None] * py[None, :] # Broadcast to multiply marginals
nzs = pxy > 0 # Only non-zero pxy values contribute to the sum
return np.sum(pxy[nzs] * np.log(pxy[nzs] / px_py[nzs]))
④ 레퍼런스
Mutual information as an image matching metric — Tutorials on imaging, computing and mathematics
\(\newcommand{L}[1]{\| #1 \|}\newcommand{VL}[1]{\L{ \vec{#1} }}\newcommand{R}[1]{\operatorname{Re}\,(#1)}\newcommand{I}[1]{\operatorname{Im}\, (#1)}\) Mutual information as an image matching metric In which we look at the mutual information measure for com
matthew-brett.github.io
⑼ 종류 9. 상대 엔트로피(relative entropy, Kullback-Leibler divergence, KL divergence, KLD)

⑽ 종류 10. Sinkhorn divergence (entropic Wasserstein distance)
⑾ 종류 11. Cressie-Read power divergence
⑿ 종류 12. Mr(thresholded Mander's colocalization coefficient)
① 서로 다른 두 개의 단색 이미지의 overlapping pixel의 비율
② tMr(thresholded Mr) : 특정 threshold 이하의 값을 모두 0의 값을 갖는 backgroun로 간주하고 Mr을 구한 것
③ 배경 : Pearson correlation coefficient는 음수 값을 가지고 있어서 단색 이미지 간 비교에 적절하지 않음
④ 특징 1. 0 ~ 1 사이의 값을 가짐
⑤ 특징 2. 배경의 픽셀값에는 민감하게 변하지만 overlapping pixel의 값에는 크게 영향을 받지 않음
⑥ 특징 3. Pearson correlation에 의존성이 있음
⑦ 과정 1. 먼저 Pearson correlation을 통해 p-value를 얻어 colocalization있는지를 검정
⑧ 과정 2. colocalization이 있다면 tM1, tM2 값을 계산
⑨ 사용법 : ImageJ
⒀ 종류 13. 자카드 유사도(Jaccard similarity, IoU, intersection over union)
① 자카드 스코어 : 두 집합 A, B에 대하여,
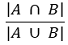
② 0과 1사이의 값을 가짐 : 두 집합이 동일하면 1의 값, 공통의 원소가 하나도 없으면 0의 값을 가짐
③ 명목형 변수 거리에 사용되는 방법
⒁ 종류 14. 코사인 유사도(cosine similarity)
① 코사인 값 : 두 벡터 A, B에 대하여,
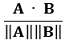
⒂ 종류 15. coverage score
① 두 집합 A, B에 대하여,
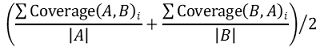
⒃ 종류 16. Fisher 정확 검정(Fisher exact test)
① 두 집합 A, B에 대하여,

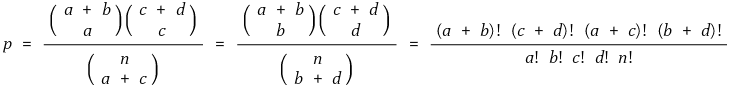
⒄ 종류 17. Faiss : 2023년 Meta에서 개발한 유사도 평가 함수
⒅ 종류 18. Smith–Waterman similarity : 핵산 혹은 아미노산 서열 간 유사성 평가 시 사용
⒆ 종류 19. MIC(maximum information coefficient)
⒇ 종류 20. 스펙트럼 유사도(spectral similarity) : 행렬 A, B를 비교할 때 고유벡터를 비교함. Laplacian 행렬과 그래프 이론과 관련
⒇ 종류 20. SCC(stratum-adjusted correlation coefficient) : stratum에 따른 가중치를 고려한 피어슨 상관계수
입력: 2022.08.02 16:03
수정: 2023.08.23 14:28
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 14-4강. 우도비 검정과 Wilks’ phenomenon 증명 (3) | 2024.09.25 |
|---|---|
| 【통계학】 Optimal Transport 및 Gromov-Wasserstein 거리 이해하기 (3) | 2023.11.04 |
| 【통계학】 14-5강. 런 검정(run test) (0) | 2023.09.22 |
| 【통계학】 17강. 비선형 회귀분석 (2) | 2021.12.11 |
| 【통계학】 14-8강. 윌콕슨 순위 검정(Wilcoxon Rank Test) (3) | 2021.05.10 |





최근댓글