1강. 신호처리(signal processing)
추천글 : 【신호처리】 신호처리이론 목차
1. 개요 [본문]
2. 변환 [본문]
3. Nyquist theorem [본문]
4. 필터 [본문]
1. 개요 [목차]
⑴ 정의
① 신호(signal) : t1, ..., tn (예 : 시간)이 주어졌을 때 수열 {x(tn)}을 지칭함
② 신호 처리(signal processing) : 신호로부터 정보를 추출하는 것
③ 신호 전처리 : 초기 데이터(raw data)에서 노이즈나 trend 성분을 제거하여 깨끗한 신호를 정제하는 것
⑵ 신호의 종류
① 종류 1. 연속 신호(continuous signal) : t가 연속이고, x가 연속인 신호
○ 저장(storage), 획득(acquisition), 처리(processing)이 극히 어려움
○ 예 : π라는 무리수 값을 저장, 획득, 처리하려면 무한 용량과 무한 시간이 필요함
② 종류 2. 이산 신호(discrete signal) : t가 이산이고. x는 연속인 신호
③ 종류 3. 디지털 신호(digital signal) : t가 이산이고, x가 이산인 신호
④ 샘플링(sampling, digitization) : 연속 신호를 이산 신호로 변환하는 것
⑤ (참고) Nyquist theorem : sampling rate가 시그널 주파수의 2배 이상이면 aliasing error 없이 샘플링 할 수 있다는 것
⑶ 신호는 2 이상의 차원을 가질 수 있음
① 2차원 신호 : t의 차원이 2인 신호를 이미지(image)라고 정의함
② 3차원 신호 : 예를 들어, coronary angiogram이 있음
③ 4차원 신호 : 예를 들어, radiotherapy in cancer가 있음
⑷ 시간이라는 도메인은 무한 개의 서로 다른 방법으로 변환할 수 있음 (예 : 푸리에 변환, 시간을 요일로 변환)
2. 변환 [목차]
⑴ 개요 : 신호를 변환하는 방법은 무한히 많음
⑵ 푸리에 변환(Fourier transformation)
① 정의 : 시간 도메인 신호에서 주파수 정보를 얻는 대표적인 방법
② 시간 도메인에서의 신호 x(t)가 주어졌을 때, 푸리에 변환을 통해 변환된 주파수 도메인 신호 X(f)는 다음과 같은 관계를 가짐
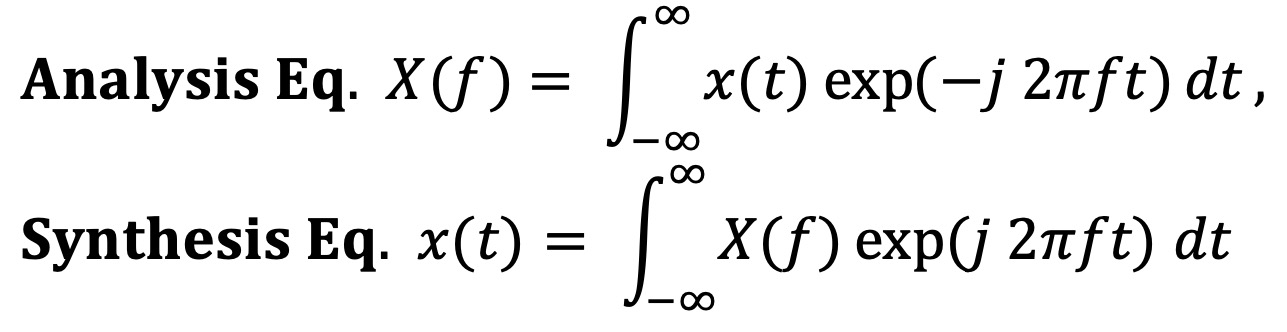
○ 표기 : X(f) = F{x(t)}
○ 푸리에 변환은 라플라스 변환의 특수한 경우
③ 푸리에 변환의 성질
○ 성질 1. 선형성(linearity) : F{ax1(t) + bx2(t)} = aF{x1(t)} + bF{x2(t)} = aX1(f) + bX2(f)
○ 참고로, 선형성 = 비례성(proportionality) + 중첩성(superposition)
○ 모든 시스템은 기본적으로 비선형적이지만, 미소 구간에서는 준선형성을 만족함
○ 성질 2. scaling : F{x(at)} = (1/a) × X(f/a). 불확정성 원리(uncertainty principle)와 관련 있음
○ 성질 3. shifting : F{x(t - a)} = X(f) exp(-j 2πaf)
○ ∴ |F{x(t - a)}| = |X(f)|
○ phase의 의미 : 신호가 언제 시작했는지를 알려주는데, 해석하기 어려워 위 성질에 기반해 보통 크기만 봄
○ 성질 4. convolution
○ x1(t) ⨂ x2(t) = ∫ x1(t) x2(t - τ) dτ = ∫ x1(t - τ) x2(τ) dτ라 정의하면,
○ F{x1(t) ⨂ x2(t)} = F{x1(t)} · F{x2(t)} = X1(f) · X2(f)
○ 성질 5. x(t)가 real function이라면, F{x(-t)} = X*(f)가 성립 (단, X*는 X의 켤레 복소수)
④ 주요 함수들의 푸리에 변환
| time function | frequency function |
| exp(-t), t ≥ 0 | 1 / (1 + j 2πf) |
| exp(-ax2) | √(π / a) · exp(-π2 k2 / a) |
| δ(t) (Dirac 함수) | 1 |
| dx(t) / dt | (j 2πf) X(f) |
| x(t - t0) | exp(-j 2πf t0) X(f) |
| exp(j 2πf0t) x(t) | X(f - f0) |
| x1(t) ⨂ x2(t) | X1(f) · X2(f) |
| x1(t) · x2(t) | X1(f) ⨂ X2(f) |
| tx(t) | (j / 2π) · (dX(f) / df) |
| ∫ |x(t)|2 dt (에너지) | ∫ |X(f)|2 df (에너지) |
Table. 1. 주요 함수들의 푸리에 변환
○ 가우시안 신호의 푸리에 변환은 다시 가우시안 : 이렇게 함수 개형이 유지되는 신호는 무한히 많음
⑤ 2차원 푸리에 변환 : 이미지 처리, tomography 등에서 응용
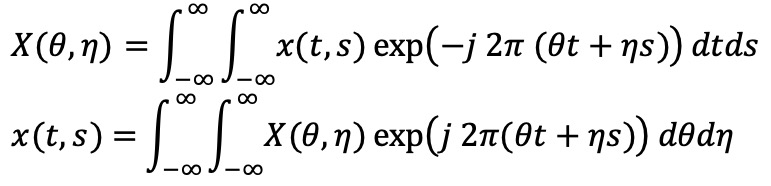
⑥ 연속 푸리에 변환(continuous Fourier transform; CFT)
○ 종류 : 압전기(piezoelectricity), 초음파 분석 (cf. Fresnel 산란과 Fraunhofer 산란)
⑦ 이산 푸리에 변환(discrete Fourier transform; DFT)
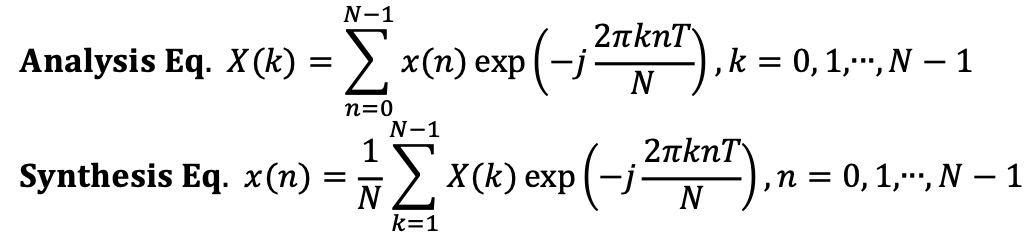
○ FFT(fast Fourier transform) : DFT를 여러 개로 나누어 각각 푸리에 변환을 하여 DFT를 효율적으로 계산하는 기법
⑧ 단점
○ 계산량이 많고, 기본 주파수 f 값을 설정하는 것에 주의가 필요함
○ 각 주파수의 신호들의 선후 관계를 주파수-세기 곡선에서 알 수 없음
○ 이유 : 푸리에 변환은 영원한 주기함수 신호를 가정으로 하지, 국소적인 신호가 입력되지 않을 것을 전제하기 때문
○ 단, 복잡한 위상 분석을 하면 선후 관계를 알 수 있음
⑨ 응용
○ 교류회로이론
○ 제어이론
○ 비침습 검사 : tomography, 분광학 등
○ 단백질 모델링
○ 스피치 인식 및 음향 인식
○ 미시 경제 분석
○ Fourier descriptor : 이미지를 복소수로 표현 후 푸리에 변환. object detection, smoothing, feature extraction 등을 수행함
⑶ 웨이브릿 변환(wavelet transformation)
① 배경 : 전통적인 푸리에 변환의 단점을 보완하기 위한 목적으로 만들어짐
② 원리 : 몇 개의 샘플링 주파수와 내적함으로써 해당 주파수와 유사 주파수의 신호를 분리
③ 종류 1. STFT(short-term Fourier transform) : 일반적인 웨이브릿 변환의 이전 단계
○ 정의 : 슬라이딩 윈도우 방식. 게이트 g, g의 복소수 g*에 대하여
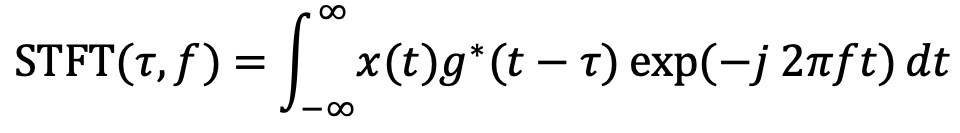
○ 장점 : 신호를 시간, 주파수 모두에 대해 얻을 수 있음
○ 단점 : g의 형태와 길이를 잘못 설정하면 효과가 없거나 신호 왜곡을 유발할 수 있음
② 종류 2. 연속 웨이브릿 변환(continuous wavelet transfer; CWT)
○ 수식화
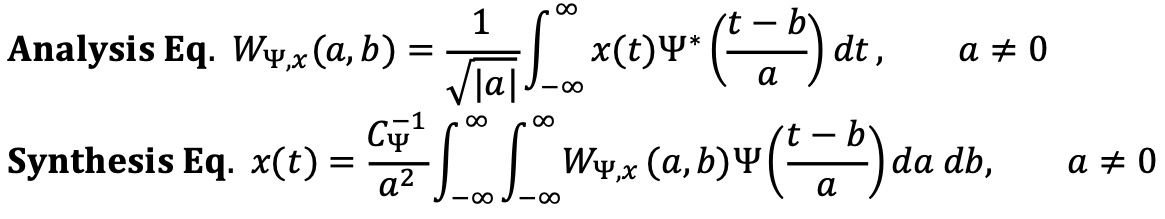
○ Ψ : mother wavelet (mother basis function)
○ Ψ* : Ψ의 복소수
○ b : shifting parameter
○ a : scaling (resolution) parameter
○ CΨ-1 : 상수
○ (참고) 시간 도메인 : 시간에 대한 높은 정확도, 주파수에 대한 낮은 (혹은 아예 없는) 정확도
○ (참고) 주파수 도메인 : 시간에 대한 낮은 (혹은 아예 없는) 정확도, 주파수에 대한 높은 정확도
○ 웨이브릿 도메인 : 시간에 대한 다중 해상도 정확도, 주파수에 대한 다중 해상도 정확도
○ mother wavelet의 종류 : 웨이브릿 변환 시 주어진 신호와 가장 닮은 mother wavelet을 골라야 함
○ Daubecies (dbX)
○ Harr
○ Mexican hat (sombrero)
○ Coiflets
○ Symlets
○ Morlet
○ Meyer
③ 종류 3. 이산 웨이브릿 변환(discrete wavelet transfer; DWT)
○ 개요
○ CWT와 상당히 다르게 분석을 수행함
○ Mallat pyramidal algorithm 혹은 QMF(quadrature mirror filter)를 사용
○ 장점 : 푸리에 변환에 비해 계산량이 적어 상당히 컴퓨팅 시간이 빠름
○ 원리
○ 의사 결정 트리처럼 신호를 high, low로 세분화 : 이때 high pass 필터와 low pass 필터를 사용
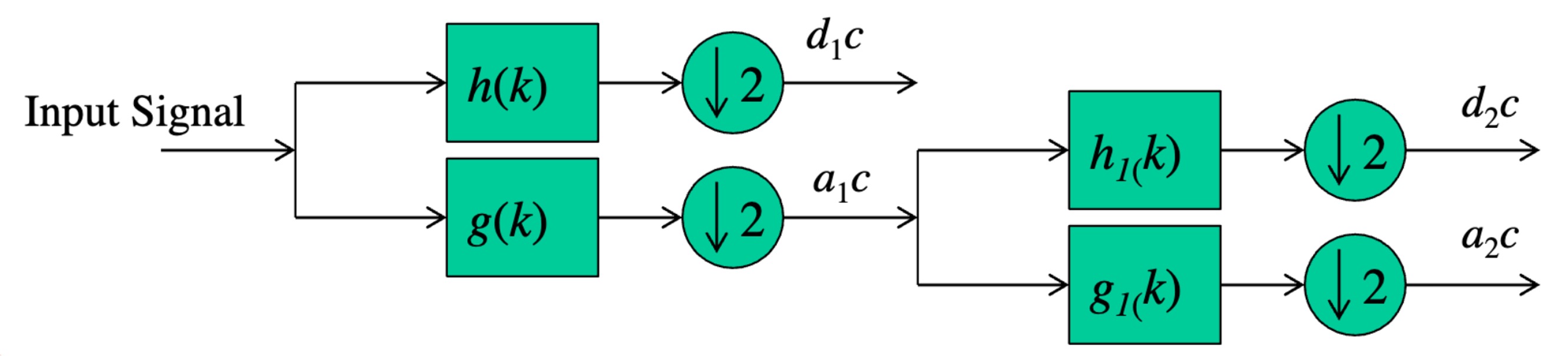
Figure. 1. DWT의 원리
○ 웨이브릿 함수 및 각 필터 함수 설계 : 기본 필터 함수 h로 설계할 수 있음
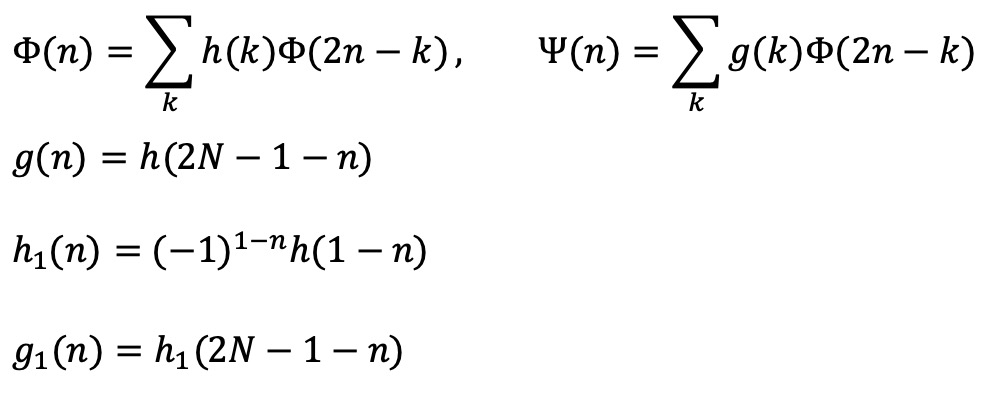
○ IDWT : 분해된 각 신호를 up-sampling 하면 입력 신호를 재구성할 수 있음
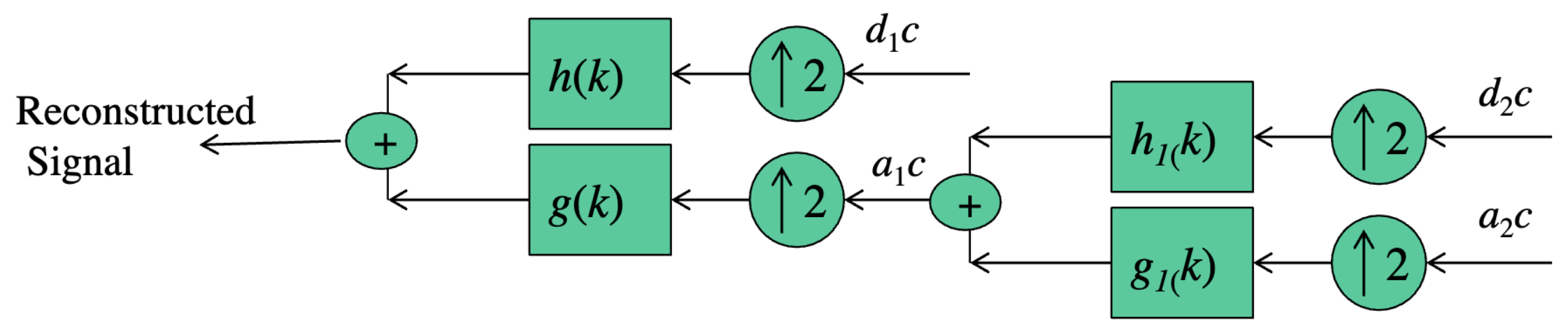
Figure. 2. IDWT의 원리
○ 2D DWT : row에서 한 번, column에서 한 번 번갈아 신호를 분해
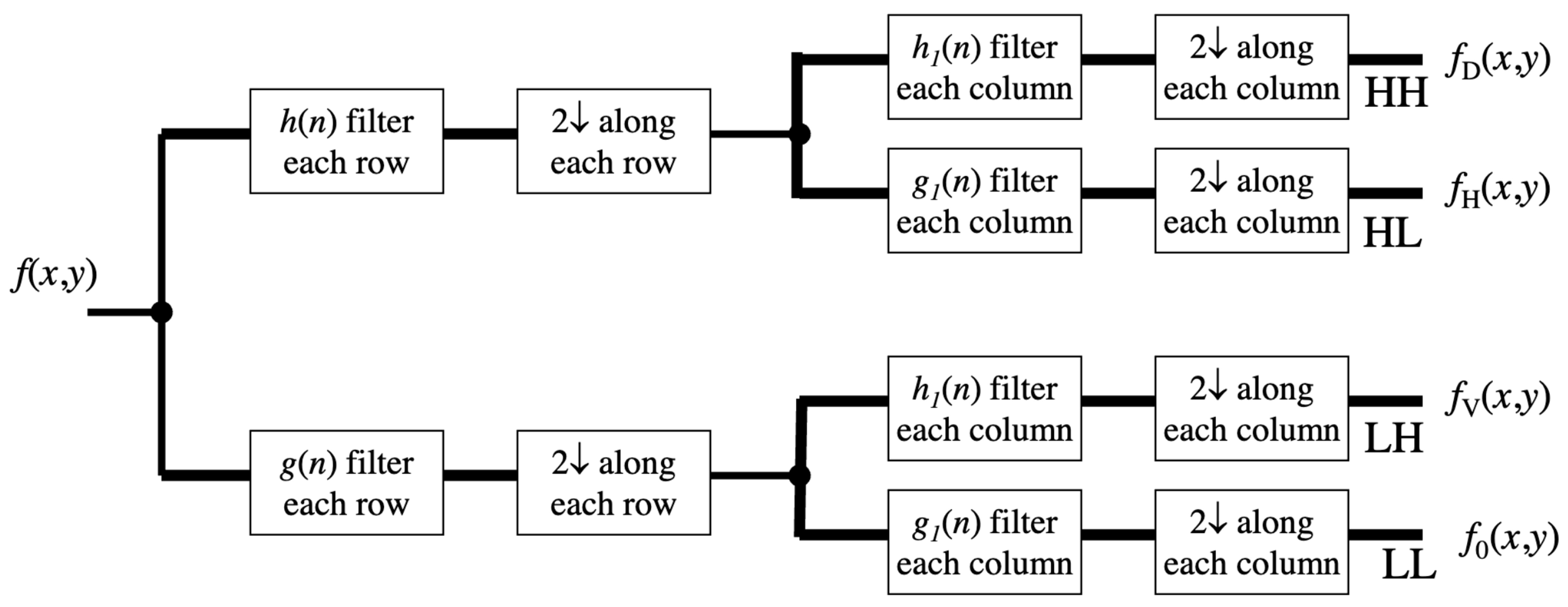
Figure. 3. 2D DWT의 원리
○ 유형
○ general wavelet decomposition : low frequency인 approximation 쪽으로만 필터링을 세분화
○ wavelet packet decomposition : high frequency인 detail 쪽으로도 필터링을 세분화하며, 트리를 구성
○ arbitrary path decomposition : low frequency 방향과 high frequency 방향을 임의로 선택하여 진행하는 방식
○ UWT(undecimated wavelet transform) : approximation이나 detail coefficient를 구할 때 원데이터의 개수를 유지
○ 응용 : 노이즈 제거(denoising), 이미지 압축(wavelet compression)
⑷ 수치적분(numeric integration) : 파형 아래 영역의 면적을 의미
① 사다리꼴 법칙(trapezoidal law) : 적분 수치해석 기법
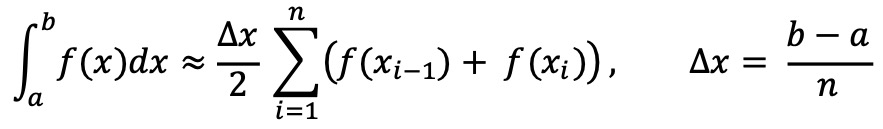
② 심슨(Simpson) 법칙 : 적분 수치해석 기법. 사다리꼴 기법에 비해 정확도가 높음
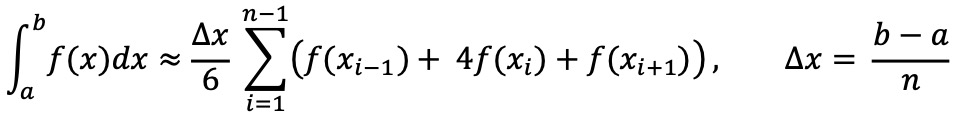
③ 심슨 3/8 법칙 : 적분 수치해석 기법. 심슨 법칙에 비해 정확도가 더 높음
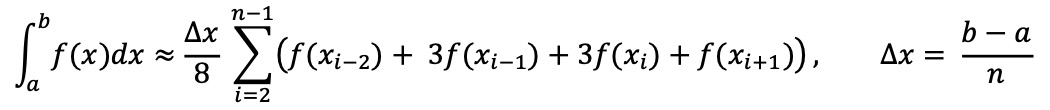
④ 보데(Bode) 법칙
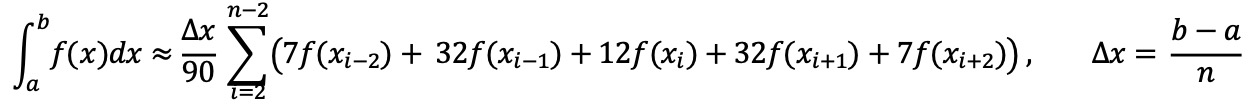
⑤ 이동평균법
⑸ MSC(multiplicative scattering correction)
① 회귀식을 만들어 보정
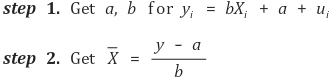
② SNV(standard normal variate) : 평균이 0이고 표준편차가 1이 되도록 정규화하는 보정
⑹ DCT(discrete cosine transformation)
① 푸리에 변환의 일종
② 오래된 버전의 JPEG은 DCT를 사용했음 : 이 버전의 JPEG은 이미지 사이즈를 90%까지 줄임
⑺ Hough transformation
① 이미지에서 각 위치와 각도에 해당하는 jet의 high signal 부분과의 교차 빈도를 분석한 것
② edg detection, angle detection 등에 활용할 수 있음
③ circle Hough transformation : 이미지에서 각 위치와 각 사이즈에 해당하는 원의 high signal 부분과의 교차 빈도를 분석한 것
⑻ Radon transformation
① Hough transformation과 비슷
② 토모그래피(tomography)에서 사용 (예 : 3D CT 이미징)
3. Nyquist theorem [목차]
⑴ aliasing artifact : 신호를 샘플링할 때 샘플링 주파수가 신호 주파수보다 낮을 경우 발생하는 왜곡 현상
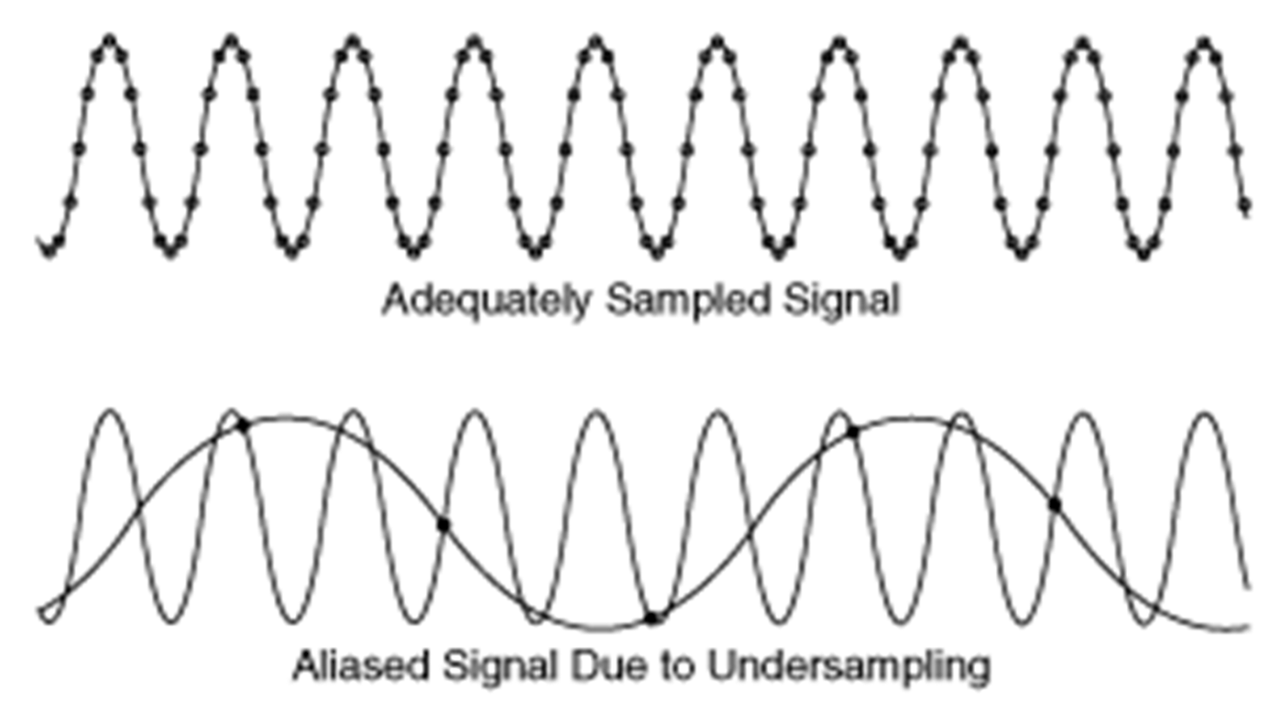
Figure. 4. aliasin artifact
⑵ Nyquist theorem : 신호의 완벽한 재구성을 위해 샘플링 주파수가 신호의 최대 주파수의 두 배 이상이어야 한다는 법칙
⑶ Nyquist theorem의 증명
① 다음과 같은 신호 x(t)와 이것의 푸리에 변환 X(f)가 주어져 있다고 가정. X(f)의 최대값을 fm이라고 정의
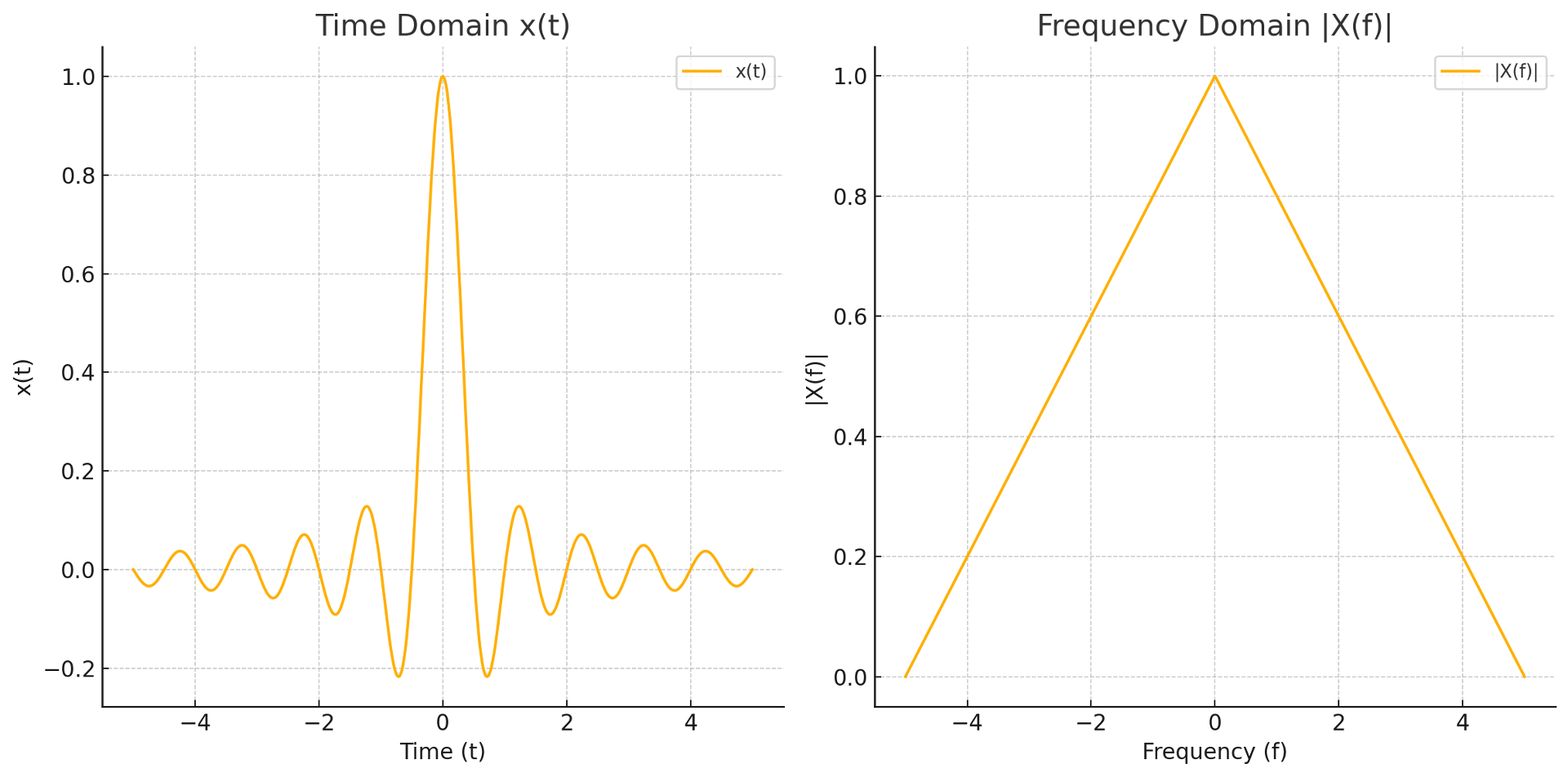
Figure. 5. x(t)와 X(f)
② 일정 시간 간격(Ts)에서만 1이고 나머지는 0인 변환함수 H(t)와 이것의 푸리에 변환 H(f)가 주어져 있다고 가정
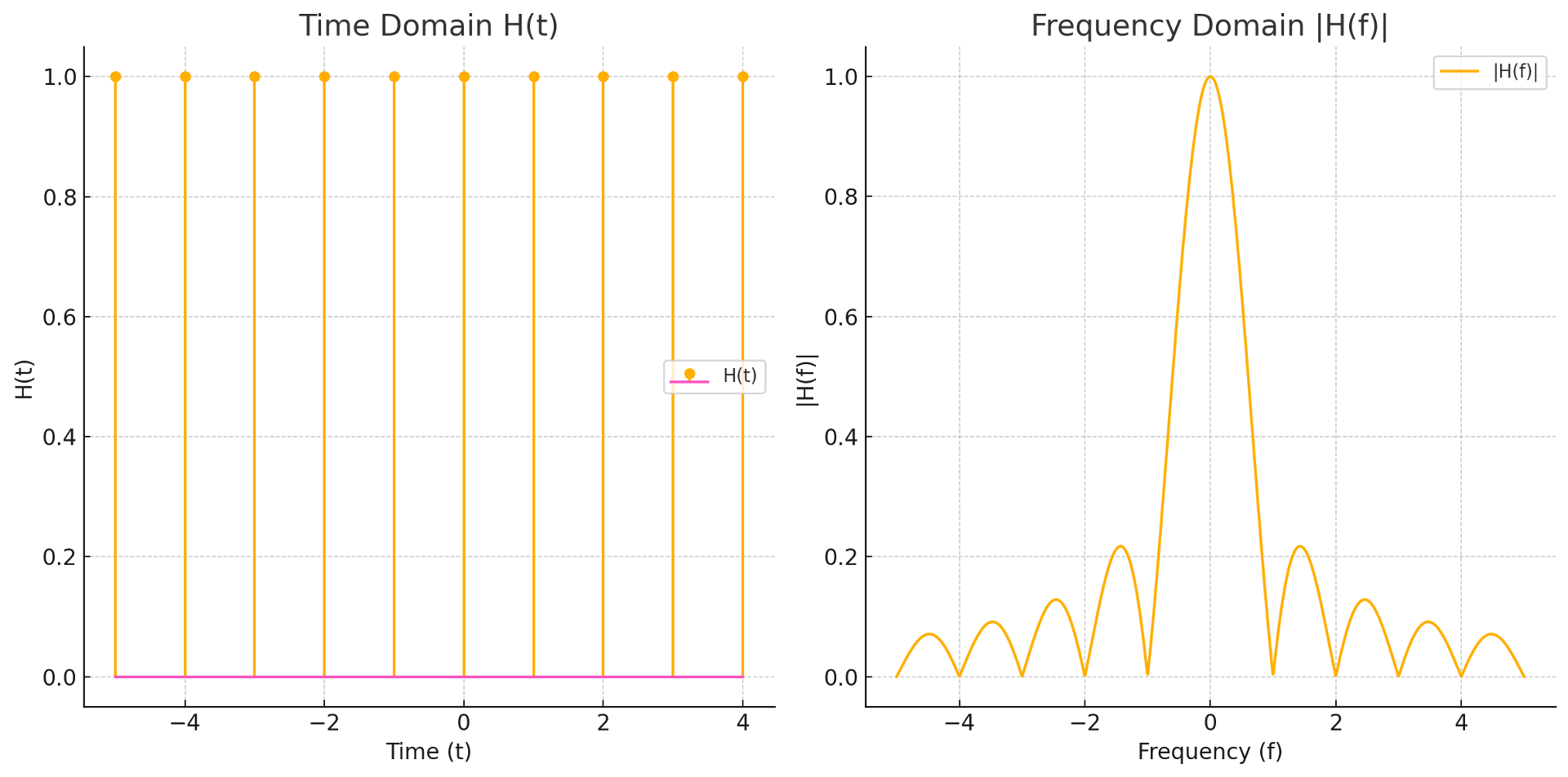
Figure. 6. H(t)와 H(f)
③ x(t)와 H(t)를 각 시간별로 곱한 것은 x(t)를 H(t) = 1일 때마다 샘플링한 것과 동일함
④ over-sampling : 신호의 주파수보다 더 빠르게 샘플링 주파수를 설정한 경우. X(f)가 fs = 1 / Ts 간격으로 띄어 있음
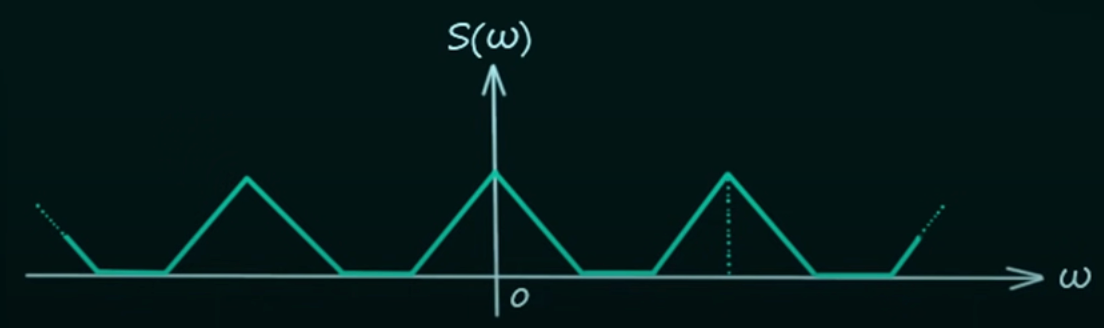
Figure. 7. over-sampling 상황
⑤ under-sampling : 신호의 주파수보다 더 느리게 샘플링 주파수를 설정한 경우. 신호 간 겹침이 발생
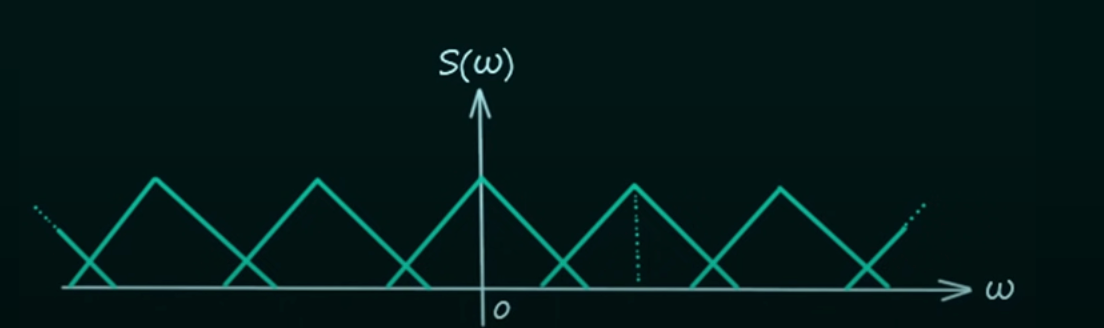
Figure. 8. under-sampling 상황
⑥ under-sampling이 되지 않기 위한 조건 : fs = 1 / Ts라고 할 때, fs - fm > fm ⇔ fs > 2 × fm
4. 필터 [목차]
⑴ 수동 필터회로
① 저역통과필터(low-pass filter) : 저주파 신호만 통과시키는 필터. blurring이 된다는 단점. smoothing filter
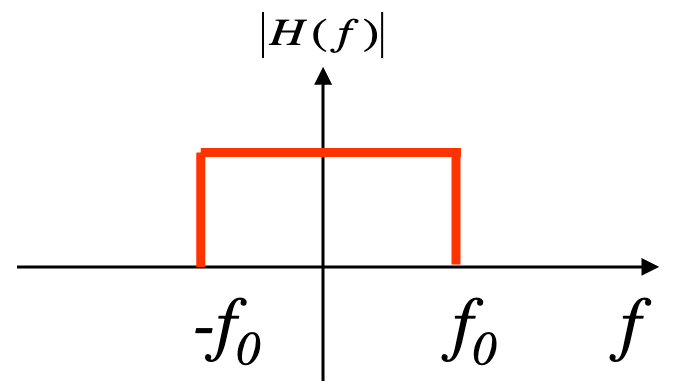
Figure. 9. 저역통과필터
② 고역통과필터(high-pass filter) : 고주파 신호만 통과시키는 필터. sharpening filter
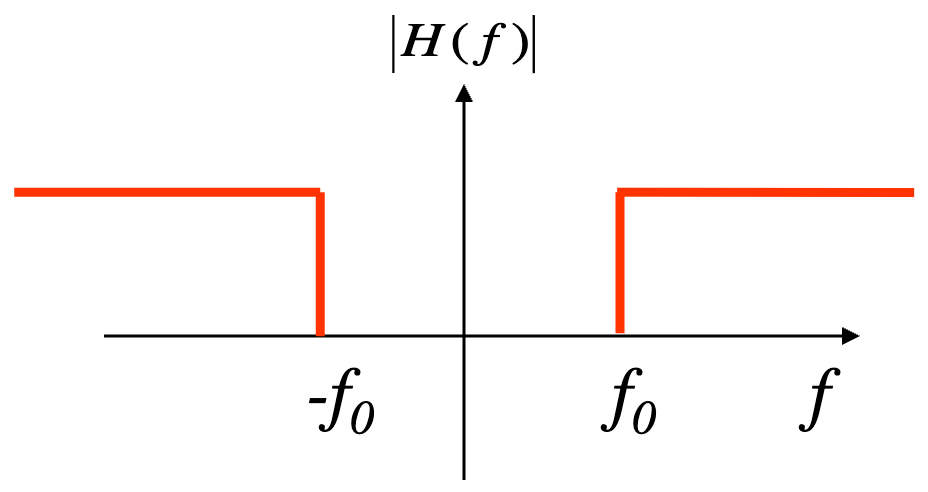
Figure. 10. 고역통과필터
③ 대역통과필터(pass-band filter) : 특정 주파수만 통과시키는 필터
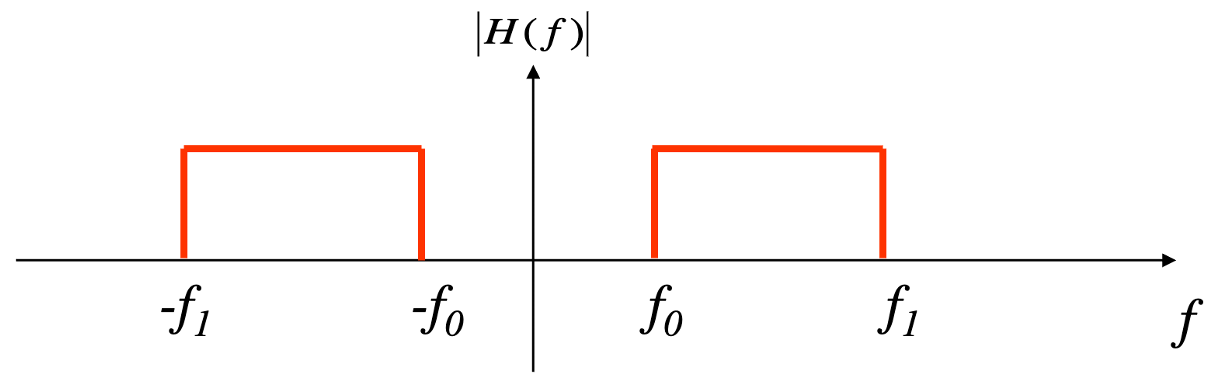
Figure. 11. 대역통과필터
④ 대역저지필터(stop-band filter, band-stop filter, notch filter) : 특정 주파수를 선택적으로 차단하는 필터
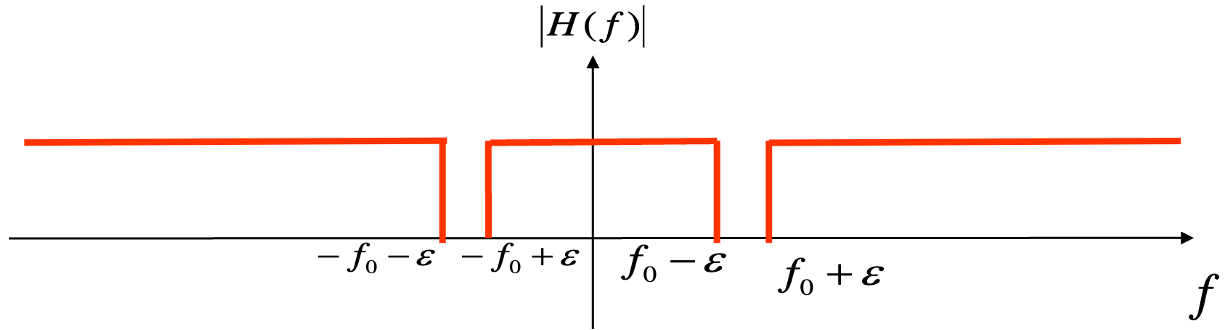
Figure. 12. 대역저지필터
⑵ 디지털 필터회로
① FIR 필터
○ 합성곱(convolution)
raw data인 {xn}에 대해, 가공 데이터 {yn}을 다음과 같이 나타낼 수 있다.
yn = b0xn + b1xn-1 + ··· + bMxn-M = ∑ bkxn-k (단, k = 0, 1, ···, M)
여기에서 bk는 매개변수 혹은 계수라고 부른다. 이때
δ(x) = 0, if x ≠ 0
δ(x) = 1, if x = 0
가 성립하는 단위 충격 함수(unit impulse function) δ(x)가 있어,
hn = ∑ bkδ(n-k) (단, k = 0, 1, ···, M) = bn, if n = 0, 1, ···, M
hn = ∑ bk δ(n-k) (단, k = 0, 1, ···, M) = 0, otherwise
yn = ∑ bkxn-k (단, k = 0, 1, ···, M) = ∑ hkxn-k (단, k = -∞, ···, ∞) = hn * xn = xn * hn
즉, yn은 hn과 xn의 합성곱(convolution)이다.
○ frequency response
모든 함수는 삼각함수의 무한한 합으로 나타낼 수 있다.
따라서 임의의 각진동수 ω, -∞ < n < ∞에 대해, xn = Aejφejωn으로 나타낼 수 있다. (ref)
따라서 k = 0, 1, ···, M에 대해 yn은
yn = ∑ bkxn-k= ∑ bke-jωkAejφejωn = ( ∑ bke-jωk ) xn = H(ejω)xn
로 나타난다.
이때, H(ejω)을 FIR 시스템의 frequency response라고 부르고 ω의 함수이다.
yn은 다시 다음과 같이 표현된다.
yn = | frequency response | e ∠frequency response xn
따라서 raw data의 진폭은 | frequency response |배가 되고, 위상은 ∠frequency response만큼 변한다.
이를 통하여 FIR 필터는 선형적인 위상 변화가 있어 위상 보정이 가능하다.
FIR 필터는 특히 위상 정보가 중요한 RF 분야나 user의 logic을 추가해야 되는 제어 등에서 많이 사용된다.
○ 예 : low-pass filter
{bk} = {1, 2, 1}인 경우, 즉 yn = xn + 2xn-1 + xn-2인 경우를 보자.
H(ejω) = ∑ bke-jωk (단, k = 0, 1, ···, M) = 1 + 2e-jω + e-2jω = (2 + 2 cosω)e-jω이므로,
| frequency response | = 2 + 2 cosω가 되어 low-pass filter가 된다.
○ Z transformation
FIR 필터를 디자인하기 위해서는 시스템의 특성과 안정성을 확인해야 한다.
그러기 위해서 Z transformation으로 시스템의 pole과 zero를 구해야 한다.
② IIR 필터
IIR 필터는 가공 데이터 {yn}을 다음과 같이 정의한다.
yn = ∑ bixn-i (단, i = 0, 1, ···, M)+ ∑ ajyn-j (단, j = 1, ···, N)
IIR 필터도 FIR 필터와 동일하게 frequency response를 통하여 주파수 특성을 확인할 수 있다.
또한 Z transformation으로 zero와 pole을 구하여 시스템을 디자인할 수 있다.
IIR 시스템은 수식이 복잡하고 계산 및 디자인이 어렵다는 단점이 있다.
또한 위상 이동이 비선형적이므로 위상 복원이 불가능하다.
그래서 위상 정보가 중요한 RF 통신에서는 이 필터를 사용하지 않는다.
하지만 진폭 특성이 다양하기 때문에 보다 이상적인 필터를 디자인할 수 있다.
③ 칼만 필터(Kalman filter)
○ 정의 : 입력신호와 출력신호가 모두 가우시안 잡음에 의해 오염될 때 바람직한 출력값을 제시하는 선형 필터
○ 종류 1. one-dimensional Kalman filter

○ uncertainty of measurement
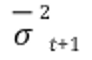
○ uncertainty of current belief
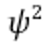
○ Kalman gain : How important the current belief is
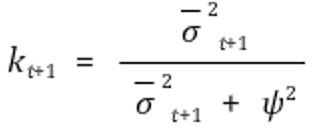
○ 종류 2. multi-dimensional Kalman filter
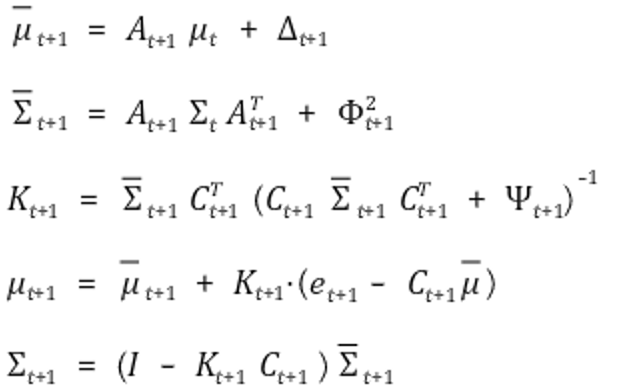
⑶ 능동 필터회로
① Sallen-Key filter
○ high pass Sallen-Key filter
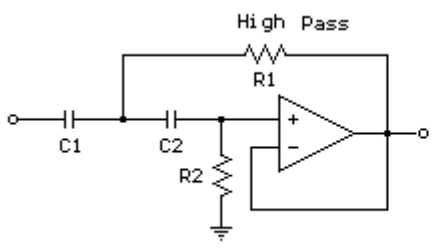
Figure. 13. high pass Sallen-Key filter
○ low pass Sallen-Key filter

Figure. 14. low pass Sallen-Key filter
② Butterworth filter

Figure. 15. Butterworth filter
○ 수식화
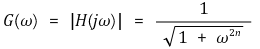
○ n : 필터의 차수. 즉, 신호가 필터를 몇 번 거치는지. n이 증가할수록 이상적인 신호인 square wave에 가까워짐
○ ω : 컷오프 주파수를 1 rad/s로 정규화시킨 것
○ 장점 : 가장 안정적인 pass-band를 가짐 (constant amplitude가 중요할 때 유리함)
○ 단점 : roll-off rate가 약함
○ 응용 : anti-aliasing application
○ (참고) roll-off rate : 신호가 주어지지 않았을 때 필터를 통과한 신호가 0으로 떨어지는 속도
③ Chebyshev filter

Figure. 16. Chebyshev Ⅰ filter

Figure. 17. Chebyshev Ⅱ filter
○ 제1형 Chebyshev filter 수식화
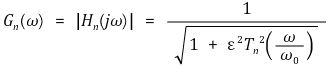
○ n : 필터의 차수. 즉, 신호가 필터를 몇 번 거치는지
○ ε : 통과대역의 ripple 크기
○ Tn : n차 Chebyshev 다항식
○ 제2형 Chebyshev filter 수식화
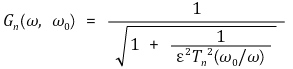
○ 장점 : roll-off rate가 가파름 (주파수 신호의 보존이 중요할 때 유리함)
○ 단점 : pass-band나 stop-band가 damping할 수 있음
④ Elliptic filter

○ 장점 : roll-off rate가 가장 가파름
○ 단점 : pass-band나 stop-band가 damping할 수 있음
⑤ Bessel filter

○ 장점 : phase response가 가장 좋음
○ 단점 : roll-off rate가 가장 나쁨
⑥ median filter
○ non-linear filter. smoothing filter
○ low-pass filter는 노이즈를 제거할 때 edge blurring이 일어나는데, median filter는 노이즈를 제거할 때 blurring이 없음
○ 이유 : 평균값이 아닌 중앙값을 이용하기 때문
⑦ HBF(high-boost filter)
○ linear filter. 수동 필터로도 구현할 수 있음. sharpening filter
○ HBF = (A - 1) × original + highpass
⑧ derivative filter
○ linear filter. 수동 필터로도 구현할 수 있음. sharpening filter
○ 종류 : Roberts mask, Prewitt mask, Sobel mask
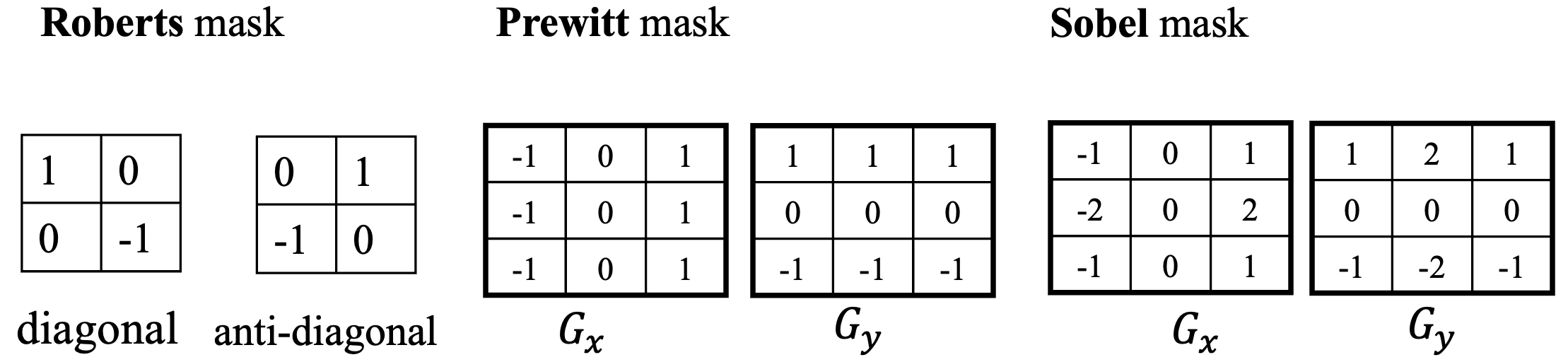
Figure. 20. Roberts mask, Prewitt mask, Sobel mask
⑨ AGF(azimuthal Gabor filter)
입력: 2018.04.29 20:35
수정: 2024.02.18 19:20
'▶ 자연과학 > ▷ 신호처리이론' 카테고리의 다른 글
| 【신호처리】 신호처리이론 목차 (0) | 2016.06.25 |
|---|

최근댓글