1강. 라플라스 변환(Laplace transformation)
추천글 : 【제어이론】 제어이론 목차
a. 라플라스 역변환 계산기
1. 개요 [목차]
⑴ 정의 : 함수 g(t) : ℝ → ℝ에 대해 g(t)의 라플라스 변환은 다음과 같이 정의. 푸리에 변환을 일반화한 것
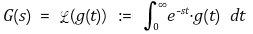
⑵ 도입 목적 : 미적분 연산을 사칙연산처럼 하기 위하여 공학자들이 도입함
⑶ 라플라스 역변환은 다음과 같이 정의

⑷ 전제 : 유한한 실수 s에 대해 g(t)는 다음을 만족해야 함
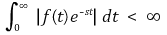
⑸ 울프람 알파(Wolfram Alpha)를 이용하여 라플라스 변환∙역반환을 확인하는 방법
① 예 : g(t) = 3t + 1의 라플라스 변환
② 예 : 1/[s(s+1)]의 라플라스 역변환
2. 주요 함수의 라플라스 변환 [목차]
⑴ 단위 임펄스함수(unit impulse function) : 디랙-델타 함수(Dirac-Delta function)이라고도 함
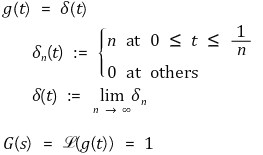
⑵ 단위 계단 함수(unit step function)
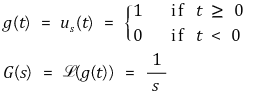
⑶ 램프 함수(ramp function)
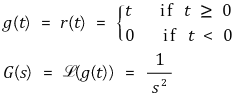
⑷ 지수함수(exponential function)
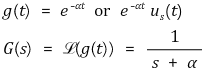
⑸ damped ramp function
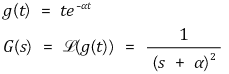
⑹ 사인함수(sine function)
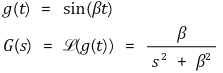
⑺ 코사인함수(cosine function)
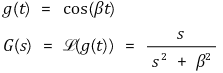
⑻ damped sine function
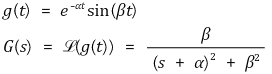
⑼ damped cosine function
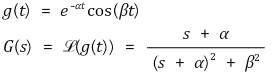
⑽ simplex complex pole (추후 업데이트)
3. 라플라스 변환의 성질 [목차]
⑴ 상수와의 곱 (multiplication by a constant)
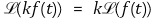
⑵ 교환법칙
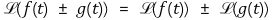
⑶ 미분(differentiation)
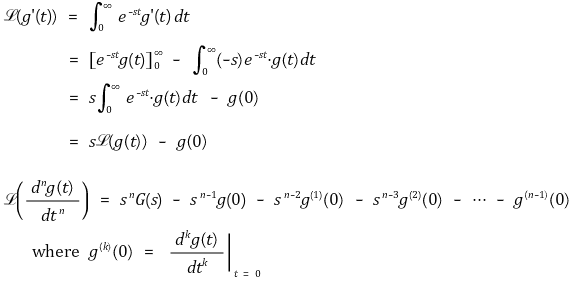
⑷ 적분(integration)
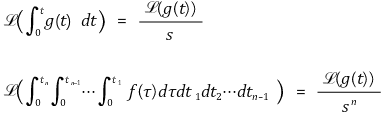
⑸ 평행이동 (shift in time)
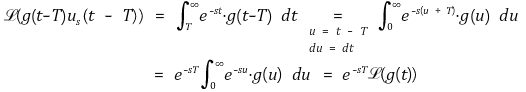
⑹ 초기값 정리(initial value theorem) : (참고) s가 붙는 이유에 대해 g(t) = C인 경우 G(s) = C / s임을 떠올리자
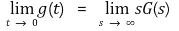
⑺ 최종값 정리(final value theorem) : (참고) s가 붙는 이유에 대해 g(t) = C인 경우 G(s) = C / s임을 떠올리자
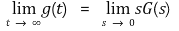
⑻ complex shifting
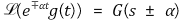
⑼ real convolution
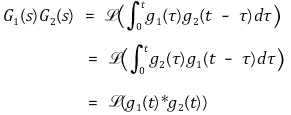
⑽ complex convolution : convolution 연산의 교환법칙이 성립함을 쉽게 보일 수 있음
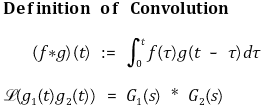
4. 영점과 극점 [목차]
⑴ 영점과 극점의 예시
① 영점(zero) : 전달함수가 유리함수로 표현돼 있을 때, 분자의 다항식이 0이 되는 s의 집합
② 극점(pole) : 전달함수가 유리함수로 표현돼 있을 때, 분모의 다항식이 0이 되는 s의 집합
③ 예시
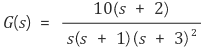
○ 영점 : -2
○ 극점 : 0, -1, -3, -3
○ 확장된 정의 : 영점을 -2, ∞, ∞, ∞으로 보기도 하는데 이는 (0·s + 1)과 관련이 있음
⑵ 극점의 형태를 통해 원래 함수의 개형을 추측할 수 있음
① 특성방정식(characteristic equation) : 전달함수의 분모가 0이 되도록 하는 방정식
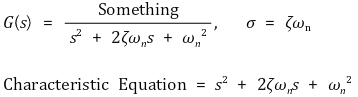
② 함수의 개형 및 시스템의 안정성

③ 특성방정식이 함수의 개형 및 시스템의 안정성과 관련 있는 이유 : t-도메인에서의 지수가 s-도메인에서의 분모가 됨
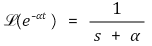
입력: 2020.04.17 08:29
'▶ 자연과학 > ▷ 제어이론' 카테고리의 다른 글
| 【제어이론】 6강. 근궤적 (2) | 2020.05.26 |
|---|---|
| 【제어이론】 5강. Time-domain Response (0) | 2020.05.02 |
| 【제어이론】 4강. 제어시스템의 안정성 (2) | 2020.04.17 |
| 【제어이론】 3강. 제어시스템의 표현 (0) | 2020.04.17 |
| 【제어이론】 2강. 제어시스템의 설계 (0) | 2020.04.17 |


최근댓글