4강. 제어시스템의 안정성
추천글 : 【제어이론】 제어이론 목차
1. 개요 [목차]
⑴ 절대적 안정성 : 주어진 시스템이 안정한지 불안정한지에 대한 기준
① 미분방정식의 해 : 과도해와 특해의 합으로 표현됨

○ 과도해(transient solution) : 입력이 0일 때의 반응. 제차해(homogeneous solution)라고도 함
○ 특해(particular solution) : 입력에 대한 반응. 정상해(steady-state solution)라고도 함
② 미분방정식을 라플라스 변환으로 변환시킨 뒤 s의 해를 구하면 σi ± jωi와 같이 표현할 수 있음
③ 유형 1. 점근적 안정(asymptotically stable) 또는 단순 안정(simply stable)
○ 정의 : 모든 극점의 실수부가 음수인 경우
④ 유형 2. 임계 안정(marginally stable) 또는 임계 불안정(marginally unstable)
○ 정의 : 한 개의 극점의 실수부가 0이고 나머지 극점의 실수부는 음수인 경우
○ 지속적인 일정 진폭진동을 일으키거나 (σ = 0, jω ≠ 0) 상수해를 가짐 (σ = 0, jω = 0)
○ 점근적 안정 또는 단순 안정을 일으키는 변수 범위의 경계조건에서 임계 안정 또는 임계 불안정
○ 예 : (s + 5)(s2 + 2)를 특성방정식으로 갖는 시스템은 s = ±jω에 의해 임계 안정
○ 예 : a < K < b에서 시스템이 안정하다면 K = a, b에서 임계 안정
⑤ 유형 3. 불안정(unstable)
○ 정의 : 한 개의 극점의 실수부가 양수인 경우
○ 공명 진동과 관련 있음
⑵ 상대적 안정성 : 한 시스템이 다른 시스템보다 얼마만큼 더 안정한지에 대한 기준
2. Routh-Hurwitz criterion : 절대적 안정성 판정 기준 [목차]
⑴ 가정 : 특성방정식이 linear time-invariant system일 것. 즉, 특정 상수에 대한 선형 결합으로 출력이 표현될 것
⑵ (참고) Routh-Hurwitz criterion의 필요조건
① (참고) 필요조건 : p → q, 즉 P ⊂ Q인 경우 q는 p의 필요조건이라고 함
② 모든 근의 실수부가 음수인 경우 다음 조건을 만족해야 함

③ 필요조건이지 충분조건은 아님 : 위 조건을 만족한다고 반드시 절대적 안정성이 있는 것은 아님
⑶ Routh's tabulation : a6, a5, A, C, E, F로 내려갈 때 sign change가 있는 횟수만큼 σi > 0인 불안정한 해가 존재함
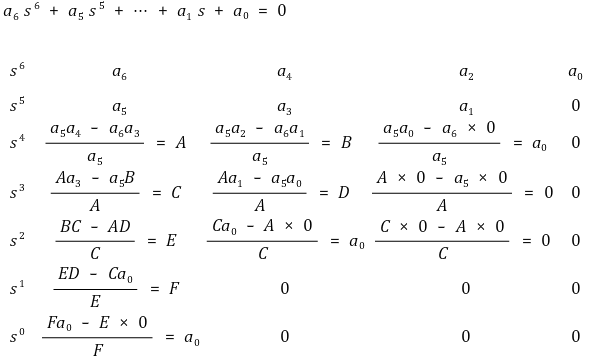
⑷ 예제 1. 아래 미분방정식은 두 개의 불안정한 해가 존재함

⑸ 예제 2. 0이 나오면 ε으로 대체해야 함 : 아래 미분방정식은 두 개의 불안정한 해가 존재함
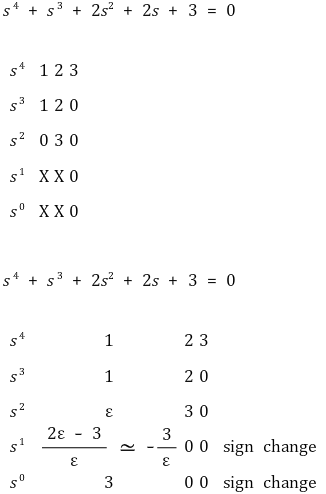
⑹ 예제 3. 0 0이 나오면 marginally stable을 의심하고 다음과 같이 unstable인지를 추가로 판정함 : 다음은 marginally stable
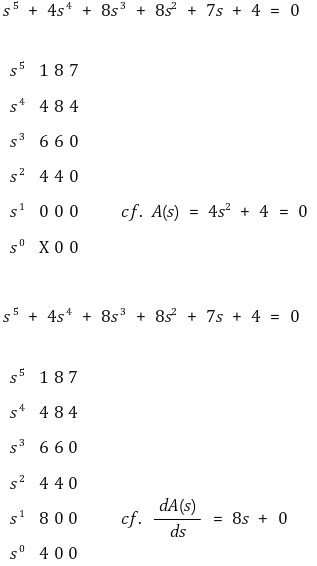
⑺ 예제 4. 비례제어기가 안정하기 위한 조건을 구할 수도 있음

3. 기타 안정성 판정법 [목차]
⑴ 근궤적법 : 근궤적을 작도하여 근의 위치가 s-plane 상의 우반면에 위치하는지 (=불안정) 판정하는 방법
⑵ Bode plot을 이용한 안정성 판정법
① 장점
○ 컴퓨터를 사용하지 않고 크기 및 위상을 근사적으로 그릴 수 있음
○ Nyquist 선도에 비해 이득교차점, 위상교차점, 이득여유, 위상여유를 구할 수 있음
○ Nyquist 선도에 비해 설계 목적을 위한 제어기 설계가 용이함
② 단점
○ 오직 최소위상시스템의 절대안정도, 상대안정도만 결정할 수 있음
○ 예를 들면 Bode 선도에서 얼마만큼 안정한가를 말할 수 없음
⑶ Nyquist plot을 이용한 안정성 판정법
① 장점
○ 절대적 안정도, 상대적 안정도, 시스템의 안정도를 개선하는 방안을 제시
○ Nyquist 선도는 컴퓨터를 이용하여 쉽게 얻을 수 있음
○ Mr, ωr, BW 등의 주파수 영역의 특성에 대한 정보를 제공
○ Routh-Hurwitz 판별법이나 근궤적법으로 해석하기 어려운 순수시간지연을 갖는 시스템에 적용 가능
② 단점
○ 주어진 Nyquist plot을 보고 시스템을 설계하기 어려움
입력: 2020.04.17 10:38
'▶ 자연과학 > ▷ 제어이론' 카테고리의 다른 글
| 【제어이론】 6강. 근궤적 (2) | 2020.05.26 |
|---|---|
| 【제어이론】 5강. Time-domain Response (0) | 2020.05.02 |
| 【제어이론】 3강. 제어시스템의 표현 (0) | 2020.04.17 |
| 【제어이론】 2강. 제어시스템의 설계 (0) | 2020.04.17 |
| 【제어이론】 1강. 라플라스 변환 (0) | 2020.04.17 |


최근댓글