6강. 근궤적(root locus)
추천글 : 【제어이론】 제어이론 목차
1. 문제 상황 [본문]
2. 극점 조사 [본문]
3. 영점 조사 [본문]
4. 독립된 근궤적의 개수 [본문]
5. 근궤적의 대칭성 [본문]
6. 점근선의 각도 [본문]
7. 점근선의 교점 [본문]
8. 근궤적과 실수축의 교점 [본문]
9. 출발각 [본문]
10. 근궤적과 허수축의 교점 [본문]
11. 이탈점 [본문]
12. K의 값 계산 [본문]
a. 근궤적 연습문제
1. 문제 상황 [목차]
⑴ 다음과 같은 전달함수를 갖는 single-loop control system의 영점의 근궤적을 구하려고 함

⑵ G1, H1, P, Q의 도입하여 특성방정식 F를 표시함 : F는 특성방정식인 Δ(s)를 의미함

① G(s)H(s) 식에 K 항이 포함돼 있어야 함
② (주석) 만약 K 항이 포함돼 있지 않으면 생략된 것이라고 생각할 것
③ 근궤적이 근에 대해 조사하는 것인 만큼 F(s) = 0 ⇔ 1 + G(s)H(s) = 0인 s를 조사
⑶ (참고) 근궤적을 지로라고도 함
2. 극점 조사 [목차]
⑴ K = 0일 때 근궤적은 G(s)H(s)의 극점으로 이동
⑵ s-plane에서 X로 표시함
⑶ 팁. 극점이 무한대일 수도 있음 : (주석) 분자의 차수가 더 높은 경우에만 해당하는 듯

Figure. 1. Ks(s2+2s+2)/(s2+5s+1)의 근궤적
(-∞, 0j)에도 극점이 있는 것으로 볼 수 있음
3. 영점 조사 [목차]
⑴ K = ∞일 때 근궤적은 G(s)H(s)의 영점으로 이동함
⑵ s-plane에서 O로 표시함
4. 분리된 근궤적의 개수(number of separate root loci) [목차]
⑴ 전체 근궤적의 개수는 F(s)의 차수와 같음 : n차 다항식의 근이 n개인 것과 관련
⑵ 예제 : 다음 s-plane에서 K = 0부터 K → ∞까지 총 세 개의 경로가 있음을 알 수 있음
![G(s)H(s) = K(s+1)/[s2(s+a)]의 근궤적](https://t1.daumcdn.net/cfile/tistory/99F0DF485EE624030F)
Figure. 2. G(s)H(s) = K(s+1)/[s2(s+a)]의 근궤적
왼쪽은 a = 9이고 오른쪽은 a = 10임
5. 근궤적의 대칭성(symmetry of root loci) [목차]
⑴ 근궤적의 대칭성은 G(s)H(s)의 극점, 영점 배치에 따라 결정됨
⑵ 예 1. F(s) = s(s+1)(s+2) + K = 0의 경우 근 궤적은 σ = -1에 대해 대칭성을 가지고 있음
⑶ 예 2. F(s) = s(s+2)(s+1+j)(s+1-j) + K = 0의 경우 σ = -1에 대해 대칭성을 가지고 있음
6. 점근선의 각도(angles of asymptotes) [목차]
⑴ n : G(s)H(s)의 유한한 극점의 개수. 중복된 근이 있어도 한 개가 아니라 똑같이 여러 개로 취급함
⑵ m : G(s)H(s)의 유한한 영점의 개수. 중복된 근이 있어도 한 개가 아니라 똑같이 여러 개로 취급함
⑶ K > 0

⑷ K < 0
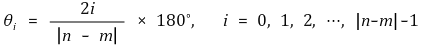
⑸ 팁. 근궤적은 점근선과 무관한 위치와 각도로 원이나 타원 같은 닫힌 궤적을 그릴 수 있음
7. 점근선의 교점(intersect of asymptotes) : 도심(centroid)이라고도 함 [목차]
⑴ 점근선의 교점은 s-plane에서 실수축에 놓임 (∵ 실수축에 대한 대칭성)
⑵ 점근선의 교점 : 중복된 근이 있어도 한 개가 아니라 똑같이 여러 개로 취급함
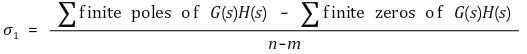
⑶ 예 1. F(s) = s(s+4)(s2+2s+2) + K(s+1) = 0의 경우 교차점의 좌표는 (σ1, 0) = (-5/3, 0)임

Figure. 3. F(s) = s(s+4)(s2+2s+2) + K(s+1) = 0의 근궤적의 점근선과 교점
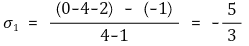
8. 근궤적과 실수축의 교점함 [목차]
⑴ s-plane의 실수축 전체는 모든 K값에 대한 근궤적 안에 포함됨
⑵ 법칙 1. 실수축에서 오른쪽에 있는 극점과 영점의 개수의 합이 홀수이면 그 실수 부분은 K ≥ 0에 대한 근궤적의 일부
⑶ 법칙 2. 실수축에서 오른쪽에 있는 극점과 영점의 개수의 합이 짝수이면 그 실수 부분은 K ≤ 0에 대한 근궤적의 일부
⑷ 극점과 영점을 중심으로 K가 증가하는 방향으로 실수축 상에 화살표를 표시할 수 있음
⑸ 만일 실수축의 한 구간에서 두 화살표가 수렴하면 그 지점에서 이탈점(breakaway point)이 발생
⑹ 예시

Figure. 4. s(s+2)(s+3) + K(s+1) = 0 (단, -∞ ≤ K ≤ ∞)의 근궤적
9. 출발각(angle of departure) : 도착각(angle of arrival)이라고도 함 [목차]
⑴ 정의 : 그 점 부근의 궤적에서 접선각. 기준은 양의 실수축
⑵ 공식 : 중복된 근이 있어도 개별적인 근인 것처럼 생각하고 계산

① 위 식은 s-plane 상의 모든 점에서 성립함
② 일반적으로 주요 영점과 극점에서만 σ1의 값을 계산함
⑶ 유도 : 다음과 같은 오일러 공식을 이용함

⑷ 예제

Figure. 5. F(s) = s(s+3)(s2+2s+2) + K = 0의 근 궤적
① s = -1+j로부터 시작한 근 궤적의 출발 각도 결정
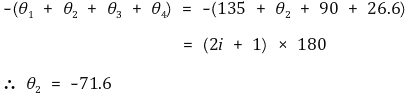
② 비슷하게 s = -1-j, -3, 0에 대해서도 출발 각도를 결정할 수 있음
⑸ 팁. 중근인 극점이나 영점에서도 출발극을 정의할 수 있음은 자명
⑹ 팁. 실수축 표시 덕분에 실수축에 있는 영점, 극점에 대해서 출발극, 도착극을 표시하지 않아도 됨
⑺ 팁. 출발각은 극점이나 영점에 국한되지 않음
10. 근궤적과 허수축의 교점 [목차]
⑴ Routh-Hurwitz criterion에서 marginally stable하게 되는 K의 값을 구함
⑵ 팁. 안정성이 깨지는 최초의 K에만 관심이 있음
⑶ (주석) 허수축의 교점이 2개보다 많은 경우 어떤 Routh's tabulation이 그려질 지 조사해볼 필요가 있음
11. 이탈점(breakaway point) : 안장점이라고도 함 [목차]
⑴ 정의 : jω 성분을 가지는 근이 생기기 시작하는 지점
⑵ G1(s)H1(s)의 변화율이 0인 지점을 찾아야 함
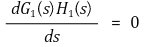
① 이탈점이 복소수일 수도 있음을 유의
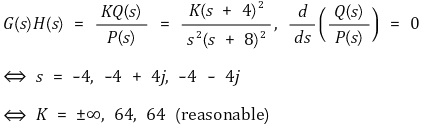
② 모든 복소수가 허용되는 것은 아님 (∵ K가 복소수를 취하는 조건일 수도 있기 때문)
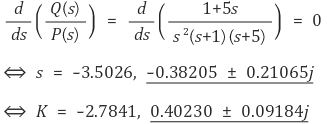
⑶ 1 + KG1H1(s) = 0이므로 dK/ds = 0인 지점을 찾는 것과 필요충분조건
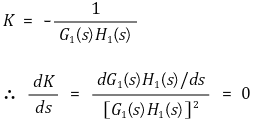
⑷ 팁. 위 방식은 중근을 가지는 극점에서 이탈하는 경우를 설명하지 못함
① 이유 : 미분한 s에 대한 방정식에서 분모, 분자가 모두 0이 되어 특이점이 됨
② 근거 1. 실수축 상의 화살표 표시로 인해 중근을 가지는 실수축 상의 극점 또는 영점에서 이탈하는 것은 자명함
③ 근거 2. 출발각을 표시하면 중근을 가지는 극점 또는 영점에서 이탈하는 것은 자명함 : 2θ의 관계식으로 표시됨
④ 제안 : P(s)에 중근이 있으면 극점에서 이탈하는 것으로 보자!
12. K의 값 계산 : 임의의 s1에 대하여, [목차]
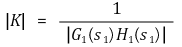
입력: 2020.05.26 14:30
'▶ 자연과학 > ▷ 제어이론' 카테고리의 다른 글
| 【제어이론】 8강. 제어시스템의 설계 (4) | 2020.06.09 |
|---|---|
| 【제어이론】 7강. Frequency-domain Response (4) | 2020.06.09 |
| 【제어이론】 5강. Time-domain Response (0) | 2020.05.02 |
| 【제어이론】 4강. 제어시스템의 안정성 (2) | 2020.04.17 |
| 【제어이론】 3강. 제어시스템의 표현 (0) | 2020.04.17 |




최근댓글