7강. Frequency-domain Response
추천글 : 【제어이론】 제어이론 목차
1. 보데 플롯(Bode plot) [목차]
⑴ 정의 : 가로축을 ω, log10ω 또는 ω / ωn으로 표시하고, 세로축을 | M(jω) | 또는 | M(jω) | (dB)로 표시한 그래프

Figure. 1. ω 대 | M(jω) | 그래프와 ω 대 φM(jω) 그래프

⑵ 장점
① 컴퓨터를 사용하지 않고 크기 및 위상을 근사적으로 그릴 수 있음
② Nyquist 선도에 비해 이득교차점, 위상교차점, 이득여유, 위상여유를 구할 수 있음
③ Nyquist 선도에 비해 설계 목적을 위한 제어기 설계가 용이함
⑶ 단점
① 오직 최소위상시스템의 절대안정도, 상대안정도만 결정할 수 있음
② 예를 들면 Bode 선도에서 얼마만큼 안정한가를 말할 수 없음
⑷ 주요 파라미터 : 표준형 2차 시스템을 중심으로 설명

① resonant frequency ωr : | M(jω) |가 최대가 될 때의 주파수
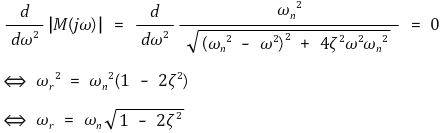
② resonant peak Mr : | M(jω) |의 최댓값
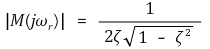
③ bandwidth BW : 주파수가 0일 때의 | M(jω) |의 1/√2, 70.7% 또는 -3 dB에 해당하는 구간
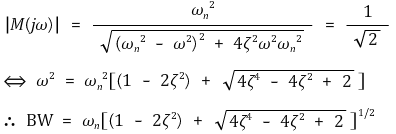
④ cutoff rate : 고주파 대역에서 ω 대 | M(jω) | 그래프의 기울기. 일반적으로 그 기울기가 일정하게 나타남
⑤ 위 resonant frequency 관계식으로부터 공명이 일어나기 위한 ζ의 조건을 발견할 수 있음
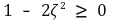
⑸ time-domain response와 frequency-domain response의 비교

Figure. 2. time-domain response와 frequency-domain response의 비교
① frequency-domain response는 지수적으로 나타나기 때문에 | M(jω) |를 일반적으로 dB 단위로 나타냄
② 위와 같은 frequency-response를 보여주는 것을 low-pass filter라고 함 : 낮은 주파수의 신호만 통과시킴
⑹ 응용 1. Bode plot을 통한 시스템 형의 결정
① 제0형 시스템의 Bode plot
○ ω → 0으로 보낼 때 ω 대 magnitude 그래프의 기울기가 0이 됨
○ (참고) 정상상태 오차는 ω → 0으로 보내면 알 수 있음
○ ω → 0으로 보낼 때 수렴하는 위상값은 0 deg : G(jω)가 양의 실수가 되기 때문

Figure. 3. 100/(s+10)의 Bode plot
② 제1형 시스템의 Bode plot
○ ω → 0으로 보낼 때 ω 대 magnitude 그래프의 기울기가 -20 dB / decade이 됨
○ ω → 0으로 보낼 때 수렴하는 위상값은 -90 deg : G(jω)가 양수 / j 꼴이 되기 때문

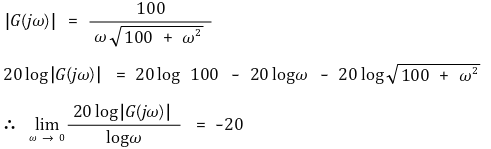
③ 제2형 시스템의 Bode plot
○ ω → 0으로 보낼 때 ω 대 magnitude 그래프의 기울기가 -40 dB / decade이 됨
○ ω → 0으로 보낼 때 수렴하는 위상값은 -180 deg : G(jω)가 음의 실수가 되기 때문

Figure. 5. 100/(s2(s+10))의 Bode plot
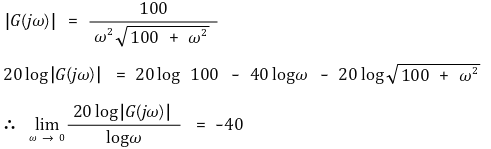
⑺ 응용 2. Bode plot을 통한 gain margin과 phase margin의 결정 (Nichols plot 참고)
2. 나이키스트 플롯(Nyquist plot) : polar plot이라고도 함 [목차]
⑴ 개요
① 정의 : ω를 0부터 ∞로 변화시켜가면서 극좌표계 상에서 가로축을 위상(phase), 세로축을 | M(jω) | (dB)로 표시한 그래프
② 전제 : 개루프 전달함수를 G(s), 피드백 요소를 H(s), 특성방정식을 Δ(s)라 하고, L(s)를 Δ(s) - 1로 정의
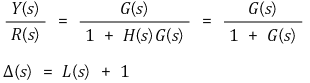
⑵ 장점
① 절대적 안정도, 상대적 안정도, 시스템의 안정도를 개선하는 방안을 제시
② Nyquist 선도는 컴퓨터를 이용하여 쉽게 얻을 수 있음
③ Mr, ωr, BW 등의 주파수 영역의 특성에 대한 정보를 제공
④ Routh-Hurwitz 판별법이나 근궤적법으로 해석하기 어려운 순수시간지연을 갖는 시스템에 적용 가능
⑶ 단점
① 주어진 Nyquist plot을 보고 시스템을 설계하기 어려움
⑷ Nyquist의 안정도 판별법
① 편각원리(argument principle) : 복소함수론에서 잘 알려져 있는 원리
○ 일주(encircled) : 복소평면 상에서 한 점이나 영역이 한 폐경로의 내부에 위치하는 경우 그 폐경로에 의해 일주됨

A는 한 번, B는 두 번 일주됨
○ 포함(enclosed) : 일주하는 폐경로의 방향에 대해 왼쪽에 놓이는 영역

Figure. 7. 폐경로에 의해 포함된 영역을 음영으로 표시한 것
○ s 평면에서 임의로 택한 폐경로 Γs와 Δ(s) 평면에서 대응하는 궤적 ΓΔ

Figure. 8. s 평면에서 임의로 택한 폐경로 Γs와 Δ(s) 평면에서 대응하는 궤적 ΓΔ
○ 편각원리
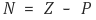
○ 전제 : Δ(s)가 단사함수일 것
○ N : Δ(s) 평면의 궤적 ΓΔ가 원점을 일주하는 횟수
○ Z : s 평면에서 s 평면의 궤적 Γs가 Δ(s)의 영점을 일주하는 횟수
○ P : s 평면에서 s 평면의 궤적 Γs가 Δ(s)의 극을 일주하는 횟수
○ Δ(s)의 극들은 음의 위상에 기여하고 영점들은 양의 위상에 기여하므로 N 값은 Z와 P의 차에 의해 결정
○ 위상의 의미 : (주석) 엄밀하게 이해하려고 하지 말고 다음과 관련 있단 것만 이해하면 족함
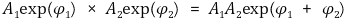
○ 편각원리의 직관적 이해

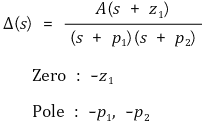
○ s1을 조절시켜 가면서 Γs를 그릴 때, (s1 + p1)과 (s1 + p2) 벡터는 일정 만큼 갔다가 원 상태로 돌아옴
○ s1을 조절시켜 가면서 Γs를 그릴 때, (s1 + z1) 벡터는 한 바퀴를 완성시킴
○ Δ(s1)은 한 바퀴를 완성시킨 (s1 + z1) 벡터 덕분에 한 바퀴를 완성시킴
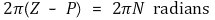
② Nyquist 경로(Nyquist path) : 시스템의 안정성을 판단하기 위해 Nyquist가 제안한 경로
○ 단계 1. 다음과 같이 Nyquist 경로 Γs를 정의
○ jω 축 상의 Δ(s)의 영점과 극점을 지나지 않도록 그려야 함
○ (참고) 영점과 극점 주위는 s0 + ε exp(jθ) (0 ≤ j ≤ π)와 같이 표현해서 Nyquist plot 상에 표시 가능
○ (참고) 큰 우반원은 R exp ε exp(jθ) (0 ≤ j ≤ π)와 같이 표현해서 Nyquist plot 상에 표시 가능

Figure. 10. Nyquist plot을 위한 s-plane 상의 경로 설정
○ 단계 2. Nyquist 경로에 대응하는 L(s) 선도를 L(s) 평면에 그림
○ (참고) Δ(s) = L(s) + 1임을 유의
○ 단계 3. L(s) 선도 ΓL이 (-1, j0)을 일주하는 횟수를 구함
○ (참고) Δ(s) 선도 ΓΔ의 경우 원점인 (0, j0)을 일주하는 횟수를 구해야 함

Figure. 11. Δ(s) 평면에서 N을 결정하는 예
Γs 궤적이 반시계 방향이므로 반시계 방향의 ΓΔ 궤적이 양의 방향임을 유의
○ 단계 4. Nyquist 판별은 편각원리에 의해 다음과 같이 이루어짐
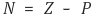
○ N : L(s) 선도 ΓL에 의해 이루어진 (-1, j0)의 일주 횟수
○ Z : s 평면 상의 Nyquist 경로에 존재하는 1 + L(s)의 영점의 수. 즉 1 + L(s) = 0이 되는 s의 수
○ P : s 평면 상의 Nyquist 경로에 존재하는 1 + L(s)의 극점의 수. 즉 1 + L(s) = ∞이 되는 s의 수
○ (참고) Z는 전달함수에게는 극점의 수임을 유의
○ (참고) 1 + L(s)의 극수는 L(s)의 극수와 같음을 유의
○ 시스템이 안정하기 위해서는 L(s)의 영점 Z가 0개가 되어야 함
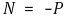
○ 즉, 폐루프 전달함수의 극점이 s 평면의 우반면에 있으면 안 됨
③ 단순화된 Nyquist의 안정도 판별법 : s 평면의 jω의 양의 축에 대해서만 Nyquist plot을 그려봐도 충분함

Figure. 12. 단순화된 Nyquist의 안정도 판별법

○ 단계 1. s 대신 jω를 대입
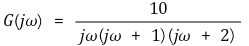
○ 단계 2. ω = ∞에 대해 조사
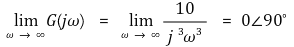
○ 단계 3. ω = 0에 대해 조사
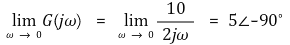
○ 단계 4. j Im G이 0일 때를 조사
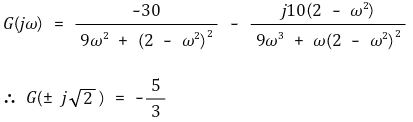
○ 단계 5. Re G이 0일 때를 조사
○ 단계 6. ω = 0일 때 실근을 조사
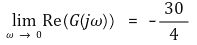
○ ΓL이 L plane의 실수축과 만나는 점이 -1보다 크면 안정, 같으면 임계 안정, 작으면 불안정
○ 팁. Nyquist plot이 연속적인 선이 아니라 발산하는 경우도 있음을 유의
![L(s) = 100/[s(s+1)(s2+2)]의 Nyquist plot](https://t1.daumcdn.net/cfile/tistory/99F898485EE814971A)
Figure. 13. L(s) = 100/[s(s+1)(s2+2)]의 Nyquist plot
④ Nyquist plot과 root locus의 관계

Figure. 14. Nyquist plot과 root locus의 관계
⑤ Nyquist plot과 time-domain plot, bode plot의 관계

Figure. 15. Nyquist plot과 time-domain plot, bode plot의 관계
⑸ gain margin과 phase margin : Nyquist plot의 형태를 설명할 수 있음
① 이득 여유(GM, gain margin) : 위상교차(phase crossover)가 일어날 때의 위상각

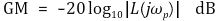
○ 위상교차(phase crossover)가 일어날 때의 주파수를 위상교차 주파수라고 함
○ | L(jωp) | < 1, GM > 0 dB : 안정
○ | L(jωp) | = 1, GM = 0 dB : 임계 안정
○ | L(jωp) | > 1, GM > 0 dB : 불안정
② 위상 여유(PM, phase margin) : 이득교차(gain crossover)가 일어날 때의 위상각

○ 이득교차(phase crossover)가 일어날 때의 주파수를 이득교차 주파수라고 함
○ 즉 | L(jωg) | = 1일 때의 위상각
○ 시스템이 불안정할수록 PM이 작아짐
⑹ 순수시간지연을 갖는 Nyquist plot
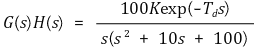
① (참고) 복소수에 exp(jφ)를 곱해주는 것은 φ만큼 반시계 방향으로 회전시킨다는 회전변환의 의미를 가짐
② 문 1. K = 1일 때 폐루프시스템이 안정하기 위한 최대시간지연 Td
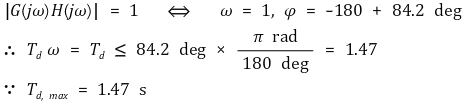
③ 문 2. 시간지연 Td가 1초일 때 시스템이 안정하기 위한 K의 최댓값
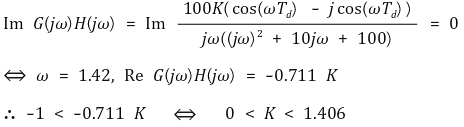
3. 니콜스 플롯(Nichols plot) : Magnitude-phase plot이라고도 함 [목차]
⑴ 정의 : ω를 매개변수로 하여 직교좌표계 상에서 가로축을 위상(phase), 세로축을 | M(jω) | (dB)로 표시한 그래프
⑵ (참고) Bode plot을 통한 gain margin과 phase margin의 결정

Figure. 18. Bode plot을 통한 gain margin과 phase margin의 결정
① 단계 1. ω 대 | L(jω) | 그래프와 ω 대 ∠L(jω) 그래프를 나란히 배치함
② 단계 2. gain margin의 계산 : ∠L(jω) = -180°인 지점의 ω를 결정하고 (ωp) 그 때의 gain을 결정
③ 단계 3. phase margin의 계산 : | L(jω) | = 0 dB인 지점의 ω를 결정하고 (ωg) 그 때의 phase를 결정
④ 루프이득은 | L(jω) |을 변화시킬 뿐 ∠ L(jω)를 변화시키지 않음
⑤ 순수시간지연은 ∠ L(jω)를 변화시킬 뿐 | L(jω) |을 변화시키지 않음
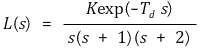
⑶ Nichols plot

① 단계 1. gain margin의 계산 : phase= -180°인 지점의 gain을 결정
② 단계 2. phase margin의 계산 : magnitude = 0 dB인 지점의 phase 변화를 결정
⑷ Nichols plot에서 gain이 일정한 점들의 집합

Figure. 20. Nichols plot에서 gain이 일정한 점들의 집합
⑸ Nichols plot의 해석

Figure. 21. 여러 가지 K 값에 따른 Nichols plot
① G(jω)/K
○ G(jω) 자체는 K를 포함하고 있음 : G(jω) / K에서 K는 약분되어 K = 1인 것과 같은 상황
○ K가 10 dB이면 G(jω) 선도는 위 G(jω) / K 선도에서 10 dB만큼 위로 평행이동
○ K가 10배이면 G(jω) 선도는 위 G(jω) / K 선도에서 20 dB만큼 위로 평행이동
② K = 1일 때
○ 이득교차 주파수 ωg = 8 rad/sec
○ 위상교차 주파수 ωp = 20 rad/sec
○ 이득여유 GM = 10 dB (∵ ω = 20 rad/s일 때 -180.0 deg이고 이때 gain이 -10.00 dB임)
○ 위상여유 PM = 57 deg (∵ ω = 8 rad/sec일 때의 각도와 -180.0 deg의 차이)
○ 공명주파수 ωr : 3 rad/s (∵ 가장 작은 원과 접해야 함)
○ 대역폭 BW : 15 rad/s (∵ 0 rad/s부터 gain이 0.707까지인 주파수 15 rad/s까지)
○ 첨두공진치 Mr
③ 임계안정
○ -180 deg에서 gain = 0 dB인 순간
○ K = 10 dB이면 ω = 8 rad/s에서 0 dB, -180 deg임을 알 수 있음
④ 정상상태 오차 : 위 시스템은 ω → 0일 때 위상이 -90 deg이므로 제1형 시스템. 따라서 ess = 0.
⑤ (참고) maximum overshoot은 time-domain에서만 구할 수 있음
입력: 2020.06.09 11:42
'▶ 자연과학 > ▷ 제어이론' 카테고리의 다른 글
| 【제어이론】 제어이론 목차 (4) | 2020.06.13 |
|---|---|
| 【제어이론】 8강. 제어시스템의 설계 (4) | 2020.06.09 |
| 【제어이론】 6강. 근궤적 (2) | 2020.05.26 |
| 【제어이론】 5강. Time-domain Response (0) | 2020.05.02 |
| 【제어이론】 4강. 제어시스템의 안정성 (2) | 2020.04.17 |




최근댓글