3강. 제어시스템의 표현
추천글 : 【제어이론】 제어이론 목차
1. 개요 [목차]
⑴ 선형 시스템 : 중첩의 원리가 적용될 수 있는 시스템 (예 : time-invariant system)
⑵ 비선형 시스템 : 중첩의 원리가 적용될 수 없는 시스템 (예 : friction system, time-varying system)
⑶ 중첩의 원리(principle of superposition) : 입력이 여러 개가 있을 때 출력은 각 입력이 단독으로 만드는 각 출력의 합임
⑷ 이득(gain) : 출력 / 입력으로 정의
2. 제어 시스템의 요소 [목차]
⑴ 요소 1. 파라미터(parameter)
① 입력(input)
② 외란(disturbance)
③ 출력(output)
⑵ 요소 2. 전달함수(transfer function)
① 개요
○ 정의 : 선형 시불변 미분방정식의 전달함수는 모든 초기조건이 0이라는 가정 하에서, 출력(응답함수)의 라플라스 변환식과 입력(구동함수)의 라플라스 변환식의 비로 정의
○ 일반적으로 입력에서 출력방향으로의 전달함수는 G로, 출력방향에서 입력방향의 전달함수를 H로 나타냄
○ 출력방향에서 입력방향의 전달함수를 피드백 요소(feedback element)라고도 함
② 다음과 같은 수학적 모델이 주어져 있다고 가정

③ 전달함수는 다음과 같음

④ 조건 : 모든 초기조건이 0이라는 것은 다음을 의미한다.
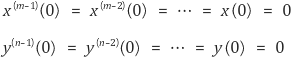
⑤ 특징 : 전달함수는 시스템 그 자체의 성질이기 때문에 입력(또는 구동함수)의 크기나 종류에는 무관
⑶ 요소 3. 제어 방정식 (추후 업데이트)
① 동작 방정식 : 결과로 얻어지는 해
② 특성 방정식(characteristic equation)
○ 전달함수의 분모가 0이 되는 극점에 대한 방정식
○ 극점의 해는 시스템의 안정성과 관련됨 : t-도메인에서의 지수가 s-도메인에서의 분모가 됨
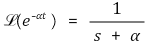
③ 상태 방정식(state equation) : 미분방정식을 연립방정식처럼 나타내어 다음처럼 나타내는 것
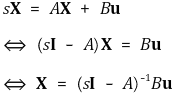
3. 표현 방법 1. 블록 다이어그램(block diagram) [목차]
⑴ 목적 : 원인-결과 관계를 잘 드러냄
⑵ 개루프 시스템(open loop system) : 피드백 없이 동작하며 입력에 대하여 직접 출력을 발생시킴
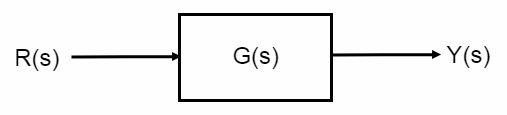
Figure. 1. 개루프 시스템

① 예 : 입력이 단위 임펄스 함수라면 Y(s) = G(s)이므로 시스템 특성을 알 수 있음
○ 이를 응용하여 헤지펀드나 투자회사에서 δ(t)를 가하여 시장 특성을 파악한 뒤 최선의 의사결정을 수행함
⑶ 폐루프 시스템(closed loop system) : 궤환제어 시스템(feedback control)이라고도 함
① 피드백을 통해 출력값을 기준입력(목표값)과 비교하여 편차를 계산
② 이 편차를 없애주거나 아주 작은 값으로 줄일 수 있는 제어신호를 만들어 냄
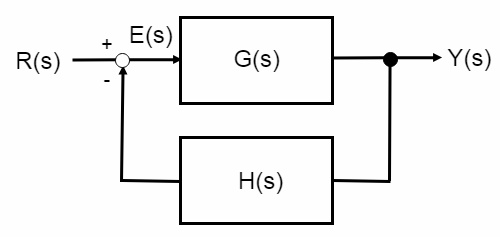
Figure. 2. 폐루프 시스템
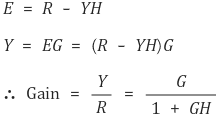
③ (주석) 위와 같은 (+, -)뿐만 아니라 (+, +), (-, +), (-, -)가 있으나 변형을 통해 (+, -)로 바꾸고 위 공식을 사용하는 것을 추천
⑷ 블록 도식의 단순화 (block diagram reduction approach)

4. 표현 방법 2. 신호흐름선도(SFG, signal flow graph) [목차]
⑴ SFG의 예시

⑵ Mason's formula : SFG로 표현하면 다음과 같은 관계식을 찾을 수 있음
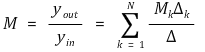
① yin : 입력 (입력이 하나만 있을 것!)
② yout : 출력
③ M : 입력과 출력에 대한 전체 이득(gain)
④ N : 후진 없이 입력 단자에서 출력 단자로 가는 경로의 수
⑤ Mk : 후진 없이 입력 단자에서 출력 단자로 가는 k 번째 경로의 이득
⑥ non-touching loop : 특정 루프와 공유하는 노드가 없는 또다른 루프
⑦ Δk : Mk 경로와 non-touching하는 loop들에 의한 Δ
⑧ Δ : 1 - (sum of the gains of all individual loops) + (sum of products of gains of all possible combinations of two nontouching loops) - ···
○ 포함-배제의 원리를 이용함
⑨ 입력 단자가 분모가 아닌 경우에 대한 전달함수를 구할 때는 입력 단자가 분모인 경우로 바꾸어서 풀 것
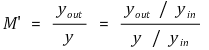
⑩ 입력이 여러 개인 경우 나머지를 0으로 두고 한 입력에 대해 Mason's formula를 적용할 것
⑶ Mason's formula 예제

① 문제 : 다른 피드백 요소로 인해 a12는 결코 아님

② N = 1
③ forward path (forward path gain으로 표시) : M1 = a12 오직 한 개
④ 모든 loop의 종류 (loop gain으로 표시) : a44, a43a34, a32a23, a24a43a32
⑤ M1 경로와 non-touching하는 loop (loop gain으로 표시) : a44, a43a34
⑥ Δ1 : a44 loop와 a43a34 loop는 nontouching loop 관계가 아니므로 (sum of products of gains of all possible combinations of two nontouching loops) 이후의 항은 0이 됨
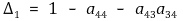
⑦ Δ : (sum of products of gains of all possible combinations of two nontouching loops) 항이 존재함
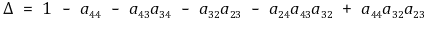
⑧ 결론
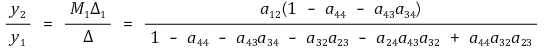
⑷ 어느 두 루프도 non-touching loop가 아닌 경우 Mason's formula는 다음과 같이 변형될 수 있음
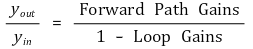
⑸ (주석) Mason's formula 때문에 블록 다이어그램보다 신호흐름선도를 더 많이 사용함
입력: 2018.09.11 22:54
수정: 2020.03.24 11:47
'▶ 자연과학 > ▷ 제어이론' 카테고리의 다른 글
| 【제어이론】 6강. 근궤적 (2) | 2020.05.26 |
|---|---|
| 【제어이론】 5강. Time-domain Response (0) | 2020.05.02 |
| 【제어이론】 4강. 제어시스템의 안정성 (2) | 2020.04.17 |
| 【제어이론】 2강. 제어시스템의 설계 (0) | 2020.04.17 |
| 【제어이론】 1강. 라플라스 변환 (0) | 2020.04.17 |




최근댓글