광학 2강. 파동광학
추천글 : 【물리학】 물리학 목차
1. 호이겐스의 원리 [본문]
2. 페르마 원리 [본문]
3. 슬릿 실험 [본문]
4. 전자기파 [본문]
1. 호이겐스의 원리(하위헌스의 원리, Huygen's principle) [목차]
⑴ 원리 : 파면 상의 모든 점이 파원이 되어 새로운 파면을 만듦
⑵ 직진의 원리
① 현대 양자광학에서 원자들이 점파원이 됨
② 의문 : 광자가 원자에게 흡수된 뒤 다시 방출된다면 빛은 왜 직진만 하는가? 왜 뒤로 안 가는가?
③ 답변 : 마치 초음속 충격파처럼 전방은 모두 보강간섭이지만 다른 경로는 상쇄간섭을 함
⑶ 반사의 법칙
① 증명
Figure. 1. 호이겐스의 원리에 따른 반사의 법칙 증명
○ 전제 1. 직진의 원리에 의해 O, P'', Q''은 동일한 위상을 가짐
○ 전제 2. O, P'', Q''으로부터 동일한 시간 뒤에 생긴 파원 O', P', Q는 동일한 위상을 가짐
○ 전제 3. O, P, Q는 동일한 위상차를 가짐
○ 결론 : θ = θ'

② 반사의 법칙을 따르지 않는 빛은 상쇄간섭 때문에 사라짐
③ 고정단 반사(fixed end reflection) : 매질의 굴절률이 낮은 곳에서 높은 곳으로 반사가 일어날 때
○ 파동의 위상이 π만큼 변함
④ 자유단 반사(free end reflection) : 매질의 굴절률이 높은 곳에서 낮은 곳으로 반사가 일어날 때
○ 파동의 위상이 변하지 않음
⑷ 굴절의 법칙
① 빛의 파동성에 따른 해석
Figure. 2. 호이겐스의 원리에 따른 굴절의 법칙 증명
○ 전제 1. 직진의 원리에 의해 O, P'', Q''은 동일한 위상을 가짐
○ 전제 2. O, P'', Q''으로부터 동일한 시간 뒤에 생긴 파원 O', P', Q는 동일한 위상을 가짐
○ 전제 3. O, P, Q는 동일한 위상차를 가짐
○ 전제 4. O, Q 사이의 시간차를 Δt로 정의
○ 결론
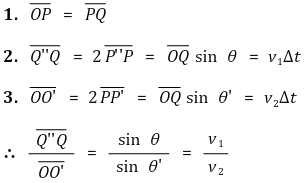
② 빛의 입자성에 따른 해석
○ 굴절의 법칙을 따르지 않는 빛은 상쇄간섭 때문에 사라짐
○ 굴절의 법칙은 광자의 에너지-운동량 관점으로 분석할 수 있음
③ 예 1. 물에 의한 빛의 굴절 : 물체가 실제 깊이보다 얕은 곳에 있는 것처럼 보임
④ 예 2. 렌즈에 의한 빛의 굴절 : 기하광학에서 자세히 기술
⑤ 예 3. 대기에 의한 빛의 굴절
○ 신기루(mirage)
○ 빛의 속력은 공기의 온도가 높을수록 느림
○ 찬 공기가 위쪽, 뜨거운 공기가 아래쪽 : 하늘에서 온 빛이 뜨거운 공기층을 통과하여 눈으로 보임
○ 찬 공기가 아래쪽, 뜨거운 공기가 위쪽 : 공중을 향하던 빛이 아래로 휘어져 물체가 공중에 뜬 것처럼 보임
○ 일출과 일몰 때 지평선 아래의 태양이 보이는 현상
○ 태양이 타원형으로 보이는 현상 : 수평선 근처에 잇는 태양은 타원형으로 보임
○ 아지랑이
○ 반짝이는 별
⑸ 회절의 원리
⑹ 체렌코프 방사선(Cherenkov radiation)
① 전하를 띤 입자가 매질 내에서 빛보다 빠른 속력으로 운동할 때 빛이 방출되는 현상
② 호이겐스의 원리에 의한 보강간섭으로 설명할 수 있음
2. 페르마 원리(Fermet's principle) : 최소 시간의 원리라고도 함 [목차]
⑴ 정의 : 두 점 사이를 진행하는 빛은 진행 시간이 가장 짧게 걸리는 경로를 택하여 진행한다는 법칙
⑵ 반사 법칙의 해석 (추후 업데이트)
⑶ 굴절 법칙의 해석 (추후 업데이트)
3. 슬릿 실험 [목차]
Figure. 3. 폭이 a이고 간격이 b인 이중슬릿
⑴ 이중슬릿(double slit) : b에 의한 회절을 관찰하는 것

① d : 슬릿 간 거리
② L : 스크린과 슬릿 간 거리
③ Δx : 중앙 지점으로부터 스크린 상의 지점 간 거리
⑵ 단일슬릿(single slit) : a에 의한 회절을 관찰하는 것
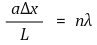
① a : 폭
② L : 스크린과 슬릿 간 거리
③ Δx : 중앙 지점으로부터 스크린 상의 지점 간 거리
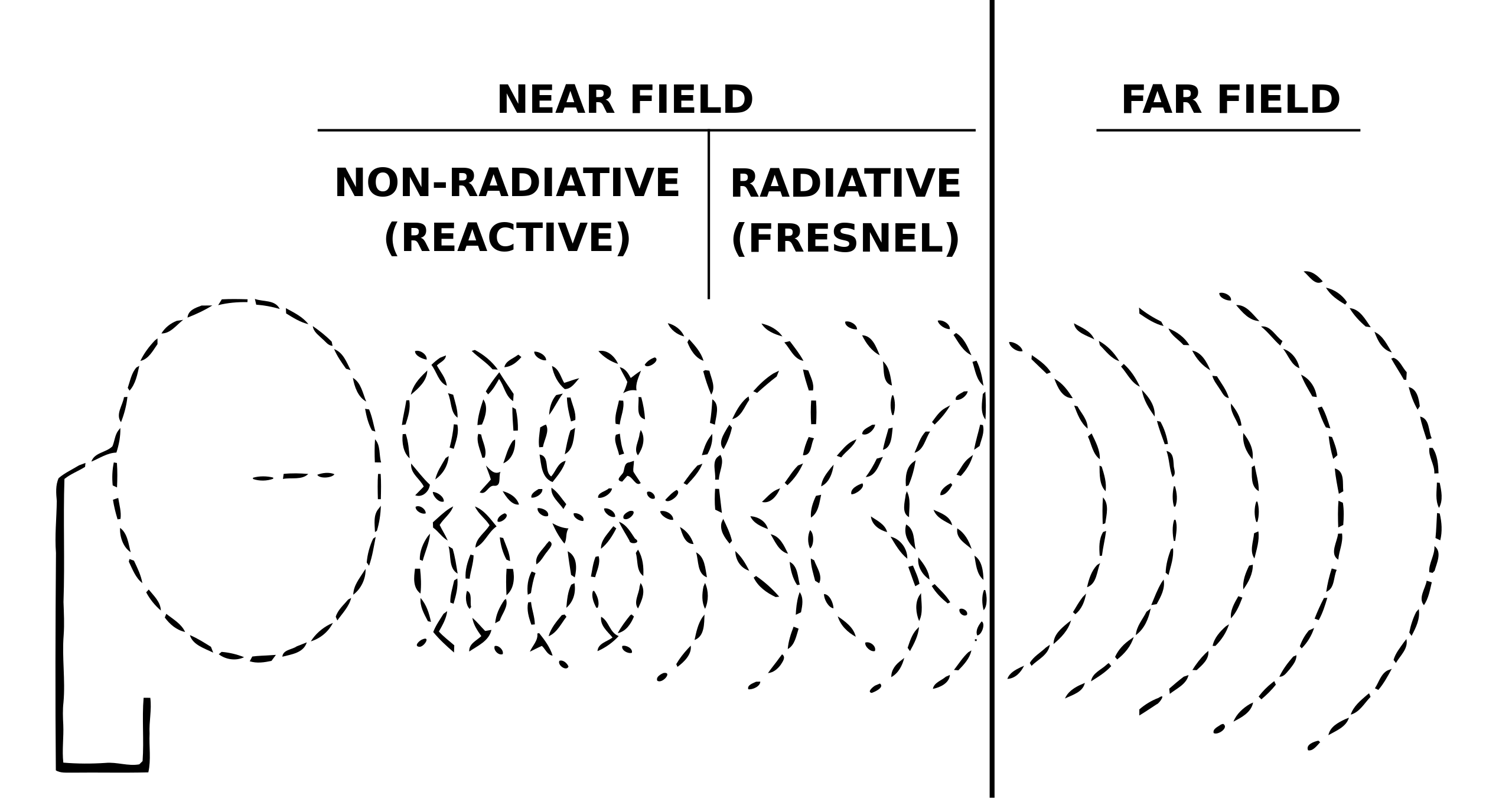
⑶ Fresnel 산란과 Fraunhofer 산란
Figure. 4. Fresnel 산란과 Fraunhofer 산란
① Fresnel 산란 : near-field 산란
② Fraunhofer 산란 : far-field 산란
③ 푸리에 변환을 활용하여 분석 : 산란을 하여도 각 빛의 위상은 바뀌지 않음을 유의
④ 응용 : 초음파 분석
4. 전자기파(electromagnetic wave) [목차]
⑴ 맥스웰 방정식(Maxwell's equation)
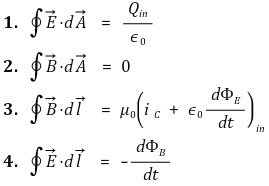
⑵ 전자기파의 파동방정식

① 위 파동방정식으로부터 전자기파의 속도 c를 유도할 수 있음
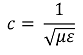
⑶ 포인팅 벡터(Poynting vector)
① 정의 : 단위 면적, 단위 시간에 통과하는 에너지
② 전자기파의 발생
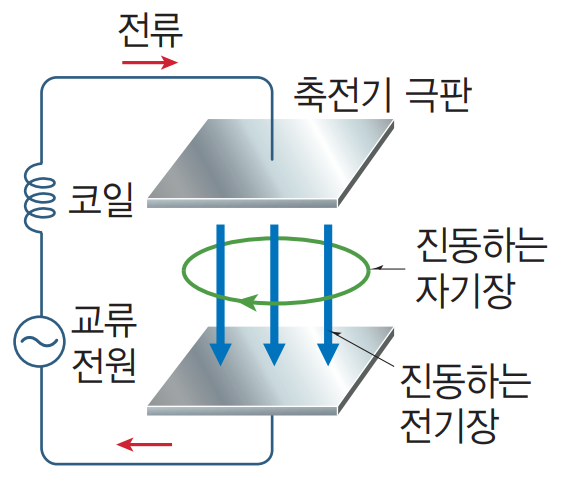
③ 수식화
○ 전자기파 전계 식
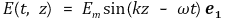
○ 전자기파 자계 식
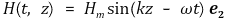
○ 전계(E), 자계(H) 공통
○ e3성분이 0
○ x에 관한 1차 도함수가 0
○ y에 관한 1차 도함수가 0
○ 맥스웰 3법칙 : 변위전류의 도입을 주목
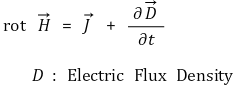
○ 맥스웰 3법칙 적용

○ 최종 포인터 벡터 식
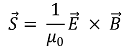
④ 유전율(permittivity)
○ 정의 : 부도체의 전기적인 특성을 나타내는 값
○ 분극현상에 의해 유전체 내 전기장 세기가 작아지는 비율
○ 일반 공기는 무시할 수 있을 정도의 도전율을 갖고 있음
○ 비오는 날은 공기의 도전성이 증가하여 감쇠가 더 심하게 나타남
⑤ 유전체 손실각
○ 정의 : 특정 주파수 f와 변위 전류와 전도 전류가 같아지는 주파수 fc에 대해 f의 유전체 손실각을 f tanθ = fc가 성립하는 θ
⑥ 고유 임피던스(Intrinsic Impedance) := Z = E / H
○ 공간의 전계 에너지 밀도 We와 자계 에너지 밀도 Wm 사이에는 다음과 같은 관계가 있다. (η : 고유 임피던스)
○ 전계의 투과계수
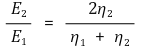
○ 자계의 투과계수 (자계 H의 단위 : AT / m)
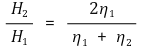
○ 반사율 = 반사 전계 세기 ÷ 입사 전계 세기
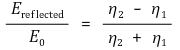
○ 매질의 변화는 μ, ε를 변화시켜, 파장, 진폭을 변화시킬 수 있을 뿐 주파수를 바꾸지는 못한다.
○ 전자파의 위상은 변위전류보다 90˚ 늦다(?)
○ Z0 = E / H가 실수이므로 E와 H의 위상이 서로 같음
⑦ 벡터 마그네틱 포텐셜(vector magnetic potential)

○ 시변계에서
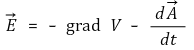
⑷ 전자기파의 종류
① γ선(γ-ray)
○ 주파수 범위 : > 8 × 1018 Hz
○ 파장 범위 : < 0.04 nm
② X선(X-ray)
○ 주파수 범위 : 8 × 1018 ~ 6 × 1016 Hz
○ 파장 범위 : 0.04 ~ 5 nm
③ 자외선(UV, ultra violet)
○ 주파수 범위 : 6 × 1016 ~ 8 × 1014 Hz
○ 파장 범위 : 5 ~ 380 nm
④ 가시광선(visible light)
○ 주파수 범위 : 8 × 1014 ~ 4 × 1014 Hz
○ 파장 범위 : 380 ~ 780 nm
⑤ 적외선(IR, infra-red)
○ 근적외선(NIR, near infra-red) : 780 ㎚ ~ 1.5 ㎛
○ 중적외선(MIR, mid infra-red) : 1.5 ㎛ ~ 5 ㎛
○ 원적외선(FIR, far infra-red) : 5 ㎛ ~ 15 ㎛
⑥ 마이크로파(microwave)
○ 주파수 범위 : 4 × 1011 ~ 8 × 1010 Hz
○ 파장 범위 : 0.75 ~ 3.75 mm
○ 쌍극자 회전, 이온분극을 일으켜 열을 발생 : 물을 데우는 원리
○ 전자레인지는 주로 2.45 GHz 주파수를 사용
⑦ T선(T-ray)
○ 주파수 범위 : 0.1 × 1012 ~ 10 × 1012 Hz
○ 파장 범위 : 30 μm ~ 1 mm
⑧ 라디오파(radio frequency)
입력: 2019.04.11 14:36
수정: 2020.04.01 16:33
'▶ 자연과학 > ▷ 일반물리학' 카테고리의 다른 글
| 【전자기학】 2강. 맥스웰 제1법칙 (0) | 2016.06.26 |
|---|---|
| 【전자기학】 1강. 전자기학의 기초 (3) | 2016.06.26 |
| 【물리학】 광학 1강. 기하광학 (0) | 2016.06.26 |
| 【물리학】 파동역학 3강. 파동방정식 (0) | 2016.06.26 |
| 【물리학】 파동역학 2강. 파동의 전파 (0) | 2016.06.26 |







최근댓글