파동역학 2강. 파동의 전파
추천글 : 【물리학】 물리학 목차
1. 파동의 반사 [본문]
2. 파동의 굴절 [본문]
3. 중첩의 원리 [본문]
4. 간섭 [본문]
5. 정상파 [본문]
6. 도플러 효과 [본문]
a. 공명 실험
1. 파동의 반사 [목차]
⑴ 고정단 반사(fixed end reflection)
① 매질이 소한 곳에서 밀한 곳으로 반사가 이루어질 때
② 파동의 위상이 π 만큼 변함
⑵ 자유단 반사(free end reflection)
① 매질이 밀한 곳에서 소한 곳으로 반사가 이루어질 때
② 파동의 위상은 바뀌지 않음
2. 파동의 굴절 [목차]
⑴ 수면파의 굴절
① 사고 실험 : 파동을 폭을 가진 선이라고 생각할 때 한쪽 끝은 빠르고 반대쪽 끝은 느리면 느린 쪽으로 굽어짐
② 결론 : 파동은 느린 쪽으로 굴절됨
⑵ 빛의 굴절
① 빛은 두께가 있고 보강간섭을 고려하면 위와 같은 사고 실험이 유효함
② 결론 : 탄성파, 입자파를 불문하고 파동은 느린 쪽으로 굴절됨
⑶ 예 1. 해안선에 나란해지는 파도
① 해안선이 오목한 곳은 바다 쪽으로 돌출된 곳보다 수심이 깊어서 오목한 곳으로 진행하는 파도의 속력이 빠름
② 결국 파도가 해안가로 다가갈수록 파면이 점점 해안선에 나란해짐
⑷ 예 2. 낮과 밤의 소리의 굴절
① 소리의 속력은 공기의 온도가 높을수록 빠름
② 낮에는 소리의 진행 방향이 위쪽으로 휘어지고, 밤에는 소리의 진행 방향이 아래쪽으로 휘어짐
⑸ 예 3. 해수 내 음속
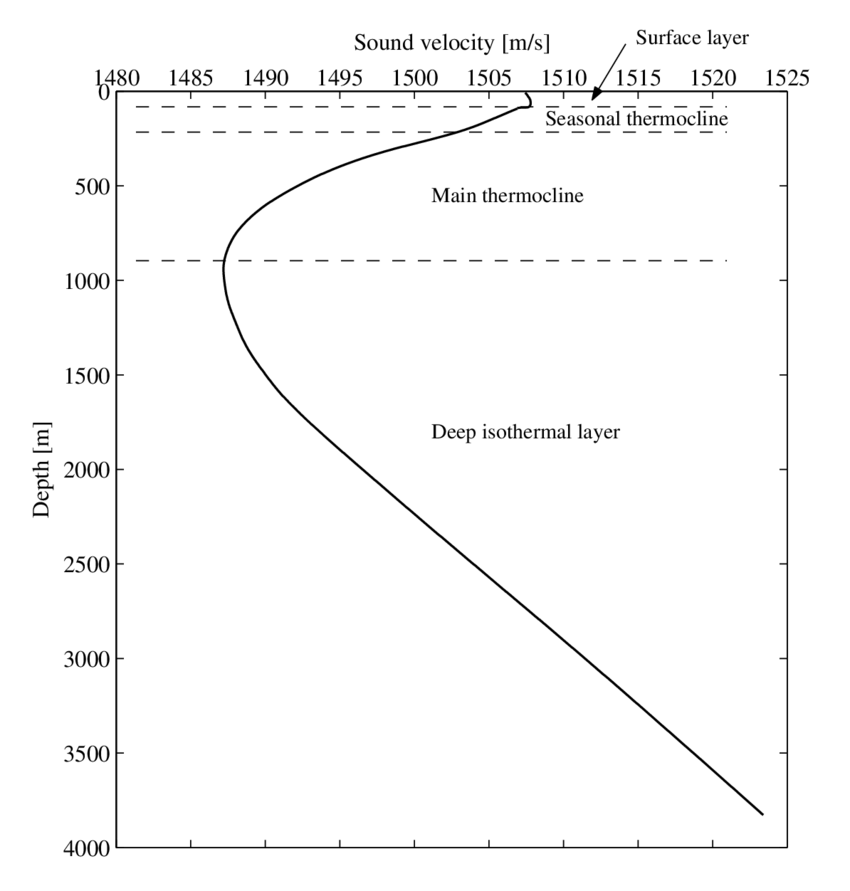
Figure. 1. deep-sea sound velocity profile
① 경우 1. 깊이 < 1,000 m : 소리는 아래쪽으로 굴절됨
② 경우 2. 깊이 > 1,000 m : 소리는 위쪽으로 굴절됨
③ 음파 채널 : 음파 채널은 1,000 m 전후에 존재함
○ 소리는 1,000 m 전후에서 파동을 그리며 해수면과 나란한 방향으로 전파됨
○ 고래나 잠수함이 자주 이용
⑹ 예 4. 물에 의한 빛의 굴절 : 물체가 실제 깊이보다 얕은 곳에 있는 것처럼 보임
⑺ 예 5. 렌즈에 의한 빛의 굴절
⑻ 예 6. 대기에 의한 빛의 굴절
① 신기루(mirage)
○ 빛의 속력은 공기의 온도가 높을수록 느림
○ 찬 공기가 위쪽, 뜨거운 공기가 아래쪽 : 하늘에서 온 빛이 뜨거운 공기층을 통과하여 눈으로 보임
○ 찬 공기가 아래쪽, 뜨거운 공기가 위쪽 : 공중을 향하던 빛이 아래로 휘어져 물체가 공중에 뜬 것처럼 보임
② 일출과 일몰 때 지평선 아래의 태양이 보이는 현상
③ 태양이 타원형으로 보이는 현상 : 수평선 근처에 잇는 태양은 타원형으로 보임
④ 아지랑이
⑤ 반짝이는 별
3. 중첩의 원리(principle of superposition) [목차]
⑴ 중첩의 원리
① 원리 1. F(x + y) = F(x) + F(y)
② 원리 2. F(ax) = aF(x)
③ F의 예 : ax, d/dx, ∫ dx
⑵ 파동 중첩의 원리
① 파동방정식
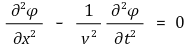
② 파동 중첩의 원리 : φ1과 φ2가 위 파동방정식의 해라면 φ = aφ1 + bφ2 또한 위 파동방정식의 해가 됨
4. 간섭(interference) [목차]
⑴ 개요
① 정의 : 중첩의 원리를 반영하는 현상
② 종류 1. 보강간섭(constructive interference) : 서로 다른 두 파동의 위상이 같아 진폭이 두 배가 되는 것
③ 종류 2. 상쇄간섭(destructive interference) : 서로 다른 두 파동의 위상이 반대가 되어 진폭이 0이 되는 것
⑵ 수학적 표현
① 오일러 표현
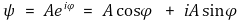
○ A : 진폭
○ eiφ : 위상
② 파동의 중첩
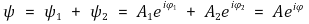
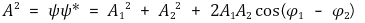
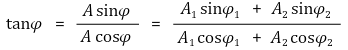
③ 파동의 간섭
○ 간섭은 일반적으로 A1 ≃ A2 = A인 상황을 지칭
○ 파동함수 Ψ
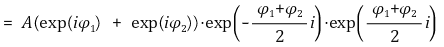
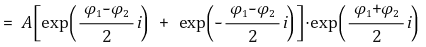
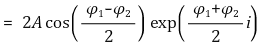
○ 진폭 : 2A cos( (φ1 - φ2) ÷ 2 )
○ 위상항 : exp( i(φ1 + φ2) ÷ 2 )
○ 간섭항 : cos( (φ1 - φ2) ÷ 2 )
○ 0 ≤ | ψ | ≤ 2A
○ 보강간섭 : Δx = nλ
○ 상쇄간섭 : Δx = (n + ½) λ
5. 정상파(standing wave) [목차]
⑴ 개요
① 정의 : 직선상에서 속도의 방향만 다른 두 파동이 연속적으로 발생하여 파동이 정지한 것처럼 보이는 것
② 마디(node) : 정상파 상에서 진동하지 않는 지점
③ 배(antinode) : 정상파 상에서 진폭이 최대가 되는 지점
⑵ 수식적 표현
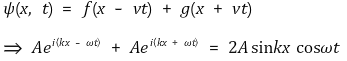
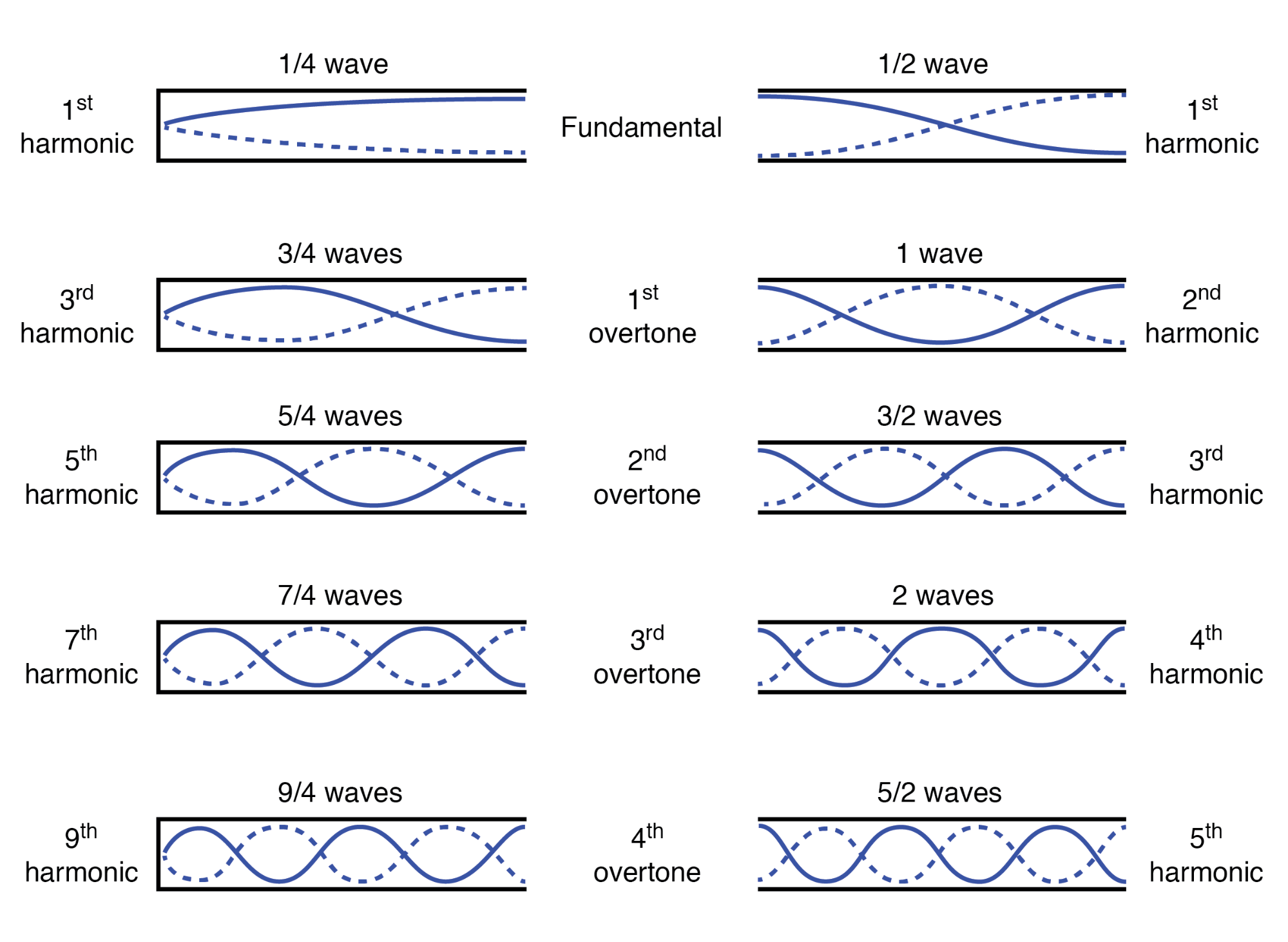
⑶ 경우 1. 현에서의 정상파
① 양쪽의 묶여 있는 지점에서는 마디가 형성됨
② 현의 길이를 ℓ이라고 하면 상태수 n에 따라 정상파를 형성하는 파동의 파장은 2ℓ / n이 됨
③ 피타고라스 음계 : 피타고라스는 무리수를 이용하여 음계를 구성함
○ 원리 1. 완전 5도 관계 : 솔은 도의 관의 길이의 2/3배임
○ 원리 2. 옥타브 : 한 옥타브 높은 도는 관의 길이가 1/2배로 줄어듦
○ 위 두 개의 원리를 이용하면 나머지 음계도 만들 수 있음
○ 해당 무리수를 가까운 분수로 나타내기도 함
⑷ 경우 2. 개관 정상파(open pipe standing wave)
① 양쪽이 열려 있는 개관에서는 관의 끝부분에서 배가 형성됨
② 관의 길이를 ℓ이라고 하면 상태수 n에 따라 정상파를 형성하는 파동의 파장은 2ℓ / n
⑸ 경우 3. 폐관 정상파(closed pipe standing wave)
① 한쪽만 열려 있는 폐관에서는 막힌 쪽은 마디, 열린 쪽은 배가 형성됨
② 관의 길이를 ℓ이라고 하면 상태수 n에 따라 정상파를 형성하는 파동의 파장은 4ℓ / (2n - 1)
6. 도플러 효과(Doppler effect) [목차]
⑴ 수식화
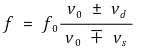
① vs : 파원(예 : 음원)의 속력
② vd : 관측기의 속력
③ v0 : 파동(예 : 음파)의 속력
④ f0 : 파동의 주파수
⑤ f : 관측 주파수
⑥ (주석) 부호 판정은 직관적으로 할 것
⑵ 음원이 움직이는 경우 : 파동의 측정 파장은 달라지고 측정 속도는 일정함
⑶ 측정기가 움직이는 경우 : 파동의 측정 파장은 일정하고 측정 속도는 달라짐
입력 : 2019.05.03 20:05
'▶ 자연과학 > ▷ 일반물리학' 카테고리의 다른 글
| 【물리학】 광학 1강. 기하광학 (0) | 2016.06.26 |
|---|---|
| 【물리학】 파동역학 3강. 파동방정식 (0) | 2016.06.26 |
| 【물리학】 파동역학 4강. 음파 (0) | 2016.06.26 |
| 【물리학】 파동역학 1강. 파동 (0) | 2016.06.26 |
| 【물리학】 역학 8강. 단진동과 진동학 (0) | 2016.06.26 |




최근댓글