파동역학 1강. 파동(wave)
추천글 : 【물리학】 물리학 목차
1. 파동의 정의 [본문]
2. 파동의 종류 [본문]
3. 파동의 표시 [본문]
4. 파동함수 [본문]
1. 파동의 정의 [목차]
⑴ 파동(wave) : 매질(물질) 이동 없이 에너지만 전달되는 것
① 정상파는 반례로 볼 수 있음
② 열 전도는 정의에 부합하나 파동이 아님
⑵ (구별개념) 진동(vibration) : 한 장소에서 주기적으로 일어남. 파동은 다른 장소로 퍼져 나감
⑶ (구별개념) 펄스(pulse) : 교란 상태가 한 번만 지나가는 것
⑷ 파원 : 파동이 처음 발생한 곳
⑸ 매질 : 파동을 전달하는 물질
2. 파동의 종류 [목차]
⑴ 매질 유무에 따른 분류
① 탄성파 : 역학적 파동. 매질을 필요로 함
○ 외력이 변형을 일으킴 → 변형은 응력을 일으킴 → 응력은 인접한 분자의 변형을 일으킴
○ 밀도가 클수록 속력이 빠름
○ 예 : 수면파, 음파, 지진파
② 입자파 : 매질을 필요로 하지 않음
○ 전자기파 (빛) : 게이지 보존, 스칼라·벡터·텐서 관여
○ 중력파 : 게이지 보존, 스칼라·벡터·텐서 관여
○ 물질파 : 확률 진폭 밀도, 페르미온 → 스피너 (상대론적으로 대략 맞음)
⑵ 진동 방향에 따른 분류
① 종파 (예 : 지진파의 P파, 음파, 용수철 종파)
○ 정의 : 파동이 진행하는 방향과 매질이 진동하는 방향이 나란한 파동
○ 진동 방향과 에너지 전달 방향이 나란
○ 압축력이 관여
② 횡파 (예 : 지진파의 S파, 전자기파, 용수철 횡파)
○ 정의 : 파동이 진행하는 방향과 매질이 진동하는 방향이 수직인 파동
○ 진동 방향과 에너지 전달 방향이 수직
○ 정단력이 관여
③ 물결파는 횡파로 구분하기도 하지만 물 입자 특유의 원운동으로 종파 성분도 존재함
⑶ 파형에 따른 분류
① 파면 : 마루나 골과 같이 위상이 같은 점을 연결한 선이나 면
② 평면파 : 파면이 선을 이루는 것
③ 구면파 : 파면이 원을 이루는 것
3. 파동의 표시 [목차]
⑴ 마루 : 파동에서 변위가 최대가 되는 지점
⑵ 골 : 파동에서 변위가 최소가 되는 지점
⑶ 진폭 : 매질이 진동하는 최대 변위
⑷ 파장 : 위상이 같은 이웃한 두 점 사이의 거리. 즉, 골에서 골 또는 마루에서 마루까지의 거리
⑸ 주기 : 일정한 패턴이 반복되는 파동의 시간 T
⑹ 진동수 : 단위 시간당 반복되는 패턴의 수, 주기의 역수(f)
⑺ 파동의 속력
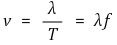
⑻ 배(antinode) : 진폭이 최대가 되는 지점
⑼ 마디(node) : 진폭이 최소가 되는 지점
⑽ 예제

Figure. 1. 파동의 파장, 진동수, 속력의 결정 예제
① (가)는 t = 0인 상황, (나)는 t = 1 s인 상황을 나타냄
② (가)를 통해 λ = 4 m임을 알 수 있음
③ (가)와 (나)를 통해 v = 1 m/s임을 알 수 있음
④ 공식을 통해 진동수를 알 수 있음
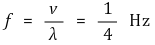
4. 파동함수 [목차]
⑴ 정의 : 진행파, 주기적 파동을 기술하기 위한 언어
⑵ 일반적 표현
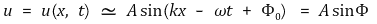
① 파수(wavenumber) :
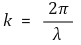
② 각진동수(angular frequency) :
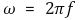
⑶ 파속 : 파동이 전파되는 속도
① 위상속도(phase velocity) : 같은 위상인 지점을 추적
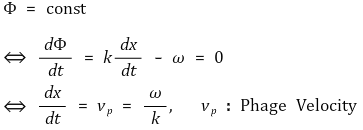
○ ω/k > 0 : vp > 0이므로 정방향 진행
○ ω/k < 0 : vp < 0이므로 역방향 진행
② 예 1. 줄파
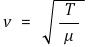
○ 증명 1. 차원분석
○ [μ] = ML-1
○ [T] = MLT-2
○ [v] = LT-1
○ [(T / μ)0.5 ] = [v] ⇔ v ∝ (T / μ)0.5
○ 증명 2. 파동방정식을 통한 유도

Figure. 2. 파동방정식을 통한 줄파의 속력 유도
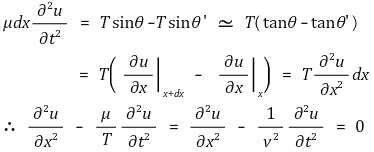
○ 증명 3. 사고실험을 통한 유도 : 구심력 공식을 활용

Figure. 3. 구심력 공식을 활용한 속력 유도
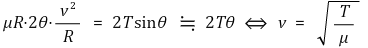
③ 예 2. 용수철 파동 : 용수철의 용수철 상수가 클수록 빠름
④ 예 3. 수면파의 속력 : 해양학에서 자세히 기술
○ 파도의 속력 일반식

○ 심해파의 속력

○ 천해파의 속력

⑤ 예 4. 소리의 속력
○ 고체 > 액체 > 기체 순으로 빠름
○ 공기의 온도가 높을수록 빠름
⑥ 예 5. 전자기파의 속력 : 진공에서 모든 전자기파의 속력은 같음
⑷ 변위 관련 물리량
① 변위속도
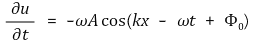
② 변위가속도
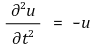
③ 곡률
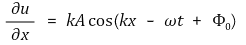
④ 기타
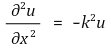
⑸ 에너지
① 진폭이 작을시 장력과 선밀도 일정
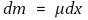
② 운동에너지 : 다음을 이용
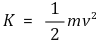
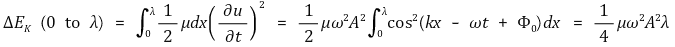
③ 위치에너지 : 다음을 이용
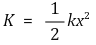
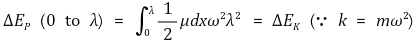
④ 전체에너지
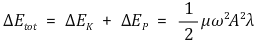
○ 탄성파는 전체에너지가 진동수의 제곱에 비례
○ 양자(quantum)는 전체에너지가 진동수에 비례. 즉, E = hf
○ 광자 또한 양자이므로 전체에너지가 진동수에 비례
⑤ 에너지 전달률
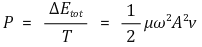
입력: 2019.05.03 17:14
'▶ 자연과학 > ▷ 일반물리학' 카테고리의 다른 글
| 【물리학】 파동역학 2강. 파동의 전파 (0) | 2016.06.26 |
|---|---|
| 【물리학】 파동역학 4강. 음파 (0) | 2016.06.26 |
| 【물리학】 유체역학 목차 (0) | 2016.06.26 |
| 【물리학】 역학 8강. 단진동과 진동학 (0) | 2016.06.26 |
| 【물리학】 역학 6강. 강체역학 (0) | 2016.06.26 |




최근댓글