역학 6강. 강체역학(회전역학, geostatics)
추천글 : 【물리학】 물리학 목차
1. 회전운동계 [본문]
2. 등속 원운동 [본문]
3. 부등속 원운동 [본문]
4. 도구와 돌림힘 [본문]
b. 관성모멘트 실험
1. 회전운동계 [목차]
| 물리량 | 의미 | 단위 | 수식 |
| 주기 T | 원운동을 1회전 하는 시간 | s | |
| 진동수 f | 단위 시간당 회전수 | Hz | |
| 각변위 θ | 회전한 각도의 양 | rad | |
| 각속도 ω | 단위 시간당 각변위의 변화량 | rad/s | |
| 선속도 v | 원운동하는 물체의 속도 | m/s | |
| 각가속도 α | 단위 시간당 각속도의 변화량 | rad/s2 | |
| 선가속도 a | 원운동하는 물체의 접선가속도 | m/s |
Table. 1. 회전운동계의 주요 물리량
⑴ 각속도 ω : 단위 시간당 각변위의 변화량
① 각속도는 반시계 방향일 때 양의 값을 가지는 것으로 정의
② 병진운동계의 속도 v와 대응되는 개념
⑵ 각가속도 α : 단위 시간당 각속도의 변화량
① 각가속도는 반시계 방향일 때 양의 값을 가지는 것으로 정의
② 병진운동계의 가속도 a와 대응되는 개념
2. 등속 원운동 [목차]
⑴ 구심가속도와 접선가속도
① 구심가속도(centripetal acceleration) : 가속도 운동인 등속 원운동의 중심방향 가속도
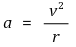
○ (참고) 등속 원운동은 운동방향이 시시각각 변하기 때문에 가속도 운동임
○ 유도 1. 호도그래프(hodograph)를 이용한 유도

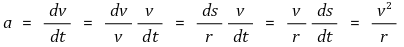
○ 유도 2. 차원분석을 이용한 유도
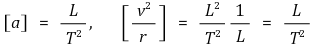
○ 유도 3. 좌표계 해석을 이용한 유도
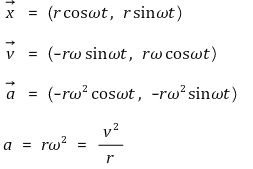
② 접선가속도(tangential acceleration) : 접선방향 가속도
○ 등속 원운동에서는 항상 0임
○ α로 표시함
⑵ 구심력(centrifugal force)
① 정의 : 구심가속도 × 물체의 질량
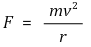
② 물체의 운동 방향에 수직하게 작용하므로 물체의 에너지가 증가하지 않음
③ 원심력
○ 정의 : 물체와 동일하게 회전하는 관찰자에 의한 가속도계에서 방사방향으로 작용하는 가상적인 힘
○ 동일한 속력으로 원운동하는 관찰자 입장 : 물체는 정지한 것처럼 보임. 구심력과 원심력이 힘의 평형 관계
3. 부등속 원운동 [목차]
⑴ 개요
① 정의 : 원운동에서 물체에 작용하는 알짜 힘이 물체 운동 방향에 수직하지 않은 경우
② 주기, 각속력 등이 일정하게 관찰되지 않음
⑵ 부등속 원운동 이론
① 단일 질점의 부등속 원운동
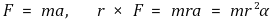
② 다중 질점의 부등속 원운동
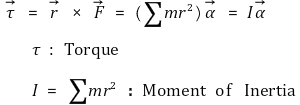
○ r 벡터 : 회전중심에서 해당 질점까지의 거리 벡터
○ τ의 방향 : 네 손가락을 작은 각도로 r 벡터에서 F 벡터로 감아쥘 때 엄지손가락이 향하는 방향
⑶ 회전관성(관성모멘트, moment of inertia)
① 정의 : 개별 질량(mi)과 회전축으로부터 떨어진 거리(ri)의 제곱을 곱하여 합한 값 Σmi ri2 (단위 : kg·㎡)
② 통계학에서 다루는 분산(variance) 혹은 적률(moment)과 굉장히 유사한 개념
③ 여러 물체의 회전관성
| 물체의 종류 | 관성모멘트 |
| 반지름이 R, 회전축이 중심인 고리 | |
| 반지름이 R, 회전축이 중심인 원판 | |
| 내경이 R1, 외경이 R2, 회전축이 중심인 실린더 | |
| 반지름이 R, 회전축이 중심인 실린더 | |
| 길이가 L, 회전축이 중심이고 길이방향에 수직인 얇은 막대 | |
| 길이가 L, 회전축이 한쪽 끝이고 길이방향에 수직인 얇은 막대 | |
| 반지름이 R, 회전축이 중심인 구껍질 | |
| 반지름이 R, 회전축이 중심은 꽉찬 구 |
Table. 2. 여러 물체의 회전관성
④ 평행축 정리 : 회전 중심이 질량 중심에 있지 않은 경우 회전관성을 계산하는 공식
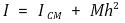
○ ICM : 질량 중심에서의 회전관성
○ M : 전체 질량
○ h : 회전축과 질량중심 사이 거리
⑷ 등각가속도 운동 공식
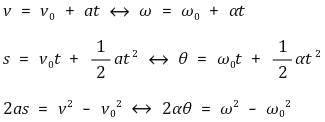
⑸ 토크(torque)
① 정의 : 강체의 각속력을 변화시키는 원인
② 병진운동계의 힘 F와 대응되는 개념
③ 수식화
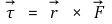
⑹ 각운동량(angular momentum)
① 수식화
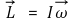
② 각운동량은 반시계 방향일 때 양의 값을 가지는 것으로 정의
③ 각운동량은 병진운동계의 운동량 p = mv와 대응되는 개념
④ 각운동량 보존의 법칙
○ 뇌터의 정리 : 대칭성이 있으면 그에 상응하는 보존량이 있어야 한다는 법칙
○ 우주는 공간에 대한 회전대칭성이 있음
○ 상응하는 보존량이 각운동량인 것으로 여겨지고 있음
⑺ 회전운동에너지
① 수식화
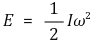
② 회전운동에너지는 병진운동계의 병진운동에너지와 대응되는 개념
③ 물체가 병진운동과 회전운동을 동시에 하는 경우 운동에너지는 병진운동에너지와 회전운동에너지의 합으로 표현
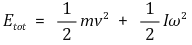
⑻ 자이로 효과
① 정의 : 빠르게 회전하고 있으면 흔들리지 않음
② 원리 : 각운동량
③ 예시 : 자전거 타기
4. 도구와 돌림힘 [목차]
⑴ 지레
① 정의 : 막대에서 받침점, 작용점, 힘점을 설정하여 힘의 이득을 보는 도구
○ 받침점 : 받침대로 막대를 받친 점
○ 작용점 : 지레가 물체에 힘을 가지는 점
○ 힘점 : 지레에 힘이 작용하는 점
② 지레의 원리

③ 지레의 종류
○ 1종 지레 : 받침점의 양쪽에 작용점과 힘점이 있는 지레
○ 예 : 가위, 펜치, 대저울, 시소 등
○ 2종 지레 : 힘점과 받침점 사이에 작용점이 있는 지레
○ 예 : 병따개, 손수레, 손톱깎이 등
○ 3종 지레 : 작용점과 받침점 사이에 힘점이 있는 지레
○ 예 : 핀셋, 낚싯대, 젓가락 등
⑵ 축바퀴
① 정의 : 지름이 다른 두 원형 바퀴를 회전축이 일정하도록 붙여서 함께 회전하도록 만든 장치
② 축바퀴의 원리 : 지레의 원리와 동일
③ 축바퀴의 종류
○ 고정도르래 : 물체를 일정 속력으로 들어올릴 때 물체의 무게와 같은 힘으로 물체를 들어올릴 수 있음
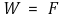
○ 움직도르래 : 물체를 일정 속력으로 들어올릴 때 2종 지레와 같음
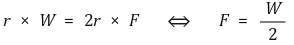
④ 예 : 자동차 운전대, 드라이버, 자전거의 기어 등
⑶ 일의 원리 : 도구를 사용하여 일을 하는 경우, 힘의 이득을 보더라도 이동거리에서 손해를 보기 때문에 한 일의 양은 변화 없음
입력: 2019.03.28 19:55
'▶ 자연과학 > ▷ 일반물리학' 카테고리의 다른 글
| 【물리학】 유체역학 목차 (0) | 2016.06.26 |
|---|---|
| 【물리학】 역학 8강. 단진동과 진동학 (0) | 2016.06.26 |
| 【물리학】 역학 5강. 운동량 (0) | 2016.06.26 |
| 【물리학】 역학 4강. 일과 에너지 (0) | 2016.06.26 |
| 【물리학】 역학 3강. 운동의 법칙 (3) | 2016.06.26 |




최근댓글