역학 4강. 일과 에너지
추천글 : 【물리학】 물리학 목차
1. 일의 정의 [본문]
2. 에너지 [본문]
3. 운동에너지 [본문]
4. 중력에 의한 위치에너지 [본문]
5. 탄성력에 의한 위치에너지 [본문]
6. 만유인력에 의한 위치에너지 [본문]
7. 일률 [본문]
1. 일의 정의 [목차]
⑴ 일 : 가한 힘의 크기 × 가한 힘의 방향으로 움직인 거리
⑵ 단위 : N·m = kg·m2 / s2 = J
2. 에너지 [목차]
⑴ 일을 할 수 있는 원동력
⑵ 역학적 에너지(E) = 위치 에너지(EP) + 운동에너지(EK)
⑶ 역학적 에너지 보존의 법칙 : 비보존력(예 : 마찰력, 공기 저항력)이 작용하지 않고 보존력만 가해지면 역학적 에너지는 처음과 나중의 값이 일정하게 보존
⑷ 에너지 보존의 법칙
① 줄의 일-열 등가성을 통해 열에너지도 역학적 에너지와 크게 다르지 않음이 밝혀짐
② 뇌터의 정리
○ 내용 : 대칭성이 있으면 그에 상응하는 보존량이 있어야 한다는 법칙
○ 우주는 시간에 대한 대칭성이 있음
○ 상응하는 보존량이 에너지인 것으로 여겨지고 있음
3. 운동에너지 [목차]
⑴ 운동 법칙에서 2as = v2 - v02으로부터 as = 0.5v2 - 0.5v02로 정리하고 질량(m)을 곱하면 mas = 0.5mv2 - 0.5mv02
⑵ 따라서 F = ma이므로 일의 변화량이 0.5 mv2 - 0.5mv02이므로 v0 = 0이라면 운동에너지는 0.5 mv2
4. 중력에 의한 위치에너지 [목차]
⑴ 중력의 크기는 mg이고 이동거리가 h이므로 이동하는 동안 중력에 의한 위치에너지는 mgh
⑵ 위치에너지는 상대적인 값으로 기준점에 따라 같은 위치에서도 서로 다를 수 있음
5. 탄성력에 의한 위치에너지 [목차]
⑴ 탄성력은 길이가 변하면서 일정하지 않고 길이 변화량에 비례하기 때문에 원래 위치에서 x만큼 늘어나는 동안 평균적으로 작용한 탄성력은 0.5 kx
⑵ 따라서 x에 탄성력에 의한 위치에너지는 0.5 kx × x = 0.5 kx2
① 적분하면 됨
6. 만유인력에 의한 위치에너지 [목차]
⑴ 중심으로부터 R인 위치의 만유인력에 의한 위치에너지
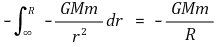
7. 일률 [목차]
⑴ 단위 시간당 일 P = W/t
⑵ 단위 : N·m/s = W
⑶ P = W / t = F · S / t = F · v
입력 : 2016.06.26 21:05
'▶ 자연과학 > ▷ 일반물리학' 카테고리의 다른 글
| 【물리학】 역학 6강. 강체역학 (0) | 2016.06.26 |
|---|---|
| 【물리학】 역학 5강. 운동량 (0) | 2016.06.26 |
| 【물리학】 역학 3강. 운동의 법칙 (3) | 2016.06.26 |
| 【물리학】 역학 1강. 벡터와 스칼라 (0) | 2016.06.26 |
| 【물리학】 역학 2강. 운동학 (0) | 2016.06.26 |




최근댓글