역학 1강. 벡터와 스칼라
추천글 : 【물리학】 물리학 목차
1. 물리량의 표현 : 스칼라 [본문]
2. 물리량의 표현 : 벡터 [본문]
3. 물리량의 표현 : 텐서 [본문]
4. 뉴턴역학의 다양한 접근 [본문]
a. 유기화학과 벡터의 외적
1. 물리량의 표현 : 스칼라(scala) [목차]
⑴ 정의 : 크기만을 갖는 물리량
① 어원 : '계단' 또는 '사다리'를 뜻하는 라틴어 scalae → scalaris → scala
② 예 : 시간, 길이, 넓이, 부피, 속력, 질량, 온도, 일, 에너지
⑵ 사칙연산이 자유로움
2. 물리량의 표현 : 벡터(velocity) [목차]
⑴ 정의 : 방향과 크기를 갖는 물리량
① 어원 : '나르다'라는 의미의 라틴어 vehere → vectus → vector
② 예 : 힘, 변위, 속도, 운동량, 충격량, 전기장, 자기장
⑵ 벡터의 표시
① 화살표로 나타내는 경우 : 화살표의 길이는 벡터의 크기를 나타냄. 화살표의 방향은 벡터의 방향을 나타냄
② 기호로 나타내는 경우
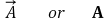
③ 절댓값 기호
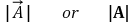
⑶ 연산 1. 벡터의 덧셈
① 방법 : 평행사변형법, 삼각형법
② 특징 1. 교환법칙
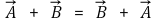
③ 특징 2. 결합법칙

⑷ 연산 2. 벡터의 뺄셈
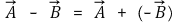
⑸ 연산 3. 벡터와 스칼라의 곱
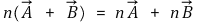
⑹ 연산 4. 벡터의 성분 분해
① 정의 : 각 벡터를 직교좌표 방향의 각 성분 벡터로 분해하는 것
② 수식화
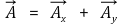
⑺ 연산 5. 스칼라곱(내적, scalar product, dot product)
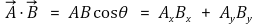
⑻ 연산 6. 벡터곱(외적, vector product, cross product)
① 외적의 정의 : v, w ∈ ℝn에 대하여 다음 3가지 연산을 만족하는 연산을 의미
○ v × w는 순서쌍 (v, w)의 연속함수
○ v × w는 v 및 w와 수직함 : (v × w) · v = (v × w) · w = 0
○ v와 w가 선형독립이면 v × w ≠ 0
② 외적의 방향 : right-hand rule을 따름
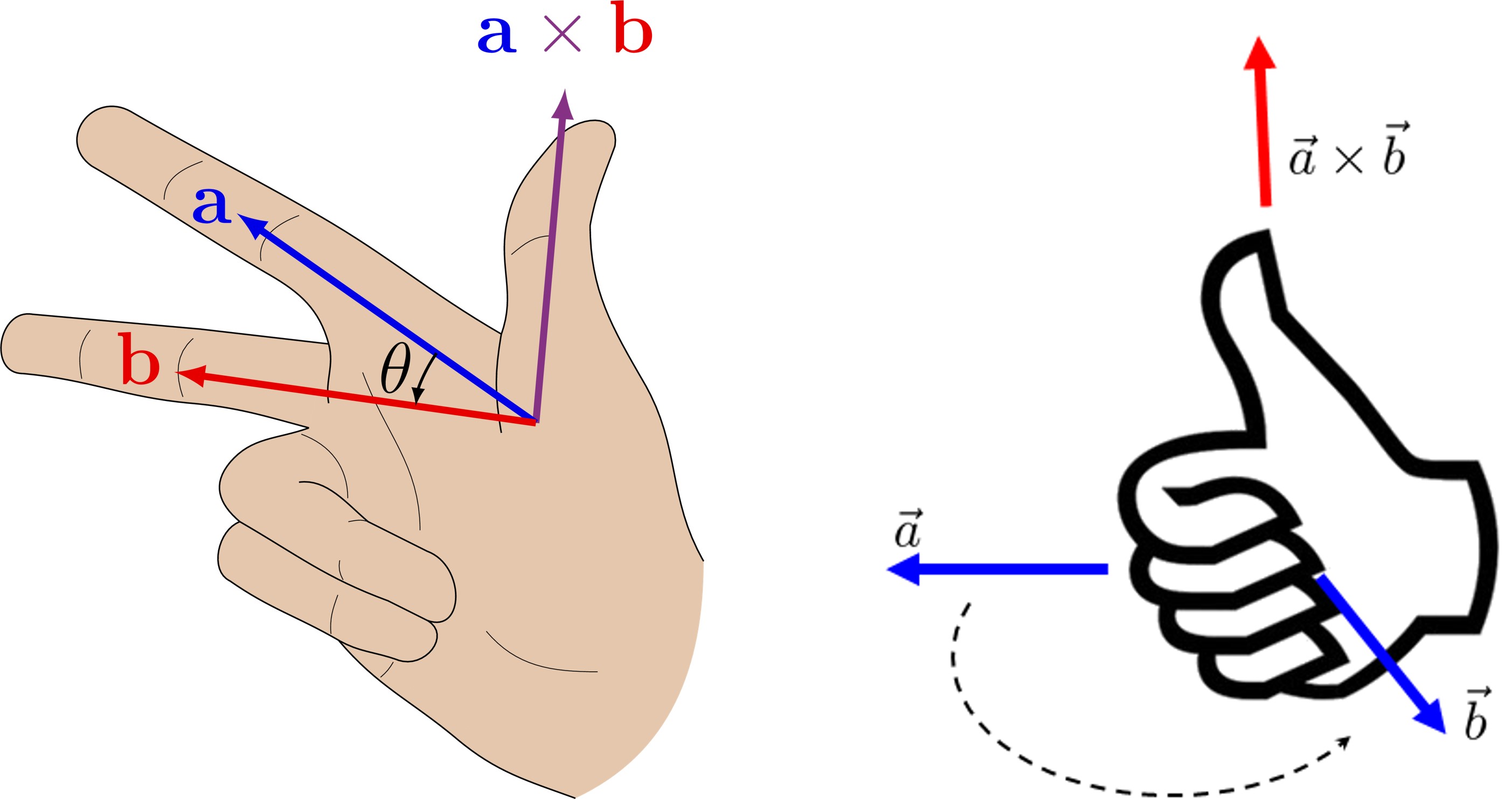
Figure. 1. 외적의 방향
③ 3차원 벡터
○ 단위 벡터의 벡터곱 : (주석) i → j → k 순으로 연산을 하면 마이너스 부호가 붙지 않음
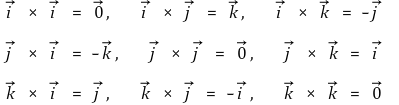
○ 기본 수식 : 단위 벡터의 벡터곱을 이용하면 증명할 수 있음
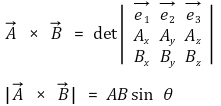
○ 벡터곱의 방향 : A에서 B로 오른손을 감아쥘 때 엄지손가락의 방향
○ 교환법칙이 성립하지 않음
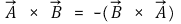
○ 평행육면체의 부피 : 벡터 a, 벡터 b, 벡터 c가 만드는 평행육면체의 부피는 다음과 같음

○ 백캡룰(BAC-CAB rule)
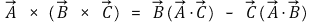
○ 증명 1. 단순 수식 전개
Figure. 1. 백캡룰 증명
○ 증명 2. 어떤 상황에서 백캡룰이 성립하고, 크기 변환 및 좌표계 회전 변환에 대해 식의 성립 여부가 보존되므로 수학적 귀납법에 의해 백캡룰이 항상 성립함 (필자의 제안 원리)
○ 어떤 상황 : A = (1, 0, 0), B = (p, q, 0), C = (t, 0, s)에서 백캡룰의 성립 여부를 쉽게 보일 수 있음
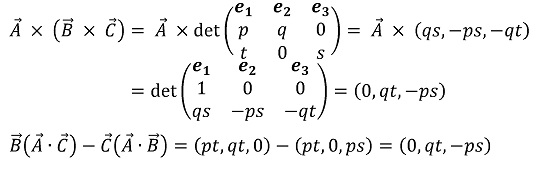
○ 크기 변환에 대해 백캡룰 성립 여부의 보존은 내적 및 외적 연산이 각 벡터의 크기에 1차 비례함으로부터 자명하게 도출
○ (B × C) 및 A × (B × C)의 방향이 좌표계 회전에 대해 A, B, C와 동일하게 변하므로 백캡룰 성립 여부는 최종 증명됨
④ 다차원 벡터에서의 외적의 정의
○ 외적을 정의할 수 있는 것은 3차원 또는 7차원에 한함 (ref)
3. 물리량의 표현 : 텐서(tensor) [목차]
⑴ 응용 1. 유체역학 미분형 방정식
⑵ 응용 2. 일반 상대성 이론
4. 뉴턴역학의 다양한 접근 [목차]
⑴ 뉴턴(Newtonian) 해석
① 힘과 가속도 등의 벡터량을 통해 역학적인 분석을 하는 것
⑵ 라그랑지안(Lagrangian) 해석
① 에너지 등의 스칼라량을 통해 역학적인 분석을 하는 것
② L (Lagrangian) = T (kinetic energy) - U (potential energy)
⑶ 해밀턴(Hamiltonian) 해석
① 해밀턴 H = Σ pi qi' - L
○ pi : generalized momenta
○ qi : generalized coordinate
② 단일 입자만 있는 단일 시스템에서는 H (Hamiltonian) = T (kinetic energy) + U (potential energy)로 표현할 수 있음
③ 양자역학에서의 해밀턴
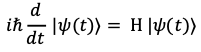
⑷ 에르미트(Hermitian) 해석
① 양자역학에서의 에르미트
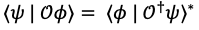
② Hamiltonian은 항상 Hermitian operator에 해당함
입력: 2016.06.26 21:05
수정: 2023.10.07 21:55
'▶ 자연과학 > ▷ 일반물리학' 카테고리의 다른 글
| 【물리학】 역학 4강. 일과 에너지 (0) | 2016.06.26 |
|---|---|
| 【물리학】 역학 3강. 운동의 법칙 (3) | 2016.06.26 |
| 【물리학】 역학 2강. 운동학 (0) | 2016.06.26 |
| 【물리학】 2012 MEET/DEET 물리학 (0) | 2016.06.26 |
| 【물리학】 빅뱅이론에서 나온 현대물리학 퀴즈들 (0) | 2016.06.25 |





최근댓글