현대물리학 2강. 상대성이론
추천글 : 【물리학】 물리학 목차
1. 뉴턴 패러다임 [본문]
2. 상대성 원리 [본문]
3. 갈릴레이 상대론 [본문]
4. 특수 상대성이론 [본문]
5. 일반 상대성이론 [본문]
1. 뉴턴 패러다임(Newtonian paradigm) [목차]
⑴ 뉴턴의 1, 2, 3법칙은 거리, 시간, 힘, 에너지의 관계를 기술
① 뉴턴이 정의한 시간
Absolute, true and mathematical time, of itself, and by its own nature, flows uniformly on, without regard to anythiing external.
② (참고) 아인슈타인이 정의한 시간
Time is the fourth dimension.
⑵ 뉴턴 패러다임
① 모든 현상을 뉴턴 법칙으로 해석할 수 있다는 믿음
② 기계론적 세계관
③ (참고) 라플라스의 악마, 괴물, 마녀, 도깨비
⑶ 1800년대 말 뉴턴역학으로 도저히 설명할 수 없는 현상이 대두됨
① 양자역학의 도입 : 굉장히 작은 스케일(ℓ ≪ 1)에서는 뉴턴역학을 적용할 수 없음
② 상대성이론의 도입 : 굉장히 큰 스케일(v ≫ 1)에서는 뉴턴역학을 적용할 수 없음
2. 상대성 원리 [목차]
⑴ 상대성 원리(principle of relativity)
① 상대성 원리 1. 물리량은 좌표계에 따라 달라질 수는 있음 (상대성)
② 상대성 원리 2. 물리법칙 자체는 좌표계에 따라 변하지 않음 (절대성)
⑵ 상대성 이론(theory of relativity)
① 정의 : 상대성 원리를 구체적인 좌표계 변환이론에 적용한 것
② 이론 1. 갈릴레이 상대성이론
○ 원리 : 상대성 원리
○ 좌표계 변환 : 벡터 덧셈
○ 좌표공간 : 유클리드 공간
○ 조건 : 관성계, v ≪ c
○ 관련 이론 : 뉴턴 역학
③ 이론 2. 특수 상대성이론
○ 원리 : 상대성 원리, 광속불변의 원리
○ 좌표계 변환 : 로렌츠 변환 (4벡터 일차변환)
○ 좌표공간 : 민코프스키 공간
○ 조건 : 관성계, GM / r = Φ ≪ c2
○ 관련 이론 : 맥스웰 전자기학
④ 이론 3. 일반 상대성이론
○ 원리 : 상대성 원리, 등가원리, 마하의 원리
○ 좌표계 변환 : 메트릭 변환 (2계 텐선 변환)
○ 좌표공간 : 리만 공간
○ 조건 : 비관성계, 미적분 가능, h → 0 (즉, 양자역학 무시)
○ 관련 이론 : 우주론
3. 갈릴레이 상대론 [목차]
⑴ 특징
① 우리에게 굉장히 친숙한 개념
② 속도의 덧셈법칙이 성립합
③ 관성계 : 가속도가 0인 계
⑵ 좌표계 변환
① 관찰자 X가 (0, 0, 0)에서 출발하여 (u, 0, 0)의 속도로 운동한다고 하자.
② 어떤 지점 P(x, 0, 0)가 있다고 하자.
③ 운동하지 않는 관찰자 Y가 보기에는 P는 여전히 (x, 0, 0)이다.
④ 관찰자 X는 최초에 P를 (x, 0, 0) 지점에 있는 좌표로 인식했다.
⑤ t 만큼 운동하자 관찰자 X는 P를 (x - ut, 0, 0) 지점에 있는 좌표로 인식한다.
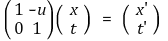
⑶ 뉴턴역학은 상대성 원리를 만족
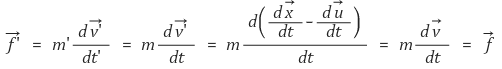
⑷ 관성계와 가속계
① 관성좌표계(관성계) : 정지 또는 등속 직선 운동을 하는 관찰자를 기준으로 정한 좌표계
② 가속좌표계(가속도계) : 가속도 운동을 하는 관찰자를 기준으로 정한 좌표계
③ 구별의 실익 : 관성계는 관성력이 나타나지 않음. 가속계는 관성력이 나타남
○ 위로 a만큼 가속하는 엘리베이터와 같이 운동하는 관찰자 : 관찰자는 아래로 ma만큼의 관성력을 관찰함
○ 아래로 a만큼 가속하는 엘리베이터와 같이 운동하는 관찰자 : 관찰자는 위로 ma만큼의 관성력을 관찰함
○ 원운동하는 계와 같이 운동하는 관찰자 : 관찰자는
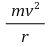
만큼의 원심력이라는 관성력을 관찰함
④ 관찰자가 받는 가속도는 관성력이 있다는 점에서 상대적이지 않음
⑸ 광속의 유한성
① 증거 1. 목성의 식(eclipse)
○ Giovanni Cassini (1625-1712)
○ 지구가 목성으로 근접 시 eclipse time이 짧아짐
○ 지구가 목성에서 멀어질 경우 eclipse time이 길어짐
○ Røemer의 논증
○ eclipse time의 차이는 빛의 이동시간의 차이라고 추론함
○ 빛의 속도는 유한하다는 결론을 이끌어 냄
② 증거 2. 톱니 실험 : 실제로는 톱니가 매우 빨라야 반사된 빛이 톱니에 가려지지 않음
4. 특수 상대성이론(special theory of relativity) [목차]
⑴ 아인슈타인의 발상
① 1st. 1870년 즈음 전신이 쓰이기 시작
② 2nd. 기차의 경우 출발시간과 도착시간을 알려주어야 하므로 시계를 동기화하는 방법 필요
③ 3rd. 당시 서로 다른 지역의 두 시계를 동기화하는 방법이 없었음
④ 4th. 스위스 특허청에 시계를 동기화하는 방법에 대한 특허가 많이 들어옴
⑤ 5th. 아인슈타인은 당시에 스위스 특허청에서 근무
⑥ 6th. 아인슈타인이 당장의 시간을 알려고 시계를 보는 순간 그 신호가 자기한테 도달하는 데 시간이 더 경과함을 착안
⑦ 7th. 즉, 아인슈타인은 손목시계와 생체시계가 같은 시간을 나타낼 수 없음을 깨달음
⑧ 8th. 더 나아가 아인슈타인은 시간이 절대적이지 않다고 생각
⑵ 광속불변의 법칙
① 맥스웰 방정식(Maxwell equation)
○ 맥스웰은 전기 현상이 전자기파의 파동방정식으로 기술된다는 것을 발견
○ 전자기파의 속도가 기존에 알려진 광속(3 × 108 m/s)과 비슷한 값을 발견
○ 빛 = 전자기파라는 중요한 발견을 함
② 에테르 이론(ether theory)
○ 모든 파동은 파동을 전달하는 매질이 있음
○ 빛은 전자기파이므로 매질이 있을 것이고, 이 매질을 에테르(ether)라고 명명
○ 빛이 에테르 속에서 움직일 때 빛의 속도는 에테르의 속도에 따라 달라짐

③ 아인슈타인의 발상
○ 전기 현상은 움직이는 계에서든 정지한 계에서든 잘만 일어남
○ 전기 현상은 정확하게 3 × 108 m/s의 속력을 갖는 전자기파가 있어야 일어날 수 있음 (∵ 맥스웰 방정식)
○ 움직이는 계에서도 전기 현상이 일어남
○ 따라서 빛의 속력은 일정
④ 증거 : 마이켈슨-몰리(Michelson-Morley) 간섭실험

○ 마이켈슨 간섭계는 간섭무늬의 이동을 볼 수 있을 만큼 정밀한 기계
○ 50년간 마이켈슨-몰리 실험의 정밀도를 높여 옴
○ Michelson, Studies in Optics (1881)
○ Shankland, et al., Rev. Mod. Phys. 27, 167 (1955)
○ 동일하게 출발한 빛이라도 반거울에서 출발한 뒤 다시 도착할 때 시간차가 생김
○ 에테르의 속도를 v = (vx, vy)라고 가정
○ 시간차 계산
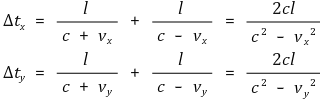
○ 결과 1. 마이켈슨-몰리 간섭장치를 회전시킬 때 간섭 무늬의 이동이 없으므로 에테르 이론은 틀림
○ 예 : 시간차가 파동 하나 더 들어갈 정도의 시간이면 보강간섭이 일어남
○ 결과 2. 에테르 이론이 틀리므로 광속은 일정
○ 마이켈슨과 몰리는 실험의 정밀도가 낮아서 에테르의 속도를 측정할 수 없다고 결론을 내림
○ (주석) 결과의 부존재를 가지고 노벨상을 받은 유일한(?) 사례
⑶ 특수 상대성 이론
① 아인슈타인은 1905년 만 26세의 나이로 첫 논문을 발표
○ 첫 논문 : 움직이는 물체의 전기역학에 관하여 (On the Electrodynamics of Moving Bodies)
② 가정
○ 가정 1. 물리법칙은 어느 관성계에서나 동일 (맥스웰 방정식 포함)
○ 가정 2. 진공에서 빛의 속도는 어느 관성계에서나 동일
○ 가정 3. 관찰자의 좌표계는 관찰대상에 대하여 관성계여야 함 : 특수하다는 것의 의미
③ 응용 1. 사건의 동시성, 이시성 (simultaneity and heterochrony of events)
○ 동시에 일어난 사건일지라도 관찰자의 운동 상태에 따라 달리 보임

○ A가 볼 때 P와 R에서 방출된 빛이 Q에 동시에 도달하는 경우 B가 볼 때에도 두 빛이 Q에 동시에 도달함
○ 사건의 동시성의 상대성은 서로 다른 사건의 선후관계를 다르게 볼 수 있다는 의미
○ 그렇다고 하여 하나의 사건의 사실관계를 다르게 볼 수 있다는 것은 아님

④ 응용 2. 상대속도(relative velocity)
○ 상황 : A와 B가 등속도로 움직이고 있음
○ 결론 : A가 B를 보았을 때의 상대속도의 크기와 B가 A를 보았을 때의 상대속도의 크기는 같음
○ 대단히 중요한 개념
⑤ 응용 3. 시간팽창(시간지연, time dilation)

○ 사건 : 빛이 초기 지점에서 출발하여 거울에서 반사된 뒤 초기 지점으로 다시 돌아오는 것
○ 우주선 내 관찰자가 측정한 시간 Δt0
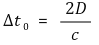
○ 지상의 관찰자가 측정한 시간 Δt
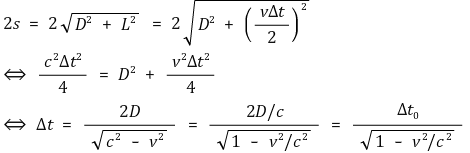
○ 요약 : 관찰자가 움직이는 물체를 보면 그 물체가 느리게 움직이는 것처럼 보임
○ 예 1. 성층권에서 생성된 뮤온은 정지시 2.2 × 10-6초의 수명을 가짐
○ 예 2. 성층권 내에서 v = 0.999 c이므로 1.1 × 10-3 초의 수명을 가짐
⑥ 응용 4. 길이수축(length contraction)


○ 사고실험 : 상대속도 v는 우주선 내 관찰자와 지상의 관찰자가 같음
○ 길이수축 유도 : 상대속도가 일정함을 이용
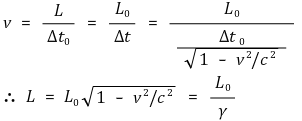
○ Δt : 관찰자가 속한 좌표계에서 측정한 운동하는 상대방의 이동시간. 시간이 지연된 상태로 측정됨
○ L0 : 관찰자가 속한 좌표계에서 측정한 두 점 P, Q의 거리
○ Δt0 : 운동하는 상대방이 속한 좌표계에서 측정한 그 관찰자의 이동시간
○ L : 운동하는 상대방이 속한 좌표계에서 측정한 두 점 P, Q의 거리
○ 시간은 운동하는 상대방의 관점에서 중요하므로 운동하는 상대방이 측정한 시간이 고유시간이 됨
○ P-Q 사이의 거리는 관찰자가 속한 좌표계에서 중요하므로 관찰자가 측정한 거리가 고유거리가 됨
○ 관찰자와 상대방에 대하여 상대방이 P 또는 Q에 있는 사건은 동시성이 없음
○ 즉, 상대방이 Q에 도달하더라도 관찰자는 도달하지 않은 것처럼 보임
Δt > Δt0
○ (주석) 각 기호가 나타내는 의미를 제대로 파악하는 게 중요함
○ (주석) 개인적으로 상대성이론의 취지를 생각하면 특정 당사자가 측정한 물리량이 고유물리량이라고 부적절함
○ 요약 : 관찰자가 움직이는 물체를 보면 그 물체는 짧아진 것처럼 보임
○ 예 1. 뮤온의 입장에서 2.2 × 10-6초 내에 성층권에서 지구 표면까지 가려면 그 거리가 단축돼야 함
⑷ 로렌츠 좌표 변환(Lorentz coordinate conversion)
① γ factor : 1보다 큼. γ > 0.9 c가 되면 γ는 급격히 증가
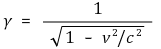
② 로렌츠 변환 유도

Figure. 7. 로렌츠 변환 유도 모델
○ 상황
○ 원점에서 빛이 발사되어 t 만큼의 시간이 흐른 뒤에 빛이 (x, y, z)에 도달
○ 원점에서 정지한 S 관찰자는 그 빛이 t 만큼의 시간이 흘렀을 때 (x, y, z)에 도달한 것으로 관찰
○ 원점에서 출발한 S' 관찰자는 그 빛이 t 만큼의 시간이 흘렀을 때 (x', y', z')에 도달한 것으로 관찰
○ 추가가정 : 빛은 x축으로 발사됐다고 가정
○ 주의
○ S 관찰자와 같은 관성계에 있으면 S 관찰자는 정지한 관찰자, S' 관찰자는 움직이는 물체
○ S' 관찰자와 같은 관성계에 있으면 S 관찰자는 움직이는 물체, S' 관찰자는 정지한 관찰자
○ S'에서 (x, y, z)를 느끼는 방식은 정지한 관찰자가 움직이는 물체를 느끼는 방식과 같음
○ 광속 불변의 법칙 적용
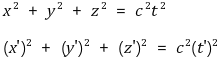
○ x' 관계식 유도 : 갈릴레이 상대론에 따르면 x'exp = x - vt, S' 관찰자에게는 x'exp가 γ배만큼 축소돼 보임 (거리 단축)
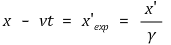
○ 광속 불변의 법칙 적용식과 x' 관계식을 융합 : S' 관찰자에게는 S 관찰자가 빛을 관찰하는 데 오래 걸린다고 생각
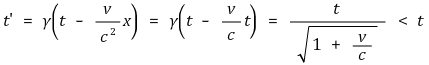
○ 수식화 : β = v / c에 대해
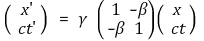
⑸ 로렌츠 속도 변환(Lorentz velocity conversion)
① 상황
○ S 좌표계에서 입자가 속도 v로 움직임
○ S'이 S에 대해 속도 u (x축 방향)로 움직임
○ S'에서 관측하는 입자의 속도는?
② 유도
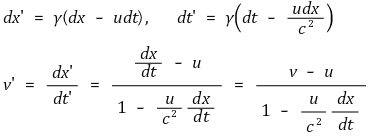
③ 결론
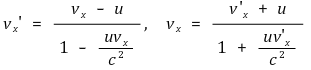
④ 상대론적 속도덧셈
○ v1으로 달리는 로켓에서 달리는 방향으로 v2의 속도로 물체를 쏜 경우 지상에서 보는 관측자에 대한 속도
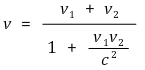
○ 근사식 : v1, v2 ≪ c라면
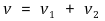
○ 서로 다른 좌표계에서 속도를 더할 수 없다는 의미이지 동일 좌표계에 대해 속도를 더할 수 있음
○ 상황 : A 좌표계에서 B, C가 각각 0.8c, 0.9c의 속도로 서로 마주보고 운동하는 경우
○ A 좌표계에서 B와 C가 가까워지는 속도 : 1.7c
○ B가 보았을 때 C의 속도 : P가 보았을 때 Q의 속도를 vPQ로 정의함

⑹ 빛의 도플러 효과
① 세로 도플러효과 : 광원이 관찰자를 향해 가까이 올 때 : 광원 자체가 오면서 파장이 짧아짐. 시간 팽창 효과
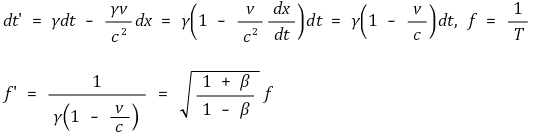
② 가로 도플러효과 : 광원이 옆으로 접근할 때
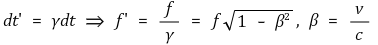
⑺ 질량-에너지 등가공식
① 상대론적 질량
○ 전자의 속도에 따라 전자의 질량이 다르게 측정됨
○ (참고) 고전역학에서 질량은 일정하게 나타남
○ 이유 : 질량은 에너지이기 때문

Figure. 8. 카우프만, 부커러, 로렌츠의 실험
(Abraham, Lorentz, Bucherer's experiment)
② 정지질량에너지
○ 발상 : 물질로부터 에너지가 방출될 때의 사고실험

Figure. 9. 아인슈타인 박스(Einstein's box)
○ 상황 : 박스의 왼쪽 끝에서 에너지가 방출 → 질량이 M인 박스가 움직임 → 에너지가 오른쪽 끝과 만남
○ (주석) 광자의 경우 질량은 없지만 광압 등 운동량이 있음을 직관적으로 알 수 있음
○ v에 관한 식 유도 : 운동량 보존식 이용. 에너지의 운동량은 광자의 경우처럼 p = E / c라고 둠
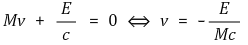
○ Δt에 관한 식 유도 : 에너지가 박스의 왼쪽 끝에서 방출되어 박스의 오른쪽 끝과 만날 때까지의 시간
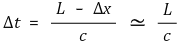
○ Δx에 관한 식 유도
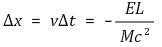
○ 에너지를 질량 m으로 환가할 수 있다고 가정 (핵심)
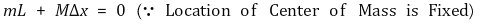
○ 결론 : E = mc2
○ 한계 1. Δt에 관한 수식이 근사식으로 돼 있음
○ 한계 2. 시간과 공간에 대한 특수 상대론적 고려를 하지 않음
○ 의의 1. 질량이 곧 에너지라는 의미를 도출할 수 있음
○ 의의 2. 에너지가 mc2에 비례할 것이라는 결론은 차원해석에 의해서도 지지됨
○ 응용 1. 광압(light pressure) 계산
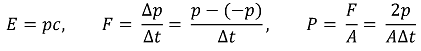
○ E : 광자의 에너지
○ p : 광자의 운동량
○ c : 빛의 속력
○ F : 면적이 A인 판에 걸리는 힘
○ Δt : 적당한 시간 구간
○ P : 광압
③ 운동에너지 : 힘 F를 주어 속도 v가 될 때까지 하는 일
○ 유도
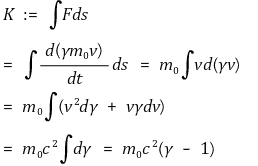
○ 참고
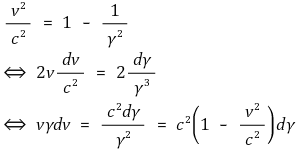
⑤ 물체의 총 에너지
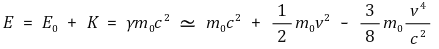
⑥ 상대론적 운동량
○ 상대론적 운동량 : p = γm0v
○ 상대론적 에너지와의 관계식 : E2 = p2c2 + (m0c2)2
○ 질량이 없는 물체(예 : 광자) : m0 = 0, E = pc
○ 정지질량 에너지 : p = 0, E = m0c2
⑦ 예 1. 원자폭탄
⑧ 예 2. 태양의 핵융합 : 아인슈타인의 이론이 나오기 전에는 태양의 에너지가 어디서 나오는지 몰랐음
⑨ 예 3. 입자 가속기에서 새로이 생성되는 새로운 입자들
⑽ 민코프스키 공간(Minkowski diagram) : 두 관성계의 시공간의 시각화
① 정지한 경우

Figure. 10. 정지한 경우 세계선도
○ 1차원의 경우를 먼저 생각
○ 수평축을 x, 수직축을 ct라고 정의
○ x = 1에서 정지해 있는 물체는 시간이 흐름에 따라 빨간선으로 표시
○ x' = 0이므로 이 빨간선이 ct' 축이 됨
② 시간축 만들기


Figure. 11. 움직이는 물체의 세계선도의 시간축 정의
○ 속도 v로 움직이는 물체는 초록색 실선으로 표시됨
○ 속도 -v로 움직이는 물체는 초록색 점선으로 표시됨
○ ct' 축이 ct 축과 이루는 각도 θ는 tan θ = v / c
○ v = -c로 움직이는 빛은 파란색으로 표시할 수 있음
○ 이때 ct' 축이 ct 축과 이루는 각도 θ는 45°
③ 공간축 만들기

Figure. 12. 움직이는 물체의 세계선도의 공간축 정의
○ x축에 있는 좌표들은 모두 t = 0임
○ 따라서 x' 축에 있는 좌표들은 모두 t' = 0임
○ ct' = 0이 되려면 ct - βx = 0, 즉 ct = βx
○ 즉, tan θ = β가 되는 직선
④ 좌표의 눈금 만들기
○ 로렌츠 변환에서 두 이벤트 (x1, y1, z1, t1)과 (x2, y2, z2, t2)의 거리를 다음과 같이 정의
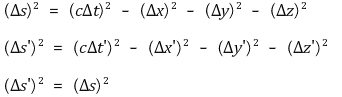
⑾ 현상 : 광속에 가깝게 달리면
① 전체가 휘어져 보이기 시작
○ 운동방향의 길이는 줄어들어 보임
○ 운동방향의 직각방향의 길이는 변함 없음
② 색깔까지 변함
○ 다가오는 별은 청색편이(blue shift), 멀어지는 별은 적색편이(red shift)
○ 도플러 효과만 고려하면 정면이 까맣게 보일 것임
○ 도플러 효과와 찌그러짐 효과를 같이 고려하면 정면이 하얗게 보임
⑿ 요약 : 상대론적 역학
① 4-벡터 : xμ ≡ (ct, x, y, z) ≡ (x0, x1, x2, x3)
② 4-속도 벡터 : uμ ≡ (γc, γv)
③ 4-운동량 : pμ ≡ muμ ≡ (γmc, γmv)
④ 로렌츠 스칼라
○ 시공거리 : |xμ|2 ≡ (ct)2 - x2 - y2 - z2 = (ct')2 - x'2 - y'2 - z'2
○ 운동량 : |pμ|2 ≡ (γmc)2 - (γmv)2 = m2c2 ⇔ (E/c)2 = m2c2 + p2
⑤ 운동방정식 : m dv / dt = f ⇔ dpμ / dτ = fμ
5. 일반 상대성이론(general theory of relativity) [목차]
⑴ 개요
① 아인슈타인은 중력이 왜 있는지를 고민
② 중력은 시공간을 휘게 만들기 때문에 질량에 영향을 줌
⑵ 핵심원리
① 상대성 원리
② 등가원리(equivalence principle) : 중력과 관성력을 구별할 수 없음

Figure. 13. 등가원리
③ 마하의 원리(Mach's principle)
○ 정의 : 우주의 전체적인 물질 분포가 국소적인 물체 운동에 영향을 준다는 원리
○ 물질분포가 공간구조를 변화시킨다는 함축이 있음
⑶ 아인슈타인의 발상
① 태양 주위를 도는 행성의 운동을 생각
② 태양의 질량이 행성의 운동에 영향을 미치므로 행성은 태양을 느끼고 있음
③ 태양은 자신의 정보를 행성에게 준다는 의미
④ 모종의 이유로 태양은 자신의 정보를 광속으로 전달
○ 질량이 0이면서 신호를 전달하는 것은 모두 광속임
⑤ 태양이 보낸 정보가 태양으로부터 r만큼 이동했으면 정보의 밀도는 다음과 같음
정보플럭스 = 정보 총량 ÷ 4πr2
⑥ 중력 또한 정보이므로 거리의 제곱에 반비례하게 됨
⑦ 중력은 상호작용이므로 두 물체의 질량의 곱을 곱하여 뉴턴의 만유인력 식을 완성하게 됨
⑷ 내용
① 1915년 아인슈타인이 발표
② 개요 : 에너지-물질 분포에 따라 시공간의 곡률이 정해지고 물체는 측지선을 따라 운동
③ 핵심 개념 1. 아인슈타인 장방정식(우주방정식)

○ 왼쪽 항은 공간, 오른쪽 항은 질량 및 에너지를 의미함
○ 왼쪽 항을 Gμv로 표시하기도 함
○ 아인슈타인은 우주가 중력수축하지 않는다는 가정을 위해 Λgμv 항을 추가함
○ 이때 Λ를 우주상수(cosmological constant)라고 함
○ 나중에 아인슈타인은 Λ를 실수로 도입했다고 시인한 바 있음
○ 그 이후 우주의 가속팽창이 밝혀지면서 Λ를 도입하는 게 타당했음이 밝혀짐
④ 핵심 개념 2. 측지선 방정식 : 직선 경로 결정
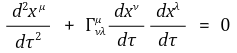
○ 0의 의미는 외력이 0이라는 의미
○ 관성운동(중력효과 포함)
⑤ 핵심 개념 3. 프리드만 방정식
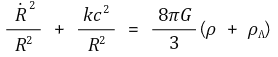
○ 아인슈타인 장방정식에 우주원리(균일, 등방)를 적용
○ FLRW 메트릭
○ Tμν = (ρ, -p, -p, -p)
⑥ 아인슈타인의 이론은 1919년 5월 29일 에딩턴(eddington)의 일식 관측에 의해 최초로 입증됨
⑸ 예 1. 쌍둥이 역설(twin paradox)
① 등장인물 : 우주여행을 한 쌍둥이 1인 A, 지구에 남아 있던 쌍둥이 1인 B
② 상황
○ A와 B가 30세일 때, A는 로켓을 타고 먼 행성에 간 뒤 지구로 귀한함
○ 로켓의 속도는 v = 0.6 c임
③ B의 관점
○ B는 정지해 있고, A가 상대적으로 운동 : A에게 시간 팽창이 일어남
○ B가 60세일 때, A는 54세 (∵ 시간지연)
④ A의 관점
○ A가 정지해 있고, B가 상대적으로 운동 : B에게 시간 팽창이 일어남
○ A가 60세일 때, B는 54세 (∵ 시간지연)
⑤ 모순 : A가 지구에 돌아왔을 때 A가 나이가 많은가, B가 나이가 많은가?
⑥ 해답 : B가 60세일 때 A가 54세임
⑦ 이유 : A는 큰 가속도를 경험했고, B는 중력가속도만 경험 → A의 시간이 느리게 흐름
⑹ 예 2. 인공위성
① 공간은 세 개의 측정지점으로부터의 거리가 주어지면 위치를 결정할 수 있음
② 인공위성에 의한 공간적 위치 결정은 시간을 담당하는 인공위성 1개를 추가로 필요로 함, 즉 4개가 필요
③ GPS 위성은 지구 중력의 영향으로 일반 상대론적 조정도 필요
④ 특수 상대론적 영향 : 시계는 7 ㎲/day만큼 느려짐
⑤ 일반 상대론적 영향 : 시계는 45 ㎲/day만큼 빨라짐

⑺ 예 3. 수성의 근일점 이동

① 뉴턴역학에 의하면 수성은 574"만큼 세차운동을 함 → 근일점 이동
② 574"는 실제 관측값과 43"만큼 차이가 남
③ 일반 상대성 이론에 의한 시공간 왜곡을 고려하면 43"을 설명할 수 있음
⑻ 예 4. 중력 렌즈 효과 : 블랙홀과 같이 중력이 큰 물체에 의해 공간이 왜곡됨

Figure. 16. 중력 렌즈 효과
① 에딩턴의 관측 결과

○ 1919년 5월 29일 개기 일식 때 태양 근처의 별들을 촬영
○ 결과 : 태양의 가까운 위치에 보이는 별일수록 별의 위치 변화가 큼
○ 결론 : 태양에 가까울수록 시공간이 크게 휘어짐
② 아인슈타인의 원과 아인슈타인의 십자가
⑼ 예 5. 중력적색이론
① 종류 1. 일반 도플러 효과에 의한 적색편이
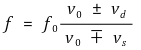
○ vs : 파원(예 : 음원)의 속력
○ vd : 관측기의 속력
○ v0 : 파동(예 : 음파)의 속력
○ f0 : 파동의 주파수
○ f : 관측 주파수
② 종류 2. 우주론적 도플러 효과에 의한 적색편이
○ 1st. 우주가 팽창
○ 2nd. 공간이 팽창함에 따라 빛의 파장이 길어짐
○ 3rd. 가시광선 파장이 적색으로 편이함
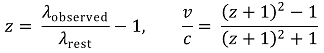
③ 종류 3. 상대론적 도플러 효과에 의한 적색편이
○ 1st. 중력은 시공간을 휘게함 → 공간을 늘어나게 하는 효과가 있음
○ 2nd. 공간이 늘어남에 따라 빛의 파장이 길어짐
○ 3rd. 가시광선 파장이 적색으로 편이함
④ 큰 별 주변에서 온 빛일수록 실제 파장보다 더 긴 빛이 관찰
⑽ 예 6. 최초의 블랙홀 관측


① 일반 상대성이론은 매우 큰 질량에 의한 공간의 휨에 의해 빛조차 빠져나올 수 없는 경우가 있다고 예측함
② 2019년 4월 10일 22:00에 최초로 블랙홀을 관측함
○ 블랙홀 관측을 하려면 지구 전체만한 망원경이 필요했음
○ 알고리즘으로 지구 각지의 망원경의 영상을 조합하는 식으로 해결
⑾ 예 7. 중력파

① 중력파 : 질량이 큰 물체가 진동할 때 공간의 휘어짐이 발생하고, 이것이 파동처럼 주변으로 퍼져 나가는 것
② 일반 상대성 이론에 따르면 중력 또한 정보를 전달하므로 정보를 전달하는 입자가 있다고 예측
③ 불과 최근까지 물리의 근본적인 네 가지 힘 중 중력을 제외하고 힘을 전달하는 게이지 보존 입자가 있다고 보고됨
④ 2015년 9월 라이고(LIGO) 관측소에서 인류 최초로 중력파를 측정하는 데 성공함
○ 2016년 2월 11일 중력파 측정에 대한 연구결과가 발표됨
○ 두 개의 큰 천체가 융합하면서 생기는 중력의 요동을 측정함
입력: 2019.04.16 00:09
'▶ 자연과학 > ▷ 일반물리학' 카테고리의 다른 글
| 【물리학】 광학 3강. 양자광학 1부 (0) | 2020.03.25 |
|---|---|
| 【물리학】 물리학 목차 (0) | 2020.01.12 |
| 【물리학】 물리학 실험 목차 (0) | 2019.07.11 |
| 【물리학 실험】 7강. 등전위선 실험 (7) | 2019.06.29 |
| 【물리학 실험】 6강. 옴의 법칙 실험 (2) | 2019.06.29 |




최근댓글