6강. 옴의 법칙 실험
추천글 : 【물리학 실험】 물리학 실험 목차
1. 실험의 목적 [본문]
2. 이론적 배경 [본문]
3. 실험장치 및 방법 [본문]
4. 실험결과 [본문]
5. 실험결론 및 논의 [본문]
a. 저항
1. 목적 [목차]
물리학은 중력, 전자기력, 강력, 약력에 의해 지배된다. 이 중 핵자간 힘인 강력과 약력은 거시세계에서 나타나기 어렵고, 중력은 유체역학에서 알 수 있듯이 이용하기 어려운 힘이다. 반면 전자기력은 예상하기 쉽고 확장성이 있어 일찍이 인류의 삶을 상당히 개선시켰다. 전자기력은 특히 회로이론으로 대표되고 회로이론의 핵심적인 개념은 옴의 법칙이다. 본 실험을 통해 옴의 법칙을 확인하고 보정하는 방법을 배울 수 있다.
2. 이론적 배경 [목차]
2.1. 옴의 법칙 유도
전자의 질량 m, 전하량 q, 충돌빈도수 μ에 대해 운동방정식은 다음과 같다.

이를 적분하면 다음과 같다.

t = 0일 때 v = 0이므로 다음과 같다.

전류밀도를 J, 전기전도도를 σ라고 하자.

도선의 재료로 많이 사용하는 구리의 경우 시간상수 τ = 1 / μ = 10-14이므로 e-μt 항이 무시될 수 있어 다음과 같이 간주해도 무방하다.
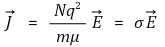
옴물질에서 다음이 근사적으로 성립한다.
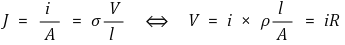
2.2. 옴물질, 비옴물질
전류나 전압이 변해도 저항이 변하지 않는 물질을 옴물질이라고 정의한다. 사실 모든 물질은 비옴물질이며, 옴물질은 좁은 구간에서만 유효한 개념이다. 도체, 부도체는 온도가 증가함에 따라 원자 진동이 증가한다. 그 결과 충돌빈도수 μ가 증가하고 σ가 감소하여 저항이 증가한다. 다음은 일반적인 저항의 온도-저항 관계를 나타내고 있다.
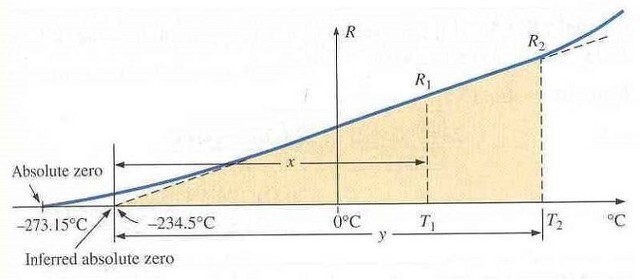
외삽 온도인 Ti (Inferred Absolute Zero), 20 ℃저항값 R20에 대해 다음 식을 발견할 수 있다.
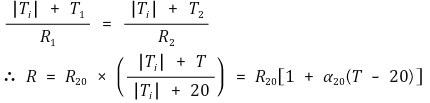
I-V 곡선의 기울기는 R이므로 다음과 같다.
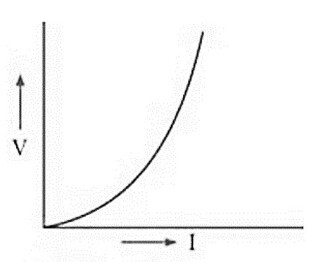
Figure. 2. 비옴물질의 I-V 곡선
3. 실험장치 및 방법 [목차]
첫째, 전원장치의 전압을 3 V로 했을 때 저항 R1에 흐르는 전류에 대하여, 전원장치의 값과 전류계의 값을 비교한다.
둘째, 전원장치의 전압을 달리 하였을 때 저항 R 1에 흐르는 전류의 크기를 측정한다.
셋째, 전원장치의 전압을 3 V로 고정하고 다음과 같은 조합의 회로에서 전체 전류를 측정한다 : R1 단독, R2 단독, R8 단독, R9 단독, R1-R2 직렬, R8-R9 병렬, R2-R8-R9 직병렬.
넷째, 각 전류값을 분석하여 옴의 법칙을 확인하고 보정한다.
4. 실험결과 [목차]
4.1. 전원장치와 전류계의 비교
정전압 전원장치는 일정한 전압을 제공하기 위한 장치이다. 본 실험에서 사용한 전원장치는 전류를 표시하는 기능이 있었는데, 전원장치의 필수적인 기능이 아니었으므로 합리적인 값을 표시해 주는지 확인해 볼 필요가 있었다. 따라서 다음과 같이 비교해 보았다.

Figure. 3. 회로도

Figure. 4. 전원장치 표시값

Figure. 5. 전류계 표시값
4.2. 전압에 따른 전류값의 추이
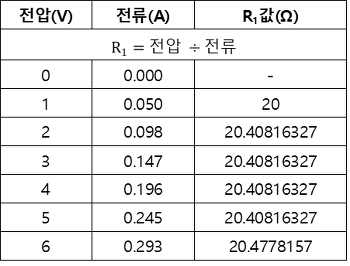
Table. 1. 전압에 따라 측정된 R1의 저항값
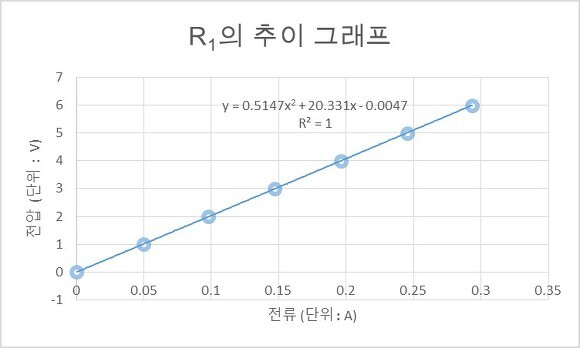
Figure. 6. R1의 추이 그래프
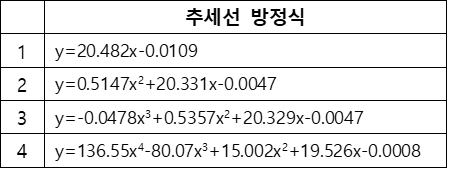
Table. 2. 다항식 차수별 추세선의 방정식
4.3. 다양한 회로에서의 전체 전류 측정
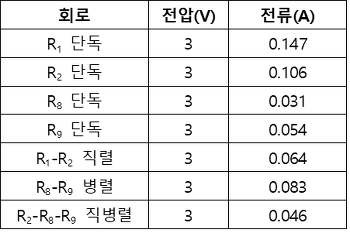
Table. 3. 다양한 회로에서의 측정값
5. 실험결론 및 논의 [목차]
5.1. 전원장치와 전류계의 차이 원인
전원장치의 표시값은 0.144 A였고, 전류계의 표시값은 0.12 A였다. 대략적으로 값이 일치한다는 점을 통해 전원장치의 표시값이 합리적인 값을 나타낸다는 것을 알 수 있다. 하지만 분명한 차이가 있다는 것도 알 수 있다.
전류계는 d’Arsonval Meter의 일종이고, d’Arsonval Meter는 다음 방정식을 따른다.
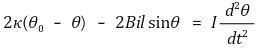
Pointer는 일시적으로 단진동을 하지만 마찰에 의해 진폭이 서서히 감소하여 우변이 0으로 수렴한다.
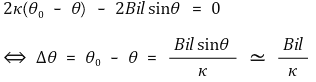
따라서 전류계에서 측정된 각변위 감소는 장치의 노후화로 인해, κ가 증가했거나 영구자석의 자기장이 감소했기 때문으로 추정해 볼 수 있다. 두 원인 모두 시간과 관계된 것으로, 구체적으로 κ의 증가는 용수철 탄성의 감소 또는 피로응력과 관련이 있고, 자기장 감소는 영구자석의 자기에너지 손실과 관련이 있다.
5.2. 내부저항 계산
전원장치는 하나의 직류회로로 간주할 수 있다. 직류회로이론에 따르면 모든 직류회로는 The’venin 등가회로로 나타낼 수 있다. 즉, 전원장치의 정확한 회로 구성은 모르더라도 하나의 독립전압원과 하나의 Rth가 직렬로 연결된 회로로 간주할 수 있다는 의미이다.
이 경우 두 가지 방법으로 내부저항 r을 계산할 수 있다. 첫 번째 방법은 R1 단독, R2 단독, R1-R2 직렬의 데이터를 이용하는 것이다. 이 경우 1.83505 Ω이 나온다. 두 번째 방법은 R2 단독, R8-R9 병렬, R2-R8-R9 직병렬의 데이터를 이용하는 것이다. 이 경우 -0.77093 Ω이 나온다. 두 방법으로 도출한 값이 다르고, 두 번째 방법에서 음의 저항값이 나왔으므로 잘못된 계산이라고 할 수 있다. 이를 보정하기 위해서 Table. 1.에서 관찰되었던, 전류에 따른 저항값의 변화를 이용해야 한다.
Figure. 1.에 따르면 다음 식이 도출된다.
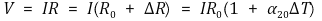
전류-전압 곡선의 적절한 추세선은 첫째 원점을 지나야 하고, 둘째 음의 계수가 없어야 한다. 전류가 0일 때 전압이 0인 것은 당연하고 실제로 관찰한 바도 있으며, 임의의 계수는 양의 물리량의 조합일 것이기 때문이다. 그 결과 Table. 2.에서 적절한 것은 2차 추세선이다.
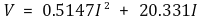
자세한 인과관계는 밝히기 어렵지만 ΔT는 전류 I에 비례하는 것으로 보인다.
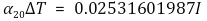
이를 통해 R1 단독, R2 단독, R8 단독, R9 단독의 결과를 보정하였다. 이를 R1-R2 직렬의 결과와 비교하여 내부저항 r을 계산하였다.
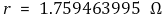
이제 R8-R9 병렬회로를 해석하려고 하는데, 병렬회로가 있는 부분에서 전체 전류와 다른 전류가 흐르므로 보정을 개별적으로 해야 한다. 하지만 마땅히 계산할 방법이 없으므로 다음 방법을 모색하였다. [1] r = 1.759463995 Ω을 이용하여 R8만의 저항과 R9만의 저항을 계산, [2] 전체 전류가 각 저항에 나뉘어 흐르는 전류값 계산, [3] R8과 R9의 증가된 저항 계산, [4] R8과 R9의 병렬 부분의 전압강하의 평균값 계산, [5] 내부저항의 전압강하를 계산, [6] 마지막으로 I0 (1 + 0.02531601987 I0)으로 나눗셈. 단, [2] 과정에서 다음 수식을 이용한다.

이때 내부저항 r은 다음과 같이 나타났다.
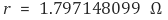
앞서 구한 값과 비교해서 상당히 유사한 값이 나왔다. 또한 전류계의 저항값은 대략 1 Ω 정도라는 상식과도 부합한다. 따라서 이와 같은 접근이 꽤 타당하다는 사실을 알 수 있다.
하지만 한계 또한 존재한다. 우선 위 계산에서 α20ΔT가 일정하다는 가정이 있었는데, 이는 각 저항이 동일한 재질로 이루어져 있음을 함축한다. 이를 직접 확인해야 하는 대목이다. 또한 [1] ~ [6]에 해당하는 과정 중 [2] 과정에서 불필요한 근사 과정이 있었다. 그 결과 실제로 병렬연결이면서 R8과 R9의 전압강하가 달라 [4]와 같은 과정이 필요했다. 근사 없이 계산할 수 있는 방법을 연구해야 할 것이다. 또한 ΔT와 전류 I가 정말 1차 비례하는지 검증하고 규명해야 한다. 열전달 이론에 따르면 ΔT는 I2에 비례한다고 예측하기 때문이다.
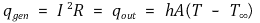
입력: 2019.06.29 00:53
'▶ 자연과학 > ▷ 일반물리학' 카테고리의 다른 글
| 【물리학】 물리학 실험 목차 (0) | 2019.07.11 |
|---|---|
| 【물리학 실험】 7강. 등전위선 실험 (7) | 2019.06.29 |
| 【물리학 실험】 5강. 공명 실험 (0) | 2019.06.29 |
| 【물리학 실험】 4강. 단진동 실험 (0) | 2019.06.28 |
| 【물리학 실험】 3강. 관성모멘트 실험 (0) | 2019.06.28 |




최근댓글