광학 3강. 양자광학 1부
추천글 : 【물리학】 물리학 목차
1. 빛의 역사 [본문]
2. 빛의 본질 [본문]
3. 다른 광학과의 비교 [본문]
a. 양자광학 2부
1. 빛의 역사 [목차]
⑴ 개요
① 파동설(wave theory) : 빛은 파동이라는 학설
② 입자설(corpuscular theory) : 빛은 입자라는 학설
③ 빛 연구의 역사는 빛이 파동인지 입자인지를 규명하는 역사라고 할 수 있음
⑵ 근대까지의 역사
① 아리스토텔레스(Aristole) (BC. 384-322) : 우리가 세상을 볼 때 우리 눈에서 나온 무언가가 물체에서 반사되어 보는 것
② 이븐 알하이삼(Hasan Ibn al Haytham) (965-1040) : 눈의 해부 구조와 바늘구멍 사진기의 유사성을 주장
③ Francesco Maria Grimaldi (Bologna) : 1660년 빛의 회절을 입자설로 설명
④ 호이겐스(Huygens) : 빛의 파동설 주장. 반사와 굴절을 효과적으로 설명
○ Treatise on light (1690)
○ 빛은 에테르(aether)라는 매질 상을 이동하는 파동이라고 생각
⑤ 뉴턴 : 빛은 Corpuscle이라는 입자라고 주장
○ Opticks (1704)
⑥ 회절실험
⑦ 산란실험
⑧ 토마스 영(Thomas Young) (1773-1829)
○ 이중슬릿 간섭 실험(1801-1803)
○ 빛의 파장 측정
⑨ 프레넬(Augustine Fresnel) (1788-1827)
○ 빛의 파동성 주장
○ 호이겐스의 원리로부터 회절현상에 관한 방법론 개발(1818)
⑩ 맥스웰(James Clerk Maxwell) (1831-1879)
○ 전기와 자기에 관한 수학적인 이론을 4개의 맥스웰 방정식으로 정립
○ 전자기파의 전파에 관한 이론을 발표(1873)
○ 전자기파의 속도를 계산한 결과 기존에 알려진 빛의 속도와 동등함을 발견
⑪ 헤르츠(Heinrich Hertz) (1857-1894) : 맥스웰이 예측한 전자기파를 만들고 검출(1887)
⑶ 광전효과(photoelectric effect) : 아인슈타인의 해석으로 빛의 입자성 증거로 채택
① 개요
○ 정의 : 입사된 빛이 금속판과 충돌하여 광전자가 튀어 나오는 현상
○ 일함수 : 광전효과가 일어나기 위한 최소한의 에너지, 곧 이온화에너지
○ 한계진동수 : 광전효과가 일어나기 위한 빛의 최소한의 진동수. h × 한계진동수 = 일함수
○ 광자의 최대 운동에너지 : 입사광의 에너지 - 일함수
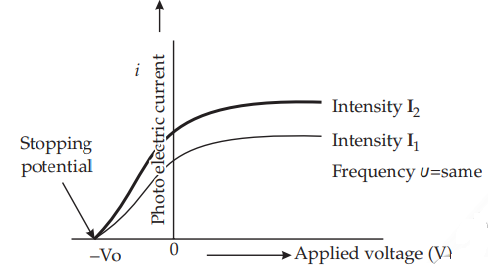
Figure. 1. 전압과 광전효과 전류, 빛의 세기의 관계
② 물질과 빛의 상호작용 관련

Figure. 2. 에너지 준위과 광전효과
○ X = a, Y = b, Z = c
○ X, Z를 따로 비추어도 광전자가 방출되지 않음. Y를 비추면 광전자가 방출됨
○ 광자 Y의 에너지는 광자 X의 에너지와 광자 Z의 에너지의 합과 같음
○ X와 Z를 동시에 비추어도 P에서 광전자가 방출되지 않음
○ 이유 : 하나의 원자와 상호작용하는 광자는 기껏해야 1개인 듯
③ 응용
○ 광 다이오드
○ 전하 결합 소자(CCD)
○ X선 광전자 분광법(XPS, X-ray photoelectron spectroscopy)
⑷ 흑체복사(black body radiation)
① 정의 : 에너지를 가진 모든 물체가 빛을 발하는 현상
② 흑체(blackbody) : 입사된 에너지를 모두 흡수하고, 흡수한 모든 에너지를 완전히 방출하는 물체
③ 파동의 상태수 개수(number of modes)
○ 현에서의 정상파를 기준으로 함
○ 1차원 정상파 : 현의 길이가 L일 때, 파동의 상태수 n (단, n은 자연수)에 따라 다양한 진동수의 정상파가 존재함
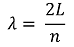
○ 3차원 정상파 : 파동의 상태수 벡터 (l, m, n)에 따라 다양한 진동수의 파동(이 경우, 빛)이 존재함
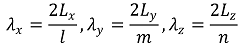
○ 상태수 벡터를 직교좌표계에 대응시킬 수 있음 : l, m, n이 양의 정수이기 때문에 1/8구(octant)를 고려함
○ 파동의 상태수 개수 : 원점으로부터의 거리를 p, 반지름이 p인 1/8 구 내 격자점의 개수를 N*(p)라 할 때,
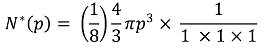
○ 상태수 개수(N*)와 진동수(ν)의 관계
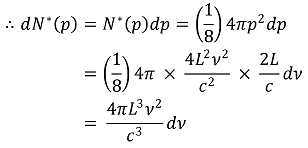
○ 위 식은 같은 상태수여도 위상이 반대인 2개의 파동이 있을 수 있다는 것을 고려하지 않음
○ 결론 : 공간의 부피 V = L3, 단위 부피당 상태수 개수 N = N* / V에 대하여,
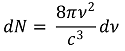
④ 레일리-진스 법칙(Rayleigh-Jeans law)
○ 개요 : 흑체복사를 파동성으로 분석하려고 하면 UV 파탄이 관찰돼야 함
○ 열역학에서 계의 평균 진동 에너지 : 각 방향에 대한 병진, 회전과 달리 진동 그 자체로 자유도 2를 할당함
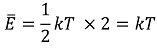
○ 진동수 ν에서 단위 부피당 평균 방사 에너지
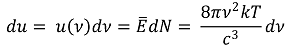
○ UV 파탄(UV catastrophy) : 흑체가 파장이 0 근처의 빛을 무한대 가깝게 발산하는 것
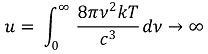
○ 실제로는 파장이 0 근처의 빛은 세기가 0으로 수렴
⑤ 플랑크 법칙(Planck's law)
○ 막스 플랑크(Max Planck)가 입자성을 도입하고 E = hν를 가정하여 성공적으로 설명 (1900년)
○ 광자 한 개의 에너지
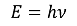
○ 진동수가 ν인 광자가 n개 있을 확률 : 특정 에너지의 입자의 확률이 지수함수라는 맥스웰-볼츠만 분포에서 착안

○ 계의 평균 에너지
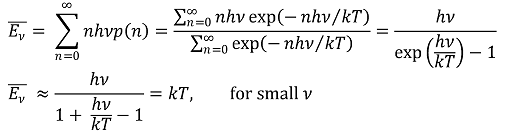
○ 진동수 ν에서 단위 부피당 평균 방사 에너지
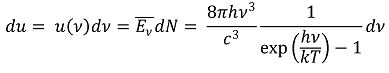
○ 플랑크 곡선 : 흑체에서 방출하는 복사에너지의 파장에 따른 분포. 흑체의 복사에너지 분포는 온도에만 관계함
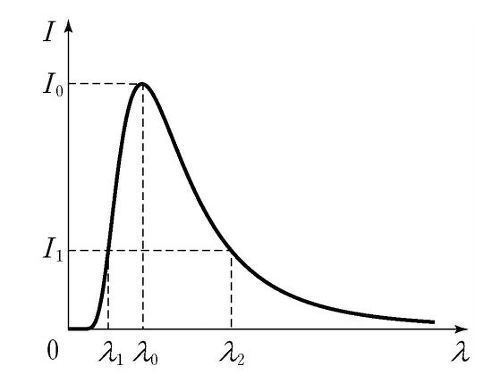
Figure. 3. 플랑크 곡선
○ 계의 단위 부피당 전체 에너지
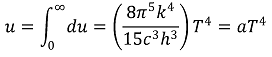
○ 광자의 플럭스

⑥ 스테판-볼츠만 법칙(Stefan-Boltzmann law) : 흑체가 단위면적당 단위시간에 방출되는 에너지는 흑체의 절대온도 T(K)의 네제곱에 비례
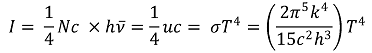
○ 실제 물체의 경우 위 식에서 반사율 ε을 곱해주기도 함
○ 단, σ : 볼츠만 상수, 8.22 × 10-11
⑦ 빈의 변위 법칙(Wien's displacement law) : 최대 복사 에너지를 내는 파장 λmax (㎛)은 흑체의 절대온도 T(K)에 반비례
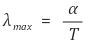
○ 단, α : 빈의 상수, 2.89 × 103
⑧ 파울리 배타원리
○ 정의 : 한 궤도 상에 모든 양자수가 동일한 전자가 둘 이상 존재할 수 없음
○ 플랑크 곡선이 연속적인 그래프로 나오는 이유
○ 많은 원자들이 모여 있으면 에너지 준위들이 겹치다가 약간씩 밀려나면서 에너지 준위가 연속적으로 나타남
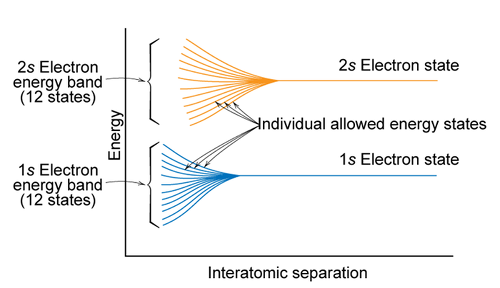
Figure. 4. 오비탈 중첩에 따른 에너지 준위의 갈라짐
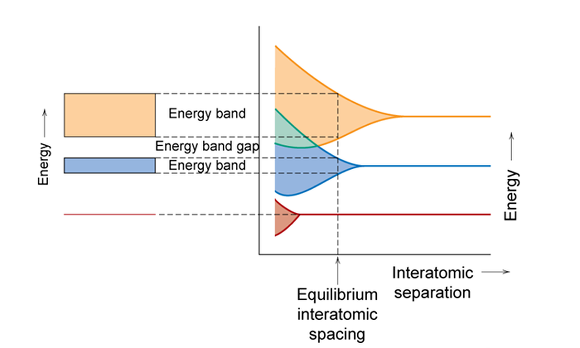
Figure. 5. 오비탈 중첩에 따른 에너지 밴드의 형성
⑸ 콤프턴 산란(Compton scattering)
① 정지한 전자에 빛을 입사시키면 광자와 전자가 탄성충돌을 하는 현상
② 빛의 입자성 증거
③ 실험설계
⑹ 전자의 파동성
① 데이비슨·거머 실험 : 전자선을 니켈 결정에 입사시킬 때 회절 현상이 나타남을 보임
② 톰슨의 전자 산란 실험(1925년)
○ 전자선을 금속박에 입사시켜 X선의 회절과 닮은 전자의 회절 사진을 얻음

Figure. 6. 톰슨의 전자 산란 실험
왼쪽은 X선 회절 무늬이고 오른쪽은 전자선 회절 무늬임
○ 결론 : 당연히 입자라고 알려진 전자가 회절이 가능하다는 것을 실험으로 입증
○ 추론 : 전자가 파동의 성질을 가지면 정확한 궤도를 알 수 없음
2. 빛의 본질 [목차]
⑴ 빛은 전자기력을 전달하는 전자기파
⑵ 광속불변의 법칙
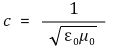
⑶ 정지질량 = 0
m0 = 0
⑷ 스핀이 1인 벡터입자
⑸ 전하가 0
3. 다른 광학과의 비교 [목차]
⑴ 기하광학 ⊂ 파동광학 ⊂ 양자광학
⑵ 기하광학 : 빛을 광선으로 간주
⑶ 파동광학 : 빛을 파동으로 간주
⑷ 양자광학 : 빛을 입자로 간주. 파인만 diagram이 사용. 500 nm 광자 1개의 에너지 E = hf = hc / λ = 3.98 × 10-19 J
입력: 2020.03.23 23:03
수정: 2022.09.12 19:42
'▶ 자연과학 > ▷ 일반물리학' 카테고리의 다른 글
| 【물리학】 광학 7강. 응용광학 (0) | 2020.05.24 |
|---|---|
| 【물리학】 광학 4강. 양자광학 2부 (0) | 2020.05.24 |
| 【물리학】 물리학 목차 (0) | 2020.01.12 |
| 【물리학】 현대물리학 2강. 상대성이론 (0) | 2019.07.28 |
| 【물리학】 물리학 실험 목차 (0) | 2019.07.11 |




최근댓글