9강. 기체
추천글 : 【화학】 화학 목차
1. 개요 [목차]
⑴ 종류 : 표준상태(25 ℃, 1 atm)에서 기체로 존재하는 원소에 대해
① 단원자 기체 : He, Ne, Ar, Kr, Xe, Rn (비활성기체, 8A족 원소)
② 이원자 기체 : H2, N2, O2, F2, Cl2 등
⑵ 물리적 특성 : 대부분의 기체들은 상당히 유사한 물리적 성질이 있음
① 담겨있는 용기의 부피와 모양으로 나타냄
② 가장 잘 압축될 수 있는 물질의 상태
③ 액체, 고체보다 밀도가 훨씬 작음
④ 기체의 종류와 관계없이 일정한 법칙을 보임
⑶ 표준상태
① STP(standard temperature and pressure) : 0 ℃, 1 atm
○ 기체 1 mol의 부피 = 22.4 L
② SATP(standard ambient temperature and pressure) : 25 ℃ , 1 bar
③ NTP(normal temperature and pressure) : 20 ℃, 1 atm
○ 기체 1 mol의 부피 = 22.4 × 293.15 ÷ 273.15 = 24.04 L
④ ATP(actual temperature and pressure) : 실제 온도와 실제 기압
2. 기체 연구의 역사 [목차]
⑴ 토리첼리 실험
① 실험 과정 : 수은주 모세관을 뒤집어 놓으면 항상 높이가 일정함
② 응용 : 대기압 측정 실험

⑵ 보일의 법칙(Boyle's law)
① 1662년 R. Boyle이 발표
② 일정한 온도에서 일정한 양의 기체의 부피는 그 압력에 비례 (P ≪ 1)
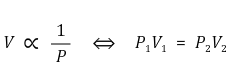
⑶ 샤를-게이뤼삭의 법칙(Charles' law)
① 1787년 J.A.C. Charles가 발표
② 압력이 일정할 때 기체의 부피는 온도에 비례

③ 절대온도(absolute temperature, Kelvin temperature)의 도입
○ 절대영도는 V - T 곡선에서 직선형의 그래프를 연장하여 x축과 만나는 지점
○ 실제로는 온도가 떨어지면 기체가 액화나 승화를 하므로 외삽점을 확인할 수 없음
○ 하지만 모든 기체는 동일한 외삽점을 가지므로 특별한 의미가 있다고 보고, 절대영도 및 절대온도 개념 도입
⑷ 아보가드로 법칙(Avogadro's law) : 온도, 압력이 일정할 때 + (P ≪ 1)
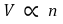
① 표준 기압(1 bar)과 표준 온도(0 ℃)에서 기체 1 mol의 부피는 22.4 L
⑸ 이상기체상태방정식(ideal gas equation) : 기체의 종류에 관계없이
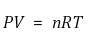
① 기체상수(gas coefficient) : R로 표시
○ 8.31446 J / mol·K
○ 8.20574 × 10-2 L·atm / K·mol
○ 287 J / kg·K : 팁. 공업 열역학에서 자주 사용
② 특정 조건(압력 ≪ 1)에만 성립하는 제한 법칙(limiting law)
⑹ 달톤(Dalton)의 부분압력의 법칙 : 부분압력 비율은 기체의 개수 비율과 같음
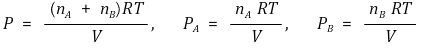
3. 기체분자운동론 : 이상기체(ideal gas)의 모델을 서술 [목차]
⑴ 기체분자운동론 규칙
① 규칙 1. 기체는 연속적으로 랜덤워크(random walk) 운동을 함
② 규칙 2. point mass : 기체분자의 부피는 무한히 작음(infinitesimal volume)
③ 규칙 3. 기체 입자는 직진 운동만 함
④ 규칙 4. no interaction : 기체는 충돌 이외에 어떤 상호작용도 하지 않음
⑤ 규칙 5. elastic collision : 기체의 충돌은 완전 탄성충돌
⑥ 규칙 6. 에너지 등분배의 법칙(energy equipartition law) : 기체 분자의 평균 운동 에너지는 온도에 비례
○ 수식화
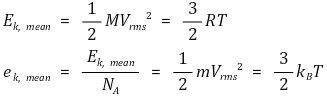
○ (참고) 열역학 제0법칙 : 두 온도가 같다는 것을 열평형으로서 정의
○ (참고) 온도 눈금의 실험적 정의 : 온도계의 열팽창
○ 수은 온도계 : 은색 온도계
○ 알콜 온도계 : 빨강 온도계. 염료에 의해 빨갛게 보임
○ 물리적 의미 : 기체 분자의 운동 에너지가 온도에 선형 비례하도록 온도 눈금을 정의
○ 열역학에서 내부에너지가 온도에 대한 함수인 것을 직접적으로 유도
⑵ 이상기체상태방정식의 물리화학적 유도
① 1st. x축과 수직한 우측면의 압력을 구한다고 생각하자.
② 2nd. 기체 분자가 끊임없이 탱탱볼처럼 벽과 탄성충돌을 한다는 것을 염두하자.
③ 3rd. 주기 : 기체 분자 한 개가 우측면에 충돌하는 주기
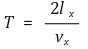
④ 4th. 기체 분자 한 개가 우측면으로 향하며 운동하다가 충돌 후 우측면에서 멀어지며 운동함을 상기
⑤ 5th. 힘 : 기체 분자 한 개가 우측면에 평균적으로 작용하는 힘 : 힘 = Fa = 운동량의 변화율 = dp / dt
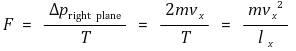
⑥ 6th. 비약적 가정 : 과학은 가끔 위험한 가정을 할 때가 있는데 결과가 아름다우므로 용서됨
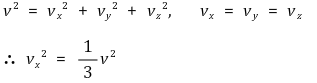
⑦ 7th. 압력 도출 : 압력의 정의 P = F / A를 이용
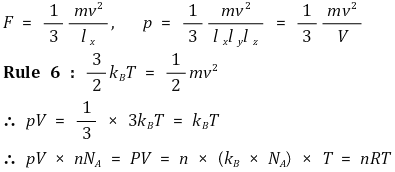
⑧ 8th. 단위 시간당 벽면에 부딪히는 충돌하는 분자의 평균 개수
○ 단위 시간당 한 개의 면에 부딪히는 충돌하는 분자의 평균 개수
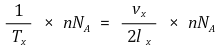
○ 단위 시간당 전체 벽면에 부딪히는 충돌하는 분자의 평균 개수

4. 기체의 물리화학적 분석 [목차]
⑴ 그레이엄의 법칙(Graham's law)
① 확산(diffusion) : 분자간 충돌을 동반하여 특정 물질이 다른 물질에 섞여 들어가는 것
② 분출(effusion) : 특정 입자가 높은 압력에서 낮은 압력으로 이동하는 경우 (예 : 진공 내 입자의 이동)
③ 그레이엄의 법칙
○ 내용 : 분출속도 ∝ 1 / √M
○ 유도 : 같은 온도이기 때문에 운동에너지가 같을 것
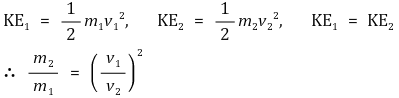
○ 확산속도에도 그레이엄의 법칙을 적용할 수 있음
○ 맨허튼 프로젝트에서 우라늄 농축 시에 응용
④ 기체가 벽면에 충돌하는 빈도
○ 분출속도에 비례
○ 기체가 벽면에 충돌하는 빈도 ∝ 몰수 / 부피 × 평균속력
⑵ 기체분자운동론의 함의 : 제곱평균제곱근(root mean square) 속력 vrms
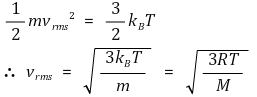
⑶ 맥스웰-볼츠만 속도 분포(Maxwell-Boltzmann speed distribution)
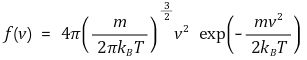
① m : 분자 한 개의 질량. T : 절대온도. kB : 볼츠만 상수
② 의미 1. 전체의 합이 1이 되도록 하기 위한 설정

③ 의미 2. 정규분포함수의 형태
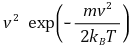
④ 의미 3. 제곱평균제곱근 속력 식을 맞추기 위한 설정
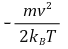
⑤ 결과 1. 제곱평균제곱근 속도(vrms, root mean square velocity)

⑥ 결과 2. 평균속도(vavg, average velocity) : 적분을 통해 구할 수 있음
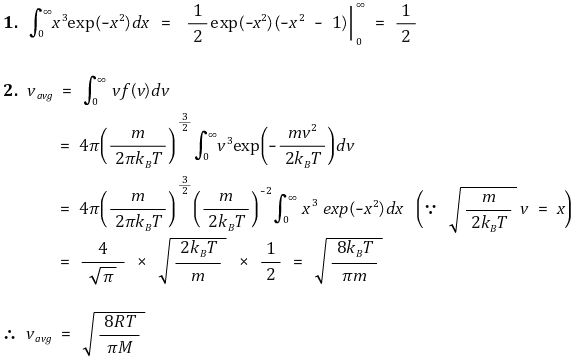
⑦ 결과 3. 최빈속도(vmp, most probable velocity) : 미분을 통해 극값을 구하면 최빈속도를 구할 수 있음
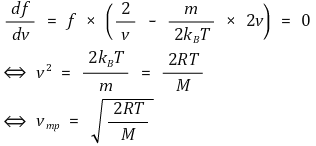
⑧ 결과 4. 상대속도(vrel, relative velocity)
⑨ 분자량이 무거울수록, 온도가 낮을수록 속도 분포가 잘 맞음 : (주석) 가벼운 분자는 빠른 속도에서 톡톡 튀므로
5. 실제 기체 [목차]
⑴ 압축성 인자(Z, compressibility factor) : 이상기체와 실제기체의 부피 비
① 정의
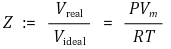
② 분자간 상호작용 판단
○ Z < 1 : 인력(attraction force)이 우세. 온도가 높고 압력이 낮은 조건
○ Z > 1 : 척력(repulsive force)이 우세. 온도가 낮고 압력이 높은 조건
○ 팁. 온도가 높으면 이상기체와 가까워지므로 Z = 1에 가까워짐
③ 수소 : 매우 약한 분자간 힘을 가짐
⑵ 반데르발스 방정식(van der Waals equation of state) : 실제 기체의 상태방정식에 대한 한 가지 모형
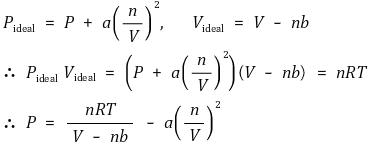
① 상수 a : 기체 분자의 인력에 의한 압력 감소를 보정하기 위한 상수
○ 'attraction'의 a
○ 상호작용은 2개 분자의 관계이므로 분자 간 인력은 nC2 = n(n-1) / 2와 관련하여 (n / V)2에 비례하게 됨
○ a > 0 : attractive, 극성이 큼
○ a < 0 : repulsive, 극성이 작음
② 상수 b : 기체 분자 자체가 차지하는 부피를 보정하기 위한 상수
○ b는 기체 분자 크기의 약 2배 정도임
③ 압축인자와의 관계
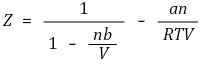
④ (참고) 기체-액체 평형상태에서 임계점을 제외하고 3개의 부피해를 가짐
⑤ (주석) 어거지로 맞춘 식인데 의외로 잘 맞아서 유명해진 식으로 보임
⑶ 비리얼 상태방정식(Virial equation)
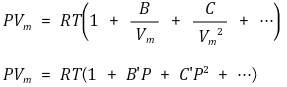
① B, C, B', C', ··· : Virial coefficient (온도에 대한 함수)
입력: 2018.12.27 20:34
'▶ 자연과학 > ▷ 일반화학' 카테고리의 다른 글
| 【화학】 10강. 액체와 고체 (4) | 2018.12.27 |
|---|---|
| 【화학】 12강. 혼합물의 분리 (0) | 2018.12.27 |
| 【화학】 8강. 물질의 상태 (0) | 2018.12.27 |
| 【화학】 7강. 양자역학 4부 - 밴드갭 이론 (0) | 2018.12.27 |
| 【화학】 6강. 양자역학 3부 - 오비탈 이론 (15) | 2018.12.27 |





최근댓글