4강. 밀폐계의 에너지 해석
추천글 : 【열역학】 열역학 목차
1. 이동경계일 [본문]
2. 밀폐계에 대한 에너지 평형 [본문]
3. 비열 [본문]
4. 이상기체의 내부에너지, 엔탈피 및 비열 [본문]
5. 실제 기체의 내부에너지, 엔탈피 및 비열 [본문]
6. 고체와 액체의 내부에너지, 엔탈피 및 비열 [본문]
1. 이동경계일(moving boundary work) [목차]
⑴ 피스톤과 같은 계의 팽창 또는 압축 동안 경계를 통해 수행되는 일 (열이 아님)
⑵ 일은 경로함수가 아님
① 따라서 실제 기관이나 압축기에서 경계일은 직접적인 측정에 의해 구함
⑶ 준평형과정(≒ 준정적 과정)에서 열기관은 최대의 출력일을 내고, 압축기는 최소의 입력일을 취함
⑷ 피스톤이 준평형 과정으로 거리 ds만큼 움직인다면, 이 과정 동안 수행된 미소일은

① 결과가 음수이면 입력 경계일 또는 압축일을 나타냄
⑸ 만약 일이 경로함수가 아니면 자동차 기관이나 원동소와 같이 사이클로 동작하는 장치가 열을 발생시킬 수 없음
⑹ 수식화

⑺ 폴리트로픽 과정(polytropic process)
① PVn = C = const 또는 P = CV-n = f(V)
○ n = 0 : 정압과정
○ n = 1 : 등온과정
○ n = γ = CP / CV : 가역단열과정
○ n = ∞ : 정적과정
② 일에 대한 수식화
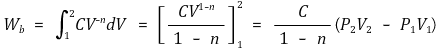
○ 이상기체에서는 PV = mRT이므로
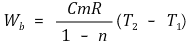
○ n = 1인 경우는 특별함
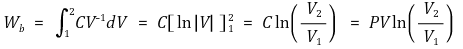
③ 열에 대한 수식화 : 팁. 암기할 것
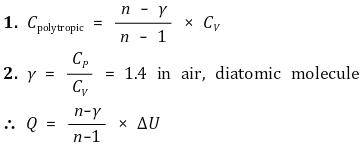
○ Cn := (n-γ) / (n-1)를 폴리트로프 비열이라고 함
2. 밀폐계에 대한 에너지 평형 [목차]
⑴ 기본식
① 일반식
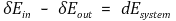
② 사이클 과정

⑵ Q = E + W ⇒ Wnet, in = Qnet, in 또는 Wnet, out = Qnet, out (사이클 과정에서)
⑶ 부호 규약
① 계로 전달된 열(입력열)은 양의 Q의 값으로 취함
② 계에 의해 수행된 일(출력일)은 양의 W 값으로 취함
⑷ 열과 일은 동일한 에너지지만 열역학 제2법칙의 관점에서 보면 열과 일은 매우 다름
① 열은 low-quality energy
② 일은 high-quality energy
3. 비열(specific heat) [목차]
⑴ 정의 : 단위 질량의 물질을 단위 온도 올리는데 필요한 에너지. 어떻게 실행되느냐에 따라 다름
① 어떤 물질을 단위 온도만큼 올리는 데 필요한 에너지는 온도와 압력에 따라 다르나 그 차이는 크지 않음
② 비열보다는 비에너지가 더 적합한 표현임
⑵ 정적 비열(specific heat at constant volume) CV : 체적이 일정한 조건의 비열
① 수식화
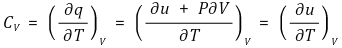
② 상태량의 조합으로 구성되므로 정적 비열도 상태량임
③ 물질의 내부에너지는 에너지 전달의 형태에 따라서도 변화할 수 있음
⑶ 정압 비열(specific heat at constant pressure) CP : 압력이 일정한 조건의 비열
① 수식화

② 상태량의 조합으로 구성되므로 정압 비열도 상태량임
③ 물질의 엔탈피는 에너지 전달의 형태에 따라서도 변화할 수 있음
4. 이상기체의 내부에너지, 엔탈피 및 비열 [목차]
⑴ 이상기체의 내부에너지는 온도만의 함수 : 줄(Joule)에 의해 1843년 증명됨
① 단순한 이해
○ (참고) 열역학 제0법칙 : 두 온도가 같다는 것을 열평형으로서 정의
○ (참고) 온도 눈금의 실험적 정의 : 온도계의 열팽창
○ 수은 온도계 : 은색 온도계
○ 알콜 온도계 : 빨강 온도계. 염료에 의해 빨갛게 보임
○ 기체 분자 운동론의 에너지 등분배의 법칙
○ 자유도가 γ인 기체 분자 1개의 에너지
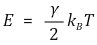
○ 물리적 의미 : 기체 분자의 운동 에너지가 온도에 선형 비례하도록 온도 눈금을 정의
○ 기체 분자 운동론은 계의 내부 에너지가 운동 에너지로만 표현되는 것으로 가정
○ 일반적인 기체 : 퍼텐셜 에너지가 관여
○ 1st. 기체 분자 운동론의 운동 에너지가 온도에 선형 비례
○ 2nd. 일반적인 기체의 역학적 에너지도 온도에 선형 비례
○ 3rd. 그 기체의 역학적 에너지가 바로 내부에너지
○ 고체 및 액체
○ 1st. 부피 팽창이 거의 없음
○ 2nd. 계의 일이 거의 없음
○ 3rd. 내부에너지 등의 상태량과 압력은 연관성이 없음
○ 4th. 내부에너지는 오직 온도에 대한 함수
② 엄밀한 이해 : 내부에너지가 온도에 대한 함수임을 증명
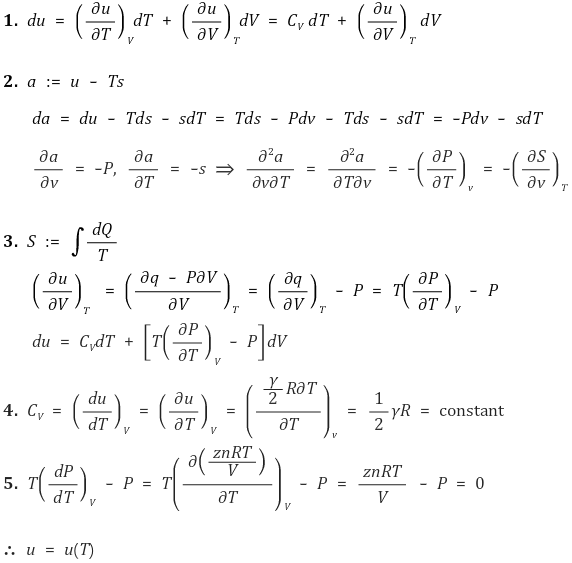
○ 일반적인 기체라 하여도 이상기체 상태방정식 PV = nRT와 유사한 PV = znRT가 성립한다고 가정할 수 있음
○ 네 번째 식인 에너지 등분배의 법칙이 핵심임
⑵ 이상기체의 엔탈피도 온도만의 함수
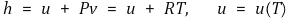
⑶ 이상기체의 내부에너지와 엔탈피의 미소변화

⑷ 이상기체의 내부에너지와 엔탈피 변화를 계산하는 방법
① 수표화된 u와 h 값을 이용 : 이 방법은 표가 있을 때 가장 쉽고 가장 정확한 방법
② 온도의 함수로써 표현된 CV, CP의 관계식을 이용 : 컴퓨터로 계산하는 게 바람직
③ 평균비열을 이용 : 온도 구간이 아주 크지 않다면 상당히 정확
⑸ 이상기체의 비열 관계식
① CP = CV + R
② 비열비(specific heat ratio) k = CP / CV
○ 단원자 기체 : CP / CV = (5/2) / (3/2) = 1.6667
○ 공기를 포함한 대부분의 이원자 기체 : CP / CV = (7/2) / (5/2) = 1.4
○ 3개 이상의 원자를 포함하는 기체 : CP / CV = (9/2) / (7/2) = 1.2857
○ 단원자 기체가 아닌 경우 CV가 예상보다 크기 때문에 (즉, 용량이 더 크기 때문에) 비열비가 더 작게 측정됨
5. 실제 기체의 내부에너지, 엔탈피 및 비열 [목차]
⑴ 줄-톰슨 계수(Joule-Thomson coefficient) : 조름공정(throttling process)에서 실제 기체의 거동
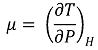
6. 고체와 액체의 내부에너지, 엔탈피 및 비열 [목차]
⑴ CP는 CV보다 항상 큼 : 팽창일을 포함하기 때문
① 고체 및 액체 등의 비압축성 물질은 팽창일을 포함하지 못하기 때문에 다음 관계식을 가짐
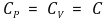
⑵ 내부에너지 변화 : 부피가 거의 변하지 않아 관련 요인이 아님
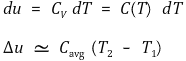
⑶ 엔탈피 변화
① 기본 수식
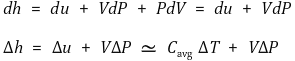
② 가열기의 정압과정 (ΔP = 0) : Δh = Δu ≃ Cavg ΔT
③ 펌프의 등온과정(ΔT = 0) : Δh = rΔP
입력: 2019.04.22 19:07
'▶ 자연과학 > ▷ 열역학' 카테고리의 다른 글
| 【열역학】 6강. 열역학 제2법칙 (0) | 2019.04.18 |
|---|---|
| 【열역학】 5강. 검사체적의 질량 및 에너지 해석 (0) | 2019.04.18 |
| 【열역학】 3강. 순수물질의 상태량 (0) | 2019.04.18 |
| 【열역학】 2강. 에너지, 에너지 전달 및 에너지 분석 (0) | 2019.04.18 |
| 【열역학】 1강. 기본 개념 (0) | 2019.04.18 |




최근댓글