7강. 양자역학 4부 - 밴드갭 이론(band-gap theory)
추천글 : 【화학】 화학 목차
1. 밴드갭 이론 [본문]
2. Bloch 정리 [본문]
3. Kronig-Penny model [본문]
4. 에너지 밴드와 브릴루앙 영역 [본문]
5. E-k diagram [본문]
6. k의 의미 [본문]
7. 유효질량 개념 도입 [본문]
8. 캐리어와 전류 [본문]
9. 응용 [본문]
a. 양자역학 1부
b. 양자역학 2부
c. 양자역학 3부
d. 양자역학 4부
1. 밴드갭 이론(band-gap theory) [목차]
⑴ 개요
① 정의 : 자유입자가 아닌 구속된 원자에 대한 퍼텐셜 에너지를 분석하는 이론
② 반도체를 설명하는 이론
⑵ 페르미-디랙 통계
① 페르미-디랙 분포
○ 정의 : 임의의 온도 T에서 에너지 준위 E가 입자에 의해 채워질 확률
○ 격자 구조 내부의 원자가전자들은 페르미-디랙 분포를 따름
② 페르미 준위
○ 정의 : 0 K에서 고체 내의 전자가 가질 수 있는 가장 높은 에너지 준위
○ 이렇게 정의된 페르미 준위는 임의의 온도에서 전자가 채워질 확률이 절반이 됨
○ 페르미 준위에서 특정 에너지를 초과한 일정 비율의 전자들은 원자핵의 퍼텐셜을 무시하여 자유전자가 됨
③ 페르미 기체
○ 페르미 기체 (자유전자기체) : 상호작용이 없는 페르미온들의 집합
○ 파울리 배타원리에 의해 절대영도에서 페르미 기체의 평균 에너지는 바닥상태 단일 입자보다 큼
○ 축퇴압력 : 파울리 배타원리에 의해 절대영도에서 페르미 기체의 압력은 0이 아닌 값을 나타냄
2. Bloch 정리 [목차]
⑴ 정의 : 퍼텐셜 에너지 U(x)가 주기적이고 U(x+a) = U(x)이면 다음을 만족
⑵ 수식화
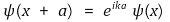
3. Kronig-Penney model [목차]
⑴ 정의
Figure. 1. Kronig-Penny model
⑵ 가정
① 결정이 무한하다고 가정
② 결정구조는 계단식 퍼텐셜을 가진다고 가정
⑶ 수식화
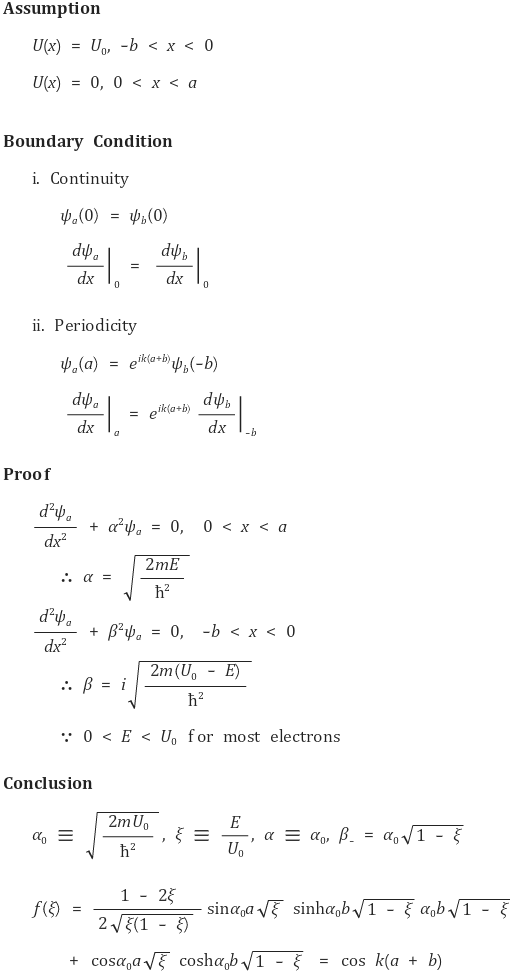
4. 에너지 밴드(energy band)와 브릴루앙 영역(Brillouin zone) [목차]
⑴ 해석 1. 수학적 해석
① 퍼텐셜 에너지 f(ξ)는 요동치는 값
② cos k(a+b)가 -1 ~ 1 사이의 값을 가짐
③ ξ이 커짐에 따라 해의 부존재 → 해의 존재 → 해의 부존재 → ···
④ 결론 : 에너지 준위는 밴드의 형태로 나타남
⑵ 해석 2. 파울리 배타원리
① 파울리 배타원리 : 한 궤도 상에 모든 양자수가 동일한 전자가 둘 이상 존재할 수 없음
② 많은 원자들이 모여 있으면 에너지 준위들이 겹치다가 약간씩 밀려나면서 에너지 준위가 밴드의 형태로 나타남
Figure. 2. 오비탈 중첩에 따른 에너지 준위의 갈라짐
Figure. 3. 오비탈 중첩에 따른 에너지 밴드의 형성
⑶ 해석 3. 쿨롱의 법칙
① 전자끼리는 척력이 발생하므로 에너지 준위가 미세하게 갈라짐
② 많은 원자들이 모여 있으면 에너지 준위들이 약간씩 밀려나면서 에너지 준위가 밴드의 형태로 나타남
⑷ 에너지 밴드의 분류
① 에너지 밴드(energy band) : 해가 존재하는 연속구간
② 금지대역 밴드갭(금지대, forbidden band) : 해가 존재하지 않은 연속구간 (단, 최초의 구간은 제외)
③ 밴드갭(에너지갭, 띠틈, band gap, energy gap) : 가전자를 자유전자로 만들기 위한 에너지
④ 에너지 밴드는 다시 가전자대(valence band)와 전도대(conduction band)로 구분
⑤ (참고) 단일 원자의 가전자대, 전도대
○ 마그네슘 원자의 가전자대는 1s, 2s, 2p, 3s 오비탈들을 지칭함
○ 마그네슘 원자의 전도대는 3p, 4s, 3d 등 3s 이후의 오비탈들을 지칭함
5. E-k diagram [목차]
⑴ k ∈ [-π / (a + b), π / (a + b)]
⑵ k = 0, ± π / (a + b)에서 E-k diagram의 기울기가 0임 : Kronig-Penney 모델뿐만 아니라 실제로도 관찰
⑶ 주기성에 의해 선택된 범위 밖의 E-k 해는 선택된 범위 안의 E-k 해와 중복됨
⑷ 하나의 허용된 에너지당 오직 두 개의 k 값이 가능 (∵ 원점에 대한 대칭성)
⑸ E-k diagram을 적당히 펼치면 포물선과 유사하고 에너지가 높을수록 수렴함
Figure. 5. E-k diagram을 적당히 펼친 것
⑹ (참고) 실제 E-k diagram은 굉장히 복잡하지만 밴드 끝 부분의 상단과 하단에서 일반적으로 포물선의 형태
⑺ (참고) 자유입자도 E-k diagram이 포물선 모양 (∵ E ∝ p2, p ∝ k)
6. k의 의미 [목차]
⑴ 자유입자에서 k = 파수, hk = p
⑵ 주기적인 전위에서 k = 파수, hk = 결정운동량
⑶ 결정 안에 있는 전자의 실제 운동량이 아니라 결정 내 상호작용 및 운동량과 관련된 상수
7. 유효질량 개념 도입 [목차]
⑴ 유효질량
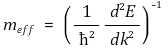
⑵ E-k diagram에서 모든 밴드의 하단 근처에서 아래로 볼록 : meff > 0 (전자)
⑶ E-k diagram에서 모든 밴드의 상단 근처에서 위로 볼록 : meff < 0 (정공)
⑷ 밴드의 끝 부분은 일반적으로 포물선 → 두 번 미분하면 상수 → 유효질량이 상수
8. 캐리어와 전류 [목차]
⑴ 각 밴드의 원자가 N개, 원자당 전자가 2개, 상온인 경우
Figure. 7. 각 밴드의 원자가 N개, 원자당 전자가 2개, 상온인 경우
⑵ Band 4 : 전부 empty
⑶ Band 3 : 대부분 empty
⑷ Band 2 : 대부분 full
⑸ Band 1 : 전부 full
⑹ Band 4는 전자가 없어 알짜 전류 = 0
⑺ Band 1은 전자로 꽉 차 있어 알짜 전류 = 0
⑻ Band 2와 3은 대칭성이 깨져야 알짜 전류가 존재
9. 응용 [목차]
⑴ 흑연이 전자가 흐르는 이유 : 마치 Na처럼 오비탈적으로 HOMO에서 LUMO로 전자가 쉽게 감
⑵ 전기전도도에 있어 Na이 Mg보다 큼 : 금속결합 → 오비탈이 하나의 띠
입력: 2019.09.08 21:15
'▶ 자연과학 > ▷ 일반화학' 카테고리의 다른 글
| 【화학】 9강. 기체 (2) | 2018.12.27 |
|---|---|
| 【화학】 8강. 물질의 상태 (0) | 2018.12.27 |
| 【화학】 6강. 양자역학 3부 - 오비탈 이론 (15) | 2018.12.27 |
| 【화학】 4강. 양자역학 1부 - 물질파의 도입 (0) | 2018.12.24 |
| 【화학】 3강. 원자가 전자쌍 반발 이론(VSEPR) (3) | 2018.12.20 |











최근댓글