5강. 양자역학 2부
추천글 : 【화학】 화학 목차
1. 슈뢰딩거 방정식 [본문]
2. 불확정성 원리 [본문]
3. 자유 입자 [본문]
4. 상자 속 입자 [본문]
5. 터널링 효과 [본문]
6. 유효질량 [본문]
7. 물질파의 반사 [본문]
8. 좌표계 변환 [본문]
9. 파동방정식의 해 [본문]
a. 양자역학 1부
b. 양자역학 2부
c. 양자역학 3부
d. 양자역학 4부
1. 슈뢰딩거 방정식(Schrödinger equation) [목차]
⑴ 가정 1. 파동함수 ψ = ψ(x, y, z, t)가 존재
① 코펜하겐 해석(Copenhagen interpretation) : | ψ(x) |2은 위치 x에서 전자를 발견할 확률 밀도를 의미
② 아인슈타인의 반박 : 전자의 위치는 결정돼 있으므로 확률로 정의하는 것은 부적절
③ 오랜 논쟁 끝에 코펜하겐 해석이 받아들여짐
⑵ 가정 2. ψ는 다음 방정식의 해가 됨 : 에너지 보존법칙

⑶ 가정 3. 시스템 변수의 값은 파동함수에 연산자를 작용함으로써 얻어짐

① α : 시스템 변수, αop : 수학적 연산자 (∂, ℏ, i 포함)
⑷ 슈뢰딩거 방정식 : 크게 두 가지 방정식으로 표현됨
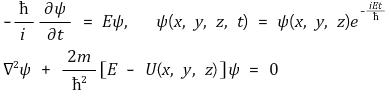
① 첫 번째 줄 : 에너지와 시간의 관계
② 두 번째 줄 : 에너지 보존 법칙
③ 시간 독립성 슈뢰딩거 방정식 : 총 E가 일정한 경우
④ 시간 의존성 슈뢰딩거 방정식 : 총 E가 시간에 따라 변하는 경우
⑤ 슈뢰딩거 방정식의 정확한 해를 구할 수 있는 것 : 단순 조화 진동, 1차원 상자 내 입자, 강체 회전, 수소 입자 등
⑥ 슈뢰딩거 방정식의 정확한 해를 구할 수 없는 것 : 헬륨 입자 등
2. 불확정성 원리(uncertainty principle) [목차]
⑴ 하이젠베르크(Werner Karl Heisenberg)가 발표
⑵ 증명 : 슈뢰딩거 방정식과 코시-슈바르츠 부등식 이용

⑶ 운동량과 위치를 동시에 정확하게 아는 것은 불가능
① 수식화
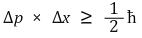
② (주석) 운동량은 공간에 대한 대칭성으로 도출된 개념으로 공간과 관련이 있음
③ 응용 : 불확정성 원리와 현미경

○ 파장이 λ인 광자의 운동량은 h/λ이기 때문에 λ가 감소하면 광자의 운동량은 커짐
○ 운동량이 크면 전자의 Δp 또한 커짐
○ 결론 : 현미경의 해상도를 높이기 위해 λ를 감소시키면 Δp가 커져서 오히려 운동량을 알기 어려워짐
⑷ 에너지와 시간을 동시에 정확하게 아는 것은 불가능
① 수식화
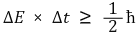
② (주석) 에너지는 시간에 대한 대칭성으로 도출된 개념으로 시간과 관련이 있음
⑸ 파속
① 주어진 영역에 국한된 고전적 입자의 양자역학적 개념
② 무리를 이루는 일정한 에너지의 파동함수 해들의 선형결합
③ 군속도(group velocity) : 여러 파동함수가 중첩된 경우의 속도 개념
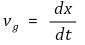
④ 분산관계(dispersion relationship)
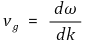
3. 자유 입자(free particle) : U = 0 [목차]
⑴ 결론 1. ψ는 파동방정식으로 유도
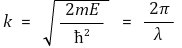
⑵ 결론 2. 운동량은 드 브로이(de Broglie) 관계식
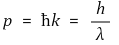
⑶ 결론 3. 에너지는 고전역학의 자유입자와 같음
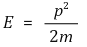
4. 상자 속 입자(particle in a box) : 일반적으로 1차원 상자 속 입자를 지칭 [목차]
⑴ 가정
① x < 0, x > L : 퍼텐셜에너지는 ∞
② 0 ≤ x ≤ L : 퍼텐셜에너지는 0
③ 입자는 물질파로 간주하며 정상파 조건, 즉 nλ = 2L을 만족
④ 파동함수가 시간에 대해 불변
⑵ 주요 공식
① 확률진폭함수
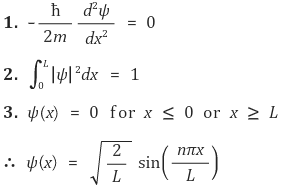
② 에너지
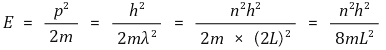
⑶ 예제 1. 폭이 L인 1차원 무한 퍼텐셜 우물에 갇힌 전자의 파동함수에서 확률의 규격화로부터 구한 진폭을 A라 할 때, 폭을 절반으로 줄인 우물의 파동함수 진폭은?
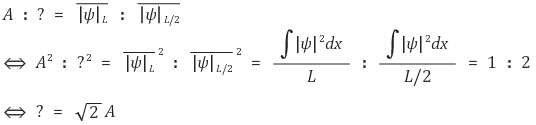
⑷ 예제 2. ψn(x)가 규격화된 n 번째 고유파동함수라 할 때, 다음 상태함수를 갖는 입자의 에너지는?
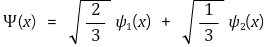
① 아이디어. 주어진 입자는 1번째 고유파동함수를 가질 확률이 2/3, 2번째 고유파동함수를 가질 확률이 1/3임
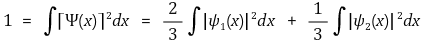
② 답. E = (2/3) × E2 + (1/3) × E2 = 2E2
5. 터널링 효과(tunneling effect) [목차]
⑴ 정의 : 입자성만 있다면 통과할 수 없는 장벽을 입자가 통과하는 현상
⑵ 슈뢰딩거 방정식을 풀면 유한 퍼텐셜 우물 밖에서도 입자를 찾을 확률이 있음
⑶ 터널링 효과 문제
① 문. 두께가 2 nm이고, 높이가 4 eV이 포텐셜 장벽에 에너지가 0.1 eV인 입자가 입사한다. 이 입자가 이 장벽을 투과할 확률은 T0이다. 동일 조건에서 장벽의 두께를 3 nm로 하였을 때, 입자가 장벽을 투과할 확률은?

② 답. 이 입자가 6 nm를 투과할 확률은 2 nm를 투과할 확률의 세제곱이고 3 nm를 투과할 확률의 제곱임

⑷ 응용 : 주사 터널링 현미경(STM, scanning tunneling microscope)

① 탐침이 P에 있을 때가 Q에 있을 때보다 퍼텐셜 장벽의 폭이 넓음
② 탐침이 P에 있을 때가 Q에 있을 때보다 전자가 탐침과 시료 사이를 이동할 확률이 적어짐 (∵ 폭이 넓어져서)
③ 탐침이 P에 있을 때가 Q에 있을 때보다 전류의 세기가 작아짐 (∵ 전자의 이동 확률이 적어져서)
④ 전류를 읽어서 시료의 표면 구조를 파악할 수 있음
6. 유효질량 [목차]
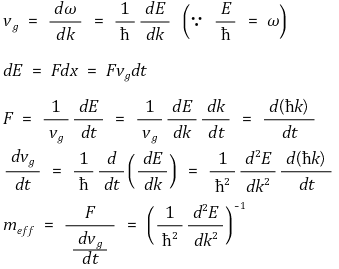
7. 물질파의 반사 [목차]
⑴ 전자기파의 반사 : 반사율 = 반사 전계 세기 ÷ 입사 전계 세기 (단, η = 고유 임피던스)
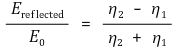
⑵ 물질파의 반사
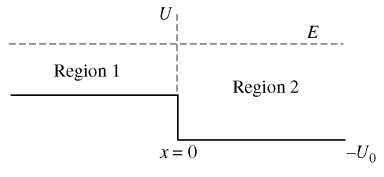
Figure. 5. 물질파의 반사 문제 상황
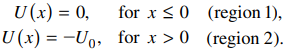
① 상황 1. E > 0인 입자 빔은 왼쪽에서 입사
② 상황 2. 각 영역에서 입자의 운동량은 ℏk으로 보존됨
③ x = 0에서의 반사율(reflection coefficient) R은 다음과 같음

8. 좌표계 변환(coordinate conversion) [목차]
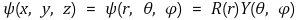
⑴ r : 원점으로부터의 거리
⑵ θ : z축으로부터의 각도 (위도)
⑶ φ : z축 주위로의 각도 (경도)
⑷ R(r) (radial wave funciton) : 오비탈의 크기를 결정
⑸ Y(θ, φ) (angular wave function) : 오비탈의 방향성, 분포 모양을 결정
9. 파동방정식의 해 [목차]
⑴ 양자화된 인자(= 양자수)가 정해지는 때만 파동함수가 도출
⑵ radial wave function의 해
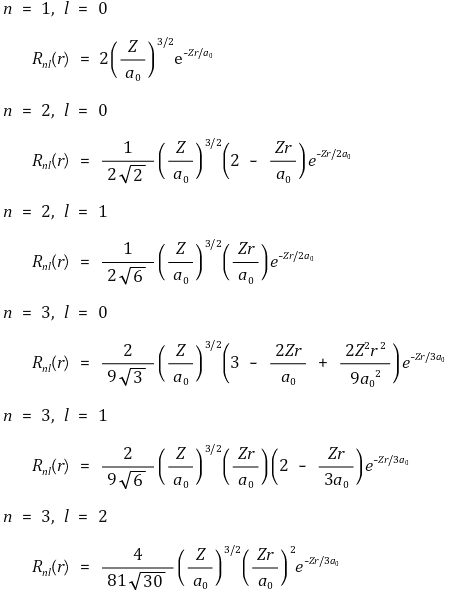
⑶ angular wave function의 해
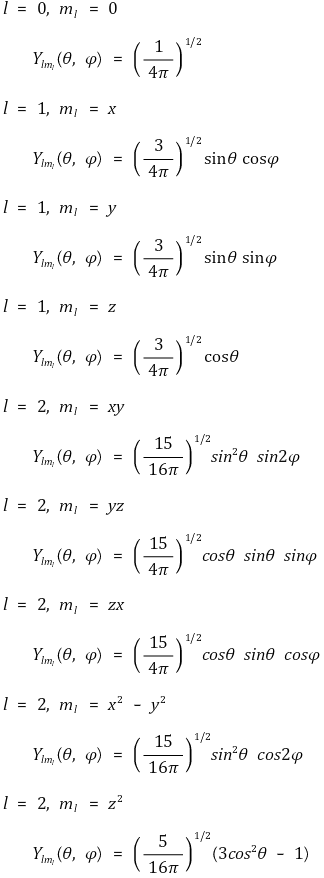
⑷ 각운동량 관계식
① 각운동량의 피타고라스 법칙
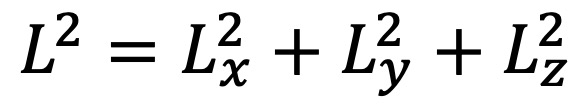
② 원자 내 전자의 각운동량 : 각운동량 양자수 ℓ에 대하여,
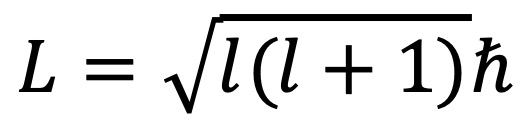
③ z축 각운동량의 결정 : 제이만 효과와 라모어의 세차운동
입력: 2019.09.08 21:04
수정: 2020.02.08 23:45
'▶ 자연과학 > ▷ 일반화학' 카테고리의 다른 글
| 【화학】 4강. 양자역학 1부 - 물질파의 도입 (0) | 2018.12.24 |
|---|---|
| 【화학】 3강. 원자가 전자쌍 반발 이론(VSEPR) (3) | 2018.12.20 |
| 【화학】 2강. 고전원자론 (0) | 2018.12.20 |
| 【화학】 1강. 화학의 기초 (0) | 2018.12.20 |
| 【화학】 백금 배위화합물 합성 (0) | 2016.06.25 |




최근댓글