추천글 : 【MRI 이론】 MRI 이론 목차
1. 자기장 [목차]
⑴ 정의 : 단위 면적당 자기선속, 크기와 방향을 갖는 벡터량으로 B로 표시
⑵ 발생 : 전하를 띤 입자의 운동이나 전류를 통해 발생

⑶ 방향 : 전하를 띤 입자의 운동 방향이나 전류 방향을 엄지손가락으로 하여 오른나선을 그리는 방향
⑷ 자기력 : 로렌츠힘(Lorenz force)이라고 불림

⑸ 자기 퍼텐셜 에너지(magnetic potential energy)

⑹ 전자기파의 발생 : 전기장과 자기장이 시간에 따라 변하는 경우
① 에너지 계산은 포인팅 벡터(Poynting vector) 개념을 사용
② 전자기파가 진공에서 존재할 수 있는 것은 전기장과 자기장이 상호유도를 하기 때문
③ MRI에서는 라디오 주파수(RF, radio frequency)가 사용
2. 핵 자기 모멘트 [목차]
⑴ 자기 (쌍극자) 모멘트(magnetic dipole moment or magnetic moment)
① 자기 쌍극자 : 막대자석과 같이 N극과 S극을 갖는 물질
② 전류가 흐르는 고리형 도선에서 토크 계산을 쉽게 하기 위해 도입
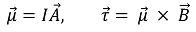
○ μ : 자기 모멘트
○ I : 전류
○ A : 면적 벡터
○ τ : 토크
○ B : 자기장
③ 자기 모멘트는 영구자석, 오비탈 전자, 전자 스핀, 핵 스핀 등에 적용할 수 있음
⑵ 각운동량과 자기 모멘트의 관계
① 일반적으로 자기장 B0의 방향을 z축으로 설정
② 각 양성자는 자기장을 축으로 세차운동(팽이운동)을 하기 시작 : 각운동량 발생
③ 양성자들의 세차운동의 방향은 B0에 나란할 수도 있고 반대일 수도 있음
⑶ 전체 각운동량과 전체 자기 모멘트와의 관계식
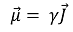
① 핵 스핀에 의한 양성자의 자전축과 자기 모멘트가 나란함
② μ : 전체 자기 모멘트
③ γ : 자기회전비율(gyromagnetic moment)
④ J : 전체 스핀 각운동량
⑷ 토크와 전체 각운동량의 유도식
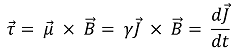
⑸ 원자의 자기 모멘트
① 종류 1. 전자의 궤도 운동에 의한 자기 모멘트
② 종류 2. 전자의 스핀에 의한 자기 모멘트
③ 원자의 자기 모멘트의 특징
○ 채워지지 않은 전자껍질 : 전자의 스핀이 원자의 자기 모멘트를 만듦
○ 채워진 전자껍질 : 자기 모멘트의 합은 0 (∵ 같은 수의 반대 스핀의 전자들로 채워지므로)
○ 채워지지 않은 최외각 전자껍질이 여러 개인 경우 : 다른 최외각 전자의 자기 모멘트와 상쇄됨. 훈트 규칙과 관련
○ 채워지지 않은 내부 전자껍질이 있는 경우 : 전자의 자기 모멘트가 거의 상쇄되지 않음 (예 : 전이 원소, 희토류)
3. 핵 스핀 [목차]
⑴ 원자의 구조
① 원자의 기본 구성 : 양성자, 중성자, 전자
② 양성자와 중성자는 핵을, 전자는 오비탈을 구성
③ 원자번호 : 원자 내 양성자 개수, 원소를 구분하는 기준
④ 원자량 : 원자 내 양성자와 중성자의 수의 합
⑤ 동위원소(isotope) : 원자번호는 같으나 원자량이 다른 원자. 똑같은 화학반응에 참가하지만 반응비가 다름
⑵ 스핀 각운동량
① 스핀 각운동량 : 고전적 해석에 따르면 스핀이 있는 핵은 자전축을 가지고 일정한 속도로 회전
② 스핀과 스핀 각운동량의 관계식
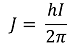
○ J : 스핀 각운동량
○ I : 스핀
○ 양자화 되어 있는 스핀양자수가 0이 아닌 화학종은 MRI에 사용될 수 있음
③ z축 자기모멘트

○ I : 스핀
○ m : 양자수. -I, -(I - 1), ···, (I - 1), I
○ γ : 자기회전비율(gyromagnetic ratio)
○ m : 양자수
④ I = 0
○ 원자량과 원자번호가 모두 짝수인 경우
○ 스핀의 알짜 자기모멘트가 0이므로 외부 자기장과 상호작용하지 않아 MR을 통해 분석할 수 없음
○ 스핀이 모두 cancel-out 됨
○ 예 : 12C (양성자 6개, 중성자 6개), 16O (양성자 8개, 중성자 8개)
○ Ar이나 Ce를 대부분의 원소들은 핵 스핀을 가지는 동위원소를 적어도 하나씩은 가짐
○ 따라서 원리적으로 거의 모든 원소가 MRI를 통해 분석될 수 있음
⑤ I = 정수(1, 2, ···)
○ 원자량이 짝수이고 원자번호가 홀수인 경우
○ 예 : 2H (양성자 1개, 중성자 1개), 6Li (양성자 3개, 중성자 3개)
⑥ I = 반정수(1/2, 3/2, ···)
○ 원자량이 홀수인 경우
○ 예 : 1H (양성자, proton)
⑶ 개념의 단순화
① 대부분 수소 원자(proton)가 MRI에 사용됨
○ 이유 1. 1/2의 스핀값을 가지고 있음
○ 이유 2. 자연상에서 가장 흔한 원소, 인체에도 풍부함
○ 이유 3. 외부 자기장에 반응하는 정도가 자연상에서 가장 큼 : 자기모멘트가 2.796 μn임
② 단순화
○ 핵의 스핀과 자기장의 상호작용을 기술하려면 복잡한 양자역학이 필요
○ 하지만 대부분의 MRI에서는 핵의 행동을 분석할 때 고전적인 접근만 이용 (그걸로도 충분하다는 의미)
4. 제이만과 라모어 [목차]
⑴ 개요
① 최초의 핵 자기 공명 연구는 Bloch과 Purcell에 의해 이루어짐
② 이후 이들은 1952년 노벨 물리학상을 수상
⑵ 제이만 효과(Zeeman effect)
① 외부 자기장에 의해 분자 스펙트럼에서 하나의 선이었던 에너지 준위들이 갈라지는 현상
② 에너지 준위의 관계식
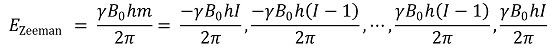
○ I : 스핀
○ m : 양자수. -I, -(I - 1), ···, (I - 1), I
○ γ : 자기회전비율(gyromagnetic ratio)
○ B0 : 외부 자기장
○ h : 플랑크 상수
③ 에너지 준위 차이
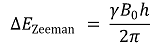
④ 에너지 준위 차이에 해당하는 라디오파를 입사하면 공명 흡수가 일어남
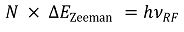
⑶ 라모어의 세차운동(Larmor precession)
① 거시계에서의 세차운동과 미시계에서 인접한 에너지 준위를 핵스핀이 끊임 없이 왔다갔다 하는 현상이 대응
② 플랑크 법칙과 제이만 효과를 결합하면, 세차운동의 주파수를 얻을 수 있음
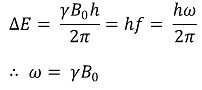
○ ω0 : 세차운동의 주파수(MHz)
○ B0 : 자기장 세기(T)
○ γ : 자기회전비율(gyromagnetic ratio). 단위는 MHz/T임
Figure. 1. 균일한 자기장 B0 하에 한 자기 모멘트의 라모어 세차운동
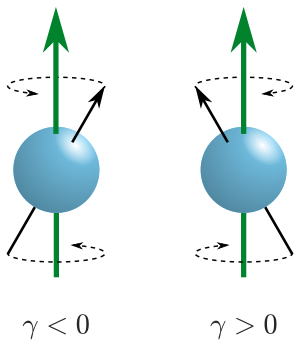
③ 핵스핀 방향 및 세차운동의 회전방향
○ μ × B = (1/γ) dμ / dt이고 proton을 비롯한 주요 핵 스핀의 γ가 γ > 0이므로 세차운동의 회전축 방향은 자기장에 대하여 시계방향
○ 수소와 같이 γ > 0인 경우 핵스핀 방향과 세차운동 방향이 다소 반대임을 유의
⑷ proton과 제이만 효과
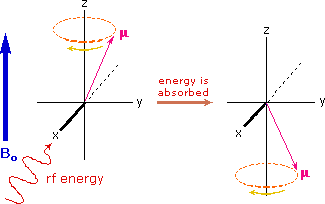
① proton의 z축 방향 자기모멘트는 2개 : B0와 나란한 방향(spin-up)과 반대 방향(spin-down)

② 자기장이 걸리면 spin-down이 spin-up보다 에너지 준위가 ΔE 만큼 높아짐
Figure. 2. spin-up이 에너지를 흡수하여 spin-down이 되는 과정
○ ΔE는 자기장의 세기 B0에 의존하고 양의 상관관계임
③ 볼츠만 분포에 따라 spin-up이 더 많아짐
Figure. 3. 외부 자기장 세기에 따른 spin-up과 spin-down의 에너지 준위 차이
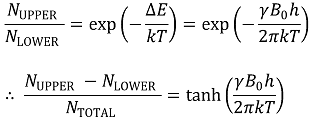
○ k : 볼츠만 상수, 1.381 × 10-23 JK-1
○ 예 1. 체온(310 K), 1 T에서 spin-up이 spin-down보다 0.34 ppm만큼 더 많음
○ 예 2. 체온(310 K), 1.5 T에서 조직 내 1025개의 양성자 중 ~1 : 106의 비로 spin-up이 훨씬 많음
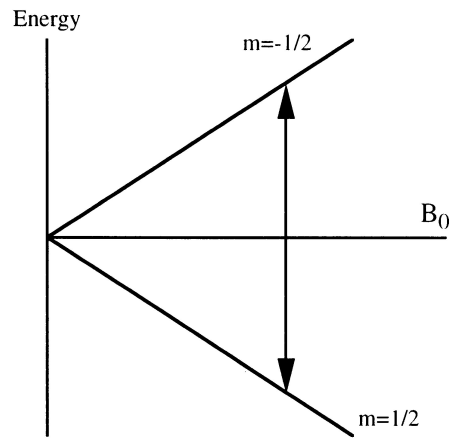
④ 결과적으로 z축의 양의 방향으로 알짜 자기모멘트가 형성 → 알짜 자화 M0 발생
Figure. 4. Zeeman diagram
⑸ 주요 핵스핀
Table. 1. 주요 핵 스핀
5. 자성체와 자화율 [목차]
⑴ 알짜 자화(net magnetization, bulk magnetization)
① 알짜 자화는 대부분 z축 자화이며, NUPPER - NLOWER에 비례하는 물리량
② 대부분의 물질에서 내부 편극 M0는 자기장 B0에 비례
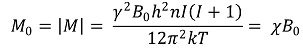
○ χ : 자화율(magnetic susceptibility)
○ 자화감수성 또는 자화율 : 외부 자기장이 놓였을 때 특정 물질이 자화되는 정도
③ MRI에서 직접 측정하는 물리량은 알짜 자화로, 자석의 세기를 측정하는 것과 비슷한 방법으로 측정
④ 자기장 세기 증가 → 알짜 자화 M0 증가 → MR 신호 증가
⑵ 자성체와 자화율
Figure. 5. 자성체의 분류
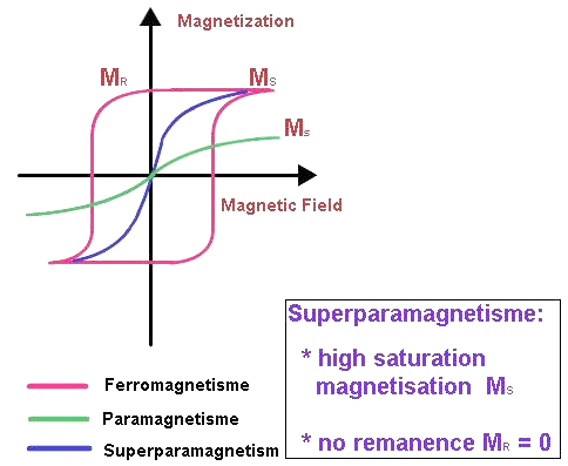
Figure. 6. 자성체와 자기이력곡선
① 반자성체(diamagnetic) : 초전도체를 제외하고는 χ의 값이 매우 작고 음수
○ 거시적 원인 : 외부 자기장의 반대 방향으로 물질 전체가 약하게 자화됨
○ 미시적 원인 : 모든 물질은 핵을 둘러싸는 전자의 운동 때문에 약한 반자성을 띰 (렌츠의 법칙)
○ 자기장 하에서 약한 척력을 발생
○ 초전도체 또한 반자성체의 예 (마이스너 효과)
② 상자성체(paramagnetic) : χ가 작고 양수
○ 거시적 원인
○ 외부 자기장이 없는 경우 : 자기 모멘트는 다시 무질서하게 배열됨
○ 외부 자기장이 있는 경우 : 외부의 자기장에 의해 일렬로 정렬되어 약한 인력 형성 (∵ 토크로 인한 회전)
○ 약한 인력을 형성하는 이유 : 원자들의 열운동으로 자기 모멘트의 정렬이 흐트러지기 때문
○ 상자성체의 온도를 낮추어 원자들의 열운동을 약화시키면 상자성체는 강하게 자기화됨
○ 미시적 원인
○ MO theory에서 홀전자를 가지고 있는 분자들에서 나타남
○ 즉, 채워지지 않은 전자껍질을 가지는 분자들에서 나타남
○ 예 : 전이 원소, 희토류 원소, 악티늄 계열 원소
③ 강자성체 : χ가 매우 크고 양수
○ 거시적 원인
○ 강자성 물질 내부는 자기구역(magnetic domain)로 나뉘어져 있음
○ 교환 결합 : 한 원자의 전자 스핀이 인접한 다른 원자의 전자 스핀과 상호 작용
○ 원자들의 열운동에도 불구하고 교환결합에 의해 특정 자기구역 내의 자기 모멘트는 같은 방향으로 정렬돼 있음
○ 외부 자기장이 없는 경우 : 각 자기 구역의 자기 모멘트가 무질서하므로 전체 자기장을 띠지 않음
○ 외부 자기장이 있는 경우 : 각 자기구역의 자기 모멘트가 외부 자기장 방향으로 정렬됨 (∵ 토크로 인한 회전)
○ 외부 자기장이 제거된 경우 : 각 자기구역의 자기 모멘트가 무질서해지지 않고 자기화가 오래 유지됨
○ 금속성 물질에서 주로 발견 : 철, 코발트, 니켈, 가돌리늄, 산화철 등
○ 강자성체를 ferro-magnetic, ferri-magnetic, antiferro-magnetic 등으로 세분화하기도 함
○ 쿼리 온도(Curie temperature)
○ 강자성체의 온도가 임계 온도 이상이 되면 교환 결합이 끊어져서 더 이상 자기구역의 정렬을 유지할 수 없음
○ 이 온도 이상에서는 원자의 열운동이 매우 커서 강자성체가 강자성을 잃고 상자성체가 됨
○ 이 온도를 퀴리 온도라고 함
| 강자성체 | 퀴리 온도(K) |
| 철 | 1043 |
| 코발트 | 1394 |
| 니켈 | 631 |
| 가돌리늄 | 317 |
| 산화철 (Fe2O3) | 893 |
Table. 2. 여러 물체의 퀴리 온도
○ 번개 유도 전류 자기(lightning-induced remanent magnetism)
○ 번개가 치면 주변의 자철석이 자기화되어 자석이 되는 현상
○ 천연 자석이 생성되는 메커니즘
○ 자기이력현상(magnetic hysteresis) : 강자성 물질 특유의 현상
○ 이력현상(hysteresis) : 물질의 물리량이 현재의 상태뿐만 아니라 상태의 변화 과정에 의하여 결정되는 현상
○ 이력현상은 자기이력현상만 있는 것은 아님
○ 예 : 응력-변형률 곡선의 이력현상, 함수율 이력현상
○ 강자성체의 자기장을 B, 외부 자기장을 H라고 표현
○ (참고) B = μH로 표현되어 외부 자기장의 단위가 강자성체의 자기장의 단위와 다름
○ 자기 이력 곡선(hysteresis loop) : 강자성체 혹은 초상자성체의 자기장이 외부 자기장 변화에 따라 변하는 과정을 묘사한 곡선
Figure. 7. 자기 이력 곡선 또는 히스테리시스 곡선
○ 1st. 초기 자기화 곡선 (O → D)
○ 자기화되지 강자성체에 외부 자기장을 가하면 초반에는 강자성체의 자기장이 급격하게 증가함
○ 자기장이 급격하게 증가하다가 점점 증가속도가 감소하여 더 이상 자기장이 증가하지 않음
○ 강자성체의 각 자기구역들은 외부 자기장과 완전히 동일한 방향으로 정렬됨
○ 자기 포화(magnetic saturation) : 외부 자기장을 증가시켜도 강자성체의 자기장이 더 증가하지 않는 현상
○ 2nd. 외부 자기장의 세기가 감소할 때 (D → E)
○ 강자성체의 자기구역이 처음 상태로 돌아가지 않고 어느 정도 정렬된 상태를 유지함
○ 따라서 자기 이력 곡선은 O로 돌아가지 않음
○ 잔류 자기장 : E 지점에서의 자기장
○ 3rd. 반대 방향의 외부 자기장을 가할 때 (E → F → G)
○ F 지점 : 강자성체의 자기장은 더욱 감소하여 0이 됨
○ F 지점에서의 외부 자기장을 보자력(coercive force, coercivity) 또는 항자력이라고 함
○ 반대 방향의 외부 자기장의 세기를 더욱 증가시키면 자기구역이 외부 자기장 방향으로 재정렬하여 포화됨
○ 4th. 반대 방향의 외부 자기장이 감소하고 다시 처음 자기장을 가할 때
○ J를 지나 다시 D 상태로 돌아옴
○ VSM(vibrating sample magnetometer)에 의해 측정됨
○ 응용 1. 영구 자석 : 외부 자기장이 없어도 자기장을 유지 → 자기 이력 곡선이 사각형이고 보자력이 커야 함
○ 응용 2. 전자석 또는 변압기에 쓰이는 철심 : 외부 자기장에 민감하게 반응 → 잔류 자기장은 크고 보자력이 작음
○ 강자성체는 반자성체, 상자성체와 달리 MRI에 심각한 artifact를 일으킴
④ 자성체별 특성 요약
| 자성체 | 내부 자화의 방향 | 자화율 (χ) | 예시 |
| diamagnetism | 외부 자기장과 반대 | -10 ppm | 물, 지방, 칼슘, 대부분의 조직 |
| paramagnetism | 외부 자기장과 동일 | +1 ppm | 산소 분자, 염, 킬레이트 금속 (Gd, Fe, Mn, Cu), organic free radical |
| superparamagnetism | 외부 자기장과 동일 | +5000 ppm | ferritin, hemosiderin, SPIO 조영제 |
| ferromagnetism | 외부 자기장과 동일 | > 10,000 | iron, steel |
Table. 3. 자성체별 특성 요약
⑶ 초전도체(superconductor)
① 개요
○ 정의 : 특정 온도 이하에서 전기 저항이 0이 되는 물질
○ 1956 ~ 57년에 이론적으로 설명
○ 예 : 수소 기체를 많이 압축해서 고체로 만들면 초전도체가 됨
② 쿠퍼쌍(Cooper pair)
○ 1956년 Leon Cooper에 의해 처음으로 제안됨
○ 1st. 일반적으로 전자 간 상호작용은 반발력을 야기함
○ 2nd. 전자가 이동할수록 전자의 길을 구성하는 lattice가 양하전을 띠어 electron-phonon interaction이 일어남
○ 3rd. 온도가 낮아지면 electron-phonon interaction의 영향이 드러나기 시작함
○ 4th. 한 쌍의 전자(스핀 : ±1/2)가 Cooper pair를 형성하며 스핀이 정수인 보존(boson)과 같이 행동
○ 5th. 전자 간에는 같은 양자 상태(quantum state)를 가질 수 없지만 (∵ 파울리 배타 원리), boson-like는 가능함
○ 6th. Bose-Einstein condensate : Cooper pair가 모두 같은 양자 상태를 가지며 하나의 entity처럼 행동 :
○ 7th. Cooper pair는 scattering 없이 유동을 하게 됨
○ 8th. 전기 저항이 0이 됨
○ 쿠퍼쌍 개념은 초전도체뿐만 아니라 헬륨의 초유동(superfluidity, 저항이 0인 유체) 등에도 적용 가능
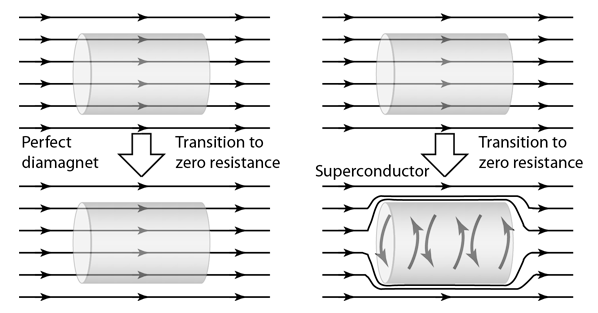
③ 마이스너 효과(Meissner effect)
○ 정의 : 초전도체가 외부 자기장을 밀어내는 현상. 즉, 초전도체 또한 반자성체
Figure. 8. 마이스너 효과
○ 예 : 초전도체 위에 자석이 뜨는 현상, 자기부상열차
④ 고온 초전도체
○ 1986년 임계 온도가 28 K인 초전도체를 발견
○ 현재 임계 온도가 150 K인 초전도체를 발견
○ 고온 초전도체는 초전도 현상을 실용화하는 데 매우 중요한 역할을 수행
⑤ 예 1. Y-Ba-Cu-O [YBCO] 초전도체
○ 92 K (-181 ℃) 근처의 임계온도를 가짐
○ 액체 질소를 이용해 77 K (-196 ℃)까지 온도를 낮추면 마이스너 효과 발생
⑥ 예 2. Bi-Sr-Ca-Cu-O [BSCCO] 초전도체
○ 110 K (-163도) 근처의 임계온도를 가짐
○ 액체 질소를 이용해 77 K (-196 ℃)까지 온도를 낮추면 마이스너 효과 발생
⑷ 자성체의 활용
① 전자석의 철심
② 하드 디스크
③ 고무 자석
④ 자동판매기의 동전 감별기
⑤ 캡슐형 내시경
⑥ 액체 자석
⑦ MRI : 초전도체 활용
⑧ 자기부상열차 : 초전도체 활용
⑨ 양자컴퓨터 : 초전도체 활용
⑩ 무손실송전 : 초전도체 활용
6. MRI [목차]
⑴ 1980년대 : MRI가 임상으로 사용되기 시작
⑵ 1988년 : 최초로 Gd-DTPA가 조영제로 사용됨
입력: 2017.03.02 16:11
수정: 2022.10.13 02:34
'▶ 자연과학 > ▷ 영상의학' 카테고리의 다른 글
| 【MRI 이론】 2강. 자기공명의 개념 (0) | 2022.12.08 |
|---|---|
| 【MRI 이론】 13강. MRS(Magnetic Resonance Spectroscopy) (0) | 2022.10.31 |
| 【MRI 이론】 MRI 이론 목차 (43) | 2022.04.29 |
| 【MRI 이론】 6강. 펄스 시퀀스 (2) | 2021.09.04 |
| 【MRI 이론】 17강. 임상적 적용 (0) | 2021.08.29 |








최근댓글