4강. 인장과 압축(stress and strain)
추천글 : 【재료역학】 재료역학 목차
1. 응력 [본문]
2. 축 방향 응력 계산 [본문]
3. 부하-변형 곡선 [본문]
4. 여러 가지 응력 [본문]
1. 응력 [목차]
⑴ 최소의 전단저항을 갖는 매질에서 작용
⑵ 매질을 손에 대고 반대 방향으로 비틀 때 손이 느끼는 저항
⑶ 종류 1. 변형력 : 변형(strain)에는 탄성 변형, 비탄성변형(= 연성 변형(늘려짐) + 취성 변형(깨짐))이 있음
⑷ 종류 2. 수직응력 : 면에 수직으로 작용. 양의 응력과 음의 응력이 있음
⑸ 종류 3. 전단응력 : 나란하게 작용
2. 축 방향 응력 계산 [목차]
⑴ 인장, 압축
Figure. 1. 축 방향 응력 계산
⑵ 수평면 내에서 회전하는, 두께가 얇은 링에 생기는 인장응력
Figure. 2. 수평면 내에서 회전하는, 두께가 얇은 링에 생기는 인장응력

3. 부하-변형 곡선(strain-stress curve) [목차]
⑴ 개요
① 부하-변형 곡선
○ 가로축 : 변형률(strain)
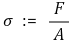
○ 세로축 : 응력(stress)
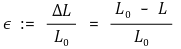
○ 아래 면적 : 에너지
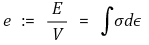
② 압축실험장치
○ 부하-변형 곡선은 일반적으로 인장실험보다 압축실험을 통해 얻어짐
○ 압축실험장치로 일반적으로 만능인장압축시험기( UTM, universal testing machine)이 사용됨
Figure. 4. 압축실험장치의 구성도
○ 단단한 시료 : 크로스헤드의 하강속도를 1.23 mm/min ± 50% 정도로 설정
○ 무른 시료 : 크로스헤드의 하강속도를 2.5-30 mm/min ± 50% 정도로 설정
⑵ 탄성영역(elastic region)
① 정의 : 탄성에 의해 복원할 수 있는 변형률 범위
② 비례한도(limit of proportionality)
○ 정의 : 훅의 법칙이 성립하는 변형률 범위
○ 훅의 법칙(Hooke's law) : σ = Eε. σ : 응력. E : 탄성계수. ε : 변형률
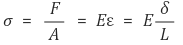
○ 탄성계수(영률, modulus of elasticity, Young's modulus)
○ 0 ~ 비례한도까지의 기울기로 일정한 값을 가짐
○ 단단한 물체일수록 E 값이 크고 변형이 어려움
○ 겉보기 탄성계수(apparent modulus of elasticity)
○ 이니셜 탄젠트 모듈러스(initial tangent modulus) : 원점에서의 접선기울기
○ 시컨트 모듈러스(secant modulus) : 원점을 지나는 직선의 평균기울기
○ 탄젠트 모듈러스(tangent modulus) : 임의의 점에서의 접선의 기울기
○ Hertz의 접촉이론에서 유도된 탄성계수 식

○ 탄성도(degree of elasticity)
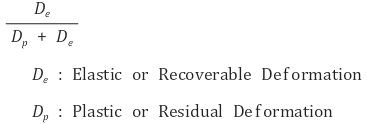
○ 레질리언스(resilience) : 응력-변형률 곡선에서 비례한도까지의 아래 면적. 변형 에너지의 척도 중 하나
○ 비례한도가 정의되지 않는 경우 항복지점까지의 면적으로 정의하기도 함
○ 예제
○ 수평 강체 빔 ABCD는 수직 바 BE와 CF에 의해 지지되며, 각각의 점 A와 D에서 수직 힘 P1 = 400 kN과 P2 = 360 kN이 작용하고 있습니다(도표 참조). BE와 CF 바는 강철(E = 200 GPa)로 만들어졌으며, 단면 면적은 BE = 11,100 ㎟, CF = 9,280 ㎟입니다. 바들의 다양한 점 사이의 거리는 도표에 표시되어 있습니다. 점 A와 D의 수직 변위 δA와 δD를 결정하십시오.
Figure. 5. 예제

③ 항복지점(yield point)
○ 탄성영역이 끝나는 지점 : 항복지점 이후에는 미세한 파괴가 시작하여 원 상태로 돌아오지 못함
○ 하중이 일시적으로 증가하지 않는 지점
○ 거침성(roughness) : 항복지점까지 필요한 에너지
○ 강직도(stiffness) : 0 ~ 항복지점까지의 평균 기울기
○ 항복변형량(yield deformation) : 0 ~ 항복지점까지의 변형량
④ 이력현상(hysteresis)
○ 이력현상 : 물질의 물리량이 현재의 상태뿐만 아니라 상태의 변화 과정에 의하여 결정되는 현상
○ 응력-변형률 곡선의 이력현상 : 항복지점 이상의 변형을 가하면 부하를 제거해도 원래 상태로 회복되지 않는 현상
○ 기계적 이력(mechanical hysteresis) : 하중을 loading할 때 흡수한 일량 - 그 뒤 하중을 unloading할 때 방출된 일량
○ 기계적 이력은 변형에너지(strain energy)를 열로 확산시키는 척도로서 단위체적당 일량 J/m3으로 표시
○ 이력손실(hysteresis loss) : 하중을 loading할 때 흡수한 일량에 대한 기계적 이력의 비. 백분율로 표시
⑶ 소성영역(plastic region)
① 정의 : 탄성에 의해 복원할 수 없는 변형률 범위
② 탄성 및 비탄성 변형에너지
○ 탄성한도 이내 : 전체 에너지가 복원됨
○ 탄성한도를 넘어서는 변형 : 새로운 탄성 구간에 대한 에너지만 복원됨
Figure. 6. 탄성 및 비탄성 변형에너지
③ 파단(rupture, fracture)
○ 정의 : 물체가 완전히 파괴되는 지점
○ 견고도(toughness) : 최종 파단 지점까지 필요한 에너지
○ 파단변형량(rupture of deformation) : 0 ~ 최종 파단 지점까지 필요한 변형량
○ 파단강도(fracture strength) : 파단 시 재료에 가해진 응력
④ 극한응력(ultimate stress) : 항복지점에서 최종 파단 지점까지 중 응력의 극대값
○ 일반적으로 최종 파단 지점의 응력을 지칭함
○ 강도(strength) : 물체의 극한응력
⑤ 연성과 취성 : 정도의 차이
○ 연성(ductility) : 항복지점 이후 최종 파단 지점까지 변형률이 많이 필요한 물성
○ 연성 물질이 파괴될 때 파괴면이 많이 변형
○ 취성(brittleness) : 항복지점 이후 최종 파단 지점까지 변형률이 적게 필요한 물성
○ 취성 물질이 파괴될 때 파괴면이 거의 변하지 않음
⑷ 피로(fatigue)
① 정의 : 파단응력 이하의 응력이 지속적으로 가해져도 일정 시간 후 재료가 파괴되는 현상
② 반복피로(cyclic fatigue)
③ 점탄성이 있는 물질은 응력-하중의 관계가 시간에 따라 변화
○ 리올로지 모델로 설명
○ 응력이완(stress relaxation) : 변형률이 일정할 때 응력이 감소하는 현상
○ 크리프 현상(creep phenomenon) : 항복점 이하의 작은 하중에도 작용시간이 길어지면 손상이 발생하는 현상
⑸ 포아송 비(푸아송 비, Poisson's ratio)
① 정의 : 가로 변형률을 세로 변형률로 나눈 값
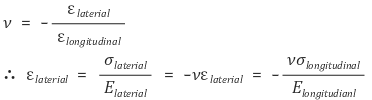
○ 푸아송 비는 항상 양의 값
○ 결정구조에 따라 값이 결정
○ 포아송 비는 항상 0.5보다 작음
○ 금속의 경우 일반적으로 1/3
② 단면적의 변화율 : 포아송 비 ν에 대하여,
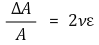
③ 체적변화율 : 중첩의 원리(superposition's law)를 통해 얻어짐
○ 수식화

○ 충분히 특정 단면의 결정구조를 확장하여 체적 변형률 εV를 결정할 수 있음
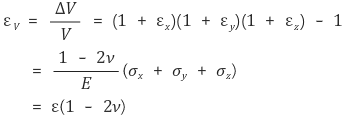
○ 체적 변형률 εV는 대략 다음과 같이 표현할 수도 있음
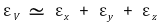
○ 팽창을 시켰을 때 부피변화율이 음일 수 없음
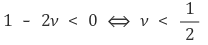
○ 단, 고무는 포와송의 비 ν의 값이 0.5이므로 체적의 변화가 없음
④ 세로 탄성 계수 E와 가로 탄성 계수 G의 관계식
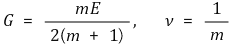
4. 여러 가지 응력 [목차]
⑴ 편심하중을 받는 단주
① 최대 응력 : 참고로 M은 무게중심에 대한 모멘트임
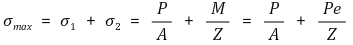
② 최소 응력 : 참고로 M은 무게중심에 대한 모멘트임
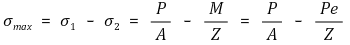
③ 핵심거리 : 최소 응력이 0이 되는 편심거리 e를 지칭함
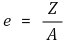
⑵ 장주
① 오일러의 좌굴하중 : 임계하중, 안전하중이라고도 함
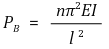
○ n : 단말계수. 이 값이 클수록 강한 기둥
○ ℓ : 기둥의 길이. 이 값이 클수록 약한 기둥
○ (주석) EI는 대부분 붙어 다님
② 오일러의 좌굴응력
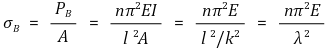
○ k : 회전반경 (최소 단면 2차 반경)
○ λ : 세장비
③ 좌굴세장비 : 유효세장비라고도 함
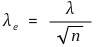
⑶ 열응력(thermal stress)
① 열팽창
○ 부재의 온도가 증가하면 모든 방향으로 길이가 증가 : 운동에너지 상승 때문
○ 선팽창 계수가 α이고 온도 변화가 ΔT일 때 선형 물체의 늘어난 전체 길이 ℓ = ℓ0 (1 + α ΔT)
○ 부피팽창 계수가 β이고 온도 변화가 ΔT일 때 물체의 늘어난 전체 부피 V = V0 (1 + β ΔT)
○ β ≒ 3 α가 성립 : 1 + β ΔT = (1 + α ΔT)3 ≒ 1 + 3α ΔT (증명)
○ 열팽창 계수 : Zn, Pb, Mg > W, Mo > V
② 열응력 : 부재가 열팽창하지만 두 점 간의 거리가 변할 수 없는 경우 응력이 발생
Figure. 7. 열에 의한 응력
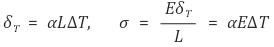
⑷ 충격 응력(impulse stress)
① 수식화 : 팁. 암기해야 함
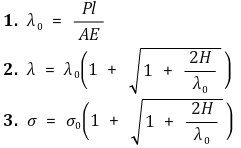
② 초속도 없이 급격히 힘을 가하면 σ = 2σ0 : 위 수식에서 H = 0을 대입하면 됨
⑸ 부정정
① 예제
○ 도표에 나타난 축방향으로 부하가 가해진 바 ABCD는 강한 지지대에 의해 고정되어 있습니다. 이 바는 A에서 C까지 단면적이 A1이고, C에서 D까지 단면적이 2A1입니다. 바의 끝 부분에서의 반력 RA와 RD를 결정하십시오.
Figure. 8. 부정정 예제
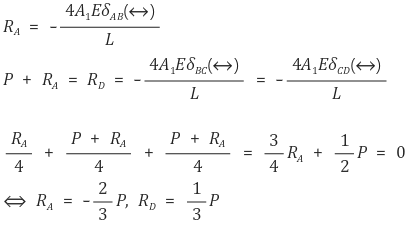
입력: 2016.04.24 16:32
수정: 2020.06.30 21:33
'▶ 자연과학 > ▷ 재료역학·고체역학' 카테고리의 다른 글
| 【재료역학】 7강. 비틀림 (0) | 2020.06.30 |
|---|---|
| 【재료역학】 6강. 모어 원 (0) | 2020.06.30 |
| 【재료역학】 3강. 하중 (0) | 2020.06.30 |
| 【생체재료】 3강. 생체역학 2부 (0) | 2019.12.01 |
| 【생체재료】 1강. 생체재료의 개요 (0) | 2019.11.29 |












최근댓글