6강. 모어 원(모아 원, Mohr's circle)
추천글 : 【재료역학】 재료역학 목차
1. 2차원상의 모아 원 [본문]
2. 3축 응력 [본문]
1. 2차원상의 모아 원 [목차]
⑴ (참고) 응력 요소

Figure. 1. 응력 요소
⒜ 3차원 형상의 응력 표시
⒝ 2차원 단면의 응력 표시
⒞ 기울어진 2차원 단면의 응력 표시
① ⒝에서 대칭성에 의해 좌측면의 전단응력 = 우측면의 전단응력 = τxy
② ⒞에서 대칭성에 의해 좌측면의 전단응력 = 우측면의 전단응력 = τx1y1
③ ⒝에서 모멘트 평형에 의해 전단응력이 같음 : τxy = τyx
④ ⒞에서 모멘트 평형에 의해 전단응력이 같음 : τx1y1 = τy1x1
⑤ ⒝에서 힘 평형에 의해 수직응력이 같음 : 좌측면의 수직응력 = 우측면의 수직응력 = σx
⑥ ⒞에서 힘 평형에 의해 수직응력이 같음 : 좌측면의 수직응력 = 우측면의 수직응력 = σx1
⑵ 절단면에 작용하는 응력

Figure. 2. 절단면에 작용하는 응력
① 절단면의 법선방향에 대한 평형조건
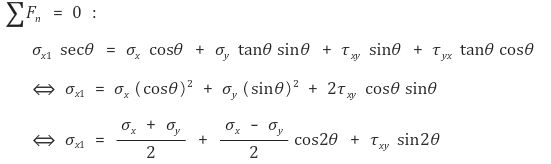
② 절단면의 접선방향에 대한 평형조건
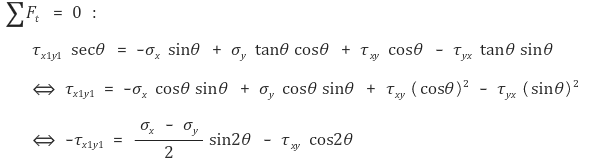
③ 결론 : 다음과 같은 원의 방정식을 찾을 수 있음
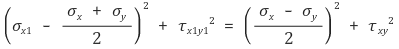
④ 주평면 : 최대, 최소 응력이 존재하고 전단력이 0인 단면
⑶ 모어 원 그래프 도식

Figure. 3. 모어 원 그래프 도식
① 반지름의 제곱이 (0.5σx - 0.5σy)2 + τxy2이고 중심이 (0.5σx + 0.5σy, 0)인 원의 방정식
② 양의 x축으로부터 θ 각을 이루는 x1 - y1 평면 위에 작용하는 응력 σx1과 τx1y1은 모어 원에서 σx1 축으로부터 반시계 방향으로 2θ 회전한 원주상의 좌표임
③ 해석 1. θ = 0일 때 수직응력은 최대이고 전단응력은 최소임 (자명)
④ 해석 2. ± 45°에서 τx1y1의 절댓값이 최대이므로 ± 45°를 따라 전단면이 형성
⑷ 스트레인 로제트(strain rosette)
① 일반식

Figure. 4. 스트레인 로제트
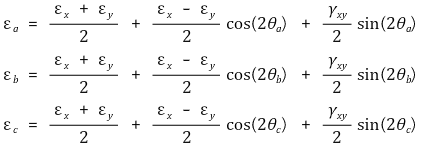
② 스트레인 로제트 - 45°

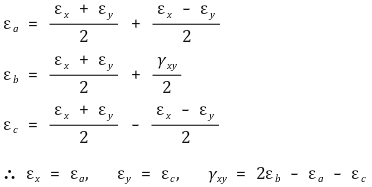
③ 스트레인 로제트 - 60°

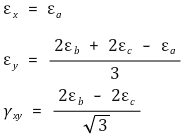
2. 3축 응력 [목차]
⑴ 예제 1. τp가 없다고 가정
① 4면체의 응력 요소

Figure. 7. 4면체의 응력 요소
② 전단응력 표시

Figure. 8. 전단응력 표시
(단, l, m, n은 방향 코사인(direction cosine))
○ x축에 대한 모멘트 평형에 의해 전단응력이 같음 : τzy = τyz
○ y축에 대한 모멘트 평형에 의해 전단응력이 같음 : τzx = τxz
○ z축에 대한 모멘트 평형에 의해 전단응력이 같음 : τyx = τxy
③ 기본 방정식
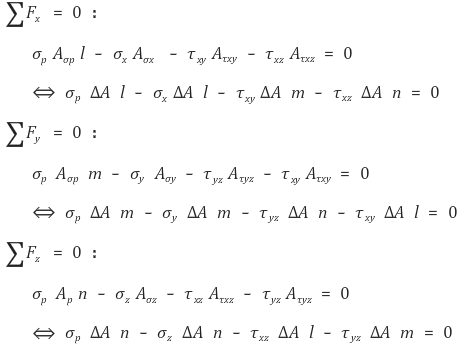
④ 행렬표현
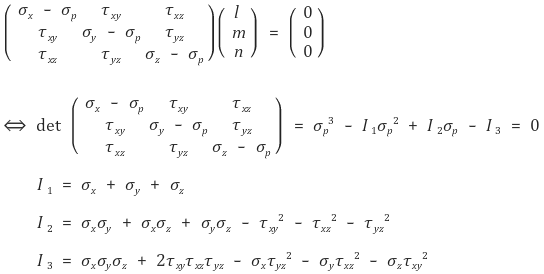
⑵ 예제 2. 외부 전단응력이 없다고 가정
① 조건 수식화
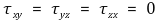
② 기본 방정식 : 힘의 평형 도입

③ τp를 다음 조건을 만족하는 τ1과 τ2로 분해
○ τ1은 (-m, l, 0)에 평행 : (l, m, n)과 수직
○ τ2는 (-n, 0, l)에 평행 : (l, m, n)과 수직
○ 발상 : σp가 (l, m, n)에 평행한 상황에서 x축, y축, z축에 대한 각 힘의 평형식에서 σp ΔA에 붙는 계수가 각각 l, m, n
○ 식의 재구성
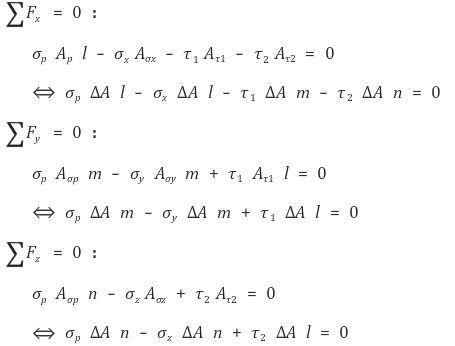
○ 결과
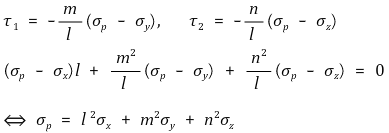
④ 그래프 도식 : 가로축을 σp, 세로축을 τp라고 할 때
○ l = 0인 경우 : 원의 방정식
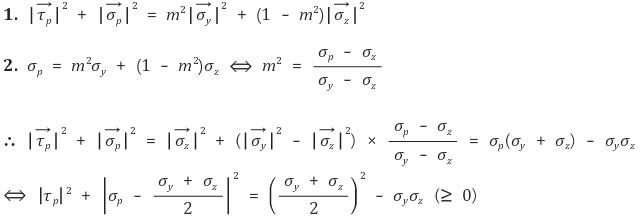
○ m = 0인 경우 : 원의 방정식
○ n = 0인 경우 : 원의 방정식
○ 종합적인 상황

Figure. 9. 종합적인 상황
○ 전략 : l = 0, m = 0, n = 0 각각에 대해 원을 따로 그림
○ 총 네 개의 영역으로 구분 : 편의상 위쪽을 영역 1, 왼쪽을 영역 2, 오른쪽을 영역 3, 아래쪽을 영역 4로 정의
○ Lemma. 종합적인 상황에서 모든 점은 영역 1 또는 영역 4에 놓임
⑤ Lemma의 증명
○ 우선 l ≥ 0, m ≥ 0, n ≥ 0에 대해서만 생각
○ 내부 점의 존재성 : 당장 P2라는 점이 대응되는 상황이 있음
○ 각각의 원 위에 점이 있는 경우 : l, m, n 중 하나는 0이어야 함
○ 가장 큰 원의 밖에 점이 있는 경우
○ Figure. 6.에서 가장 큰 원을 통과하지 않고 l, m, n의 값을 바꿔서 P2로 도달할 수 있는 경로는 없음
○ P2 근처의 점으로 이동하는데 l = 0, m = 0, 또는 n = 0이 되지 않도록 방향벡터 (l, m, n)의 경로를 설정하는 것은 가능
○ 따라서 가장 큰 원의 밖에 점이 있는 경우는 존재하지 않음
○ 왼쪽 원 안에 점이 있는 경우 : P1 근처의 점에 대해서 비슷한 논리를 적용할 수 있음
○ 오른쪽 원 안에 점이 있는 경우 : P3 근처의 점에 대해서 비슷한 논리를 적용할 수 있음
○ 연속성에 의해서 l ≥ 0, m ≥ 0, n ≥ 0이 아니어도 적용 가능
○ 엄밀하지 못한 서술
○ l ≥ 0, m ≥ 0, n ≥ 0이라 해도 영역 1 + 영역 4를 모두 덮지 못함
입력: 2016.05.30 11:21
'▶ 자연과학 > ▷ 재료역학·고체역학' 카테고리의 다른 글
| 【재료역학】 8강. 굽힘 (0) | 2020.06.30 |
|---|---|
| 【재료역학】 7강. 비틀림 (0) | 2020.06.30 |
| 【재료역학】 4강. 인장과 압축 (0) | 2020.06.30 |
| 【재료역학】 3강. 하중 (0) | 2020.06.30 |
| 【생체재료】 3강. 생체역학 2부 (0) | 2019.12.01 |




최근댓글