8강. 굽힘(bending)
추천글 : 【재료역학】 재료역학 목차
1. 미분방정식의 유도 [본문]
2. 최대 굽힘 응력 [본문]
3. 카스틸리아노의 정리 [본문]
1. 미분방정식의 유도 [목차]
⑴ 가정 1. θ가 충분히 작음

⑵ 가정 2. curvature-bending moment relationship : 빔이 linearly elastic할 때 만족하는 특성

⑶ deflection curve의 미분방정식
Figure. 1. deflection curve의 미분방정식

⑷ 원리 1. 부호 정의
Figure. 2. 빔의 굽힘 문제에 있어서의 부호 정의
⑸ 원리 2. 모멘트 M, 전단력 V, 분포하중 q에 대하여
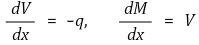
① 면적-모멘트법을 사용하여 처짐량 δ를 결정할 수 있음
② 공액 보 : 굽힘 모멘트 선도의 면적을 하중으로 생각한 보
③ (참고) 단순 굽힘 상태 : 모멘트 변화가 없는 구간
⑹ 원리 3. 연속(continuity) : 임의의 지점에서의 처짐량과 처짐 각도(dV/dx)는 연속이어야 함
⑺ 원리 4. 대칭성(symmetry)
⑻ 원리 5. 중첩의 원리 : 복합적 하중에 의한 처짐량은 각각의 하중별로 계산한 처짐량의 합과 같음
⑼ 종합
① 모멘트가 걸리는 외팔보 (캔틸레바) : 팁. θ 식의 계수는 1!와 관련. δ = ∫ L dθ = ∫ L (∂θ/∂L) dL로 외울 것
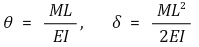
② 집중하중이 걸리는 외팔보 (캔틸레바) : 팁. θ 식의 계수는 2!와 관련. δ = ∫ L dθ = ∫ L (∂θ/∂L) dL로 외울 것
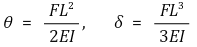
③ 분포하중이 걸리는 외팔보 (캔틸레바) : 팁. θ 식의 계수는 3!와 관련. δ = ∫ L dθ = ∫ L (∂θ/∂L) dL로 외울 것

Figure. 3. 외팔보에 분포 하중이 작용하는 경우
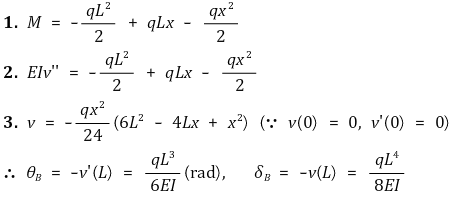
④ 집중하중이 걸리는 지지보 : 팁. 면적-모멘트법을 이용하면 됨
⑤ 분포하중이 걸리는 지지보 : 팁. 면적-모멘트법을 이용하면 됨
2. 최대 굽힘 응력 [목차]
⑴ 수식화

① M : 최대 굽힘 모멘트
② I : 면적 관성모멘트
③ c : 단면상에서 축으로부터 가장 먼 거리
④ S : 단면계수. 이 값이 클수록 굽힘에 강함
⑵ 응용
① 정방향 단면의 보가 원형 단면의 보보다 큰 하중을 견딜 수 있음
⑶ 전단응력
① 수식화
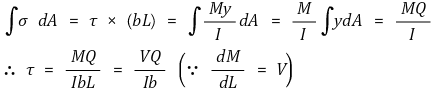
② 원형단면 보의 경우 최대 전단응력 τmax는 평균 전단응력 τmean의 (4/3)배
3. 카스틸리아노의 정리(Castigilano's theorem) [목차]
⑴ 정의 : 변형에너지의 힘에 관한 도함수는 변위로 표시된다는 정리
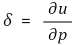
⑵ (참고) 균일강도 보는 균일단면 보보다 3배 더 많은 탄성에너지를 저장할 수 있음
⑶ (참고) 부하의 방향과 변위의 방향이 같아야 함
입력: 2020.08.05 08:18
'▶ 자연과학 > ▷ 재료역학·고체역학' 카테고리의 다른 글
| 【재료역학】 재료역학 목차 (0) | 2020.06.30 |
|---|---|
| 【재료역학】 10강. 리올로지 (1) | 2020.06.30 |
| 【재료역학】 7강. 비틀림 (0) | 2020.06.30 |
| 【재료역학】 6강. 모어 원 (0) | 2020.06.30 |
| 【재료역학】 4강. 인장과 압축 (0) | 2020.06.30 |







최근댓글