【재료역학】 10강. 리올로지

10강. 리올로지(rheology)

 

추천글 : 【재료역학】 재료역학 목차 

---

1. 개요 [본문]

2. 완전 탄성체 모형 [본문]

3. 맥스웰 모형 [본문]

4. 켈빈 모형 [본문]

5. 일반화된 맥스웰 모형 [본문]

6. 일반화된 켈빈 모형 [본문]

7. 버거스 모형 [본문]

---

 

1. 개요 [목차]

⑴ 점탄성(viscoelastic property) = 점성 + 탄성

① 점성 : 점성유체와 관한 특성

② 탄성 : 외력에 대해 탄성체가 보이는 특성

③ 선형 점탄성 : 변형률과 응력 사이에 비례관계와 중첩의 원리가 성립하는 경우

④ 비선형 점탄성 : 응력-변형률 곡선이 작용시간, 응력의 크기 등에 영향을 받는 경우

⑵ 리올로지 : 점탄성 물체의 변형 또는 유동을 다루는 학문 

⑶ 리올로지 모형 = 스프링 + 대시포트 

① 탄성의 역학적 모형 : 스프링(spring)

② 점성의 역학적 모형 : 대시포트(dashpot) 

⑷ 훅의 법칙과 옴의 법칙의 유사성

 

 

 

2. 모형 1. 완전 탄성체 모형(perfectly elastic body model, Hookean body model) [목차]

⑴ 정의 : 응력이 변형에 직선적으로 비례하는 역학적 모형

 

출처 : 서울대학교 생체물성공학 및 실험 수업

Figure. 1. 완전 탄성체 모형 및 응력-변형률-시간 곡선^]

 

⑵ 탄성계수(modulus of elasticity, Young's modulus)

① 인장 또는 압축에 의한 인장응력 또는 압축응력을 받는 경우

② 탄성계수 E, 응력 σ, 변형률 ε에 대하여,

 

 

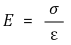
⑶ 전단탄성계수(shear modulus, modulus of rigidity)

① 비틀림에 의한 전단응력을 받는 경우 

② 전단탄성계수 G, 전단응력 τ, 전단변형률 γ에 대하여,

 

 

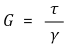
⑷ 체적탄성계수(bulk modulus)

① 유체 속에서 유체의 압력을 받는 경우

② 체적탄성계수 K_v, 유체의 압력 P, 체적 변형률 ε_v, 물체의 체적 변화량 Δv, 원래의 체적 v에 대하여,

 

 

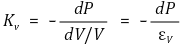
③ 등온압축률(isothermal compressibility) : 체적탄성계수의 역수

⑸ 포아송 비(Poisson's ratio)

 

 

 

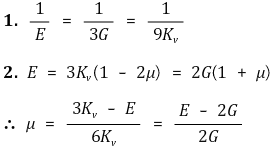
3. 모형 2. 맥스웰 모형(Maxwell model) [목차]

⑴ 정의 : 스프링 요소와 대시포트 요소가 직렬로 연결된 역학적 모형

 

출처 : 금동혁, 수확후 공정공학, 도서출판 씨아이알, 2008

Figure. 2. 맥스웰 모형 및 응력-변형률-시간곡선^]

 

① 초기 : 스프링 요소에 의한 탄성변형률이 발생

② 나중 : 대시포트에 의한 점성변형률이 발생

③ 응력 제거 후 : 스프링 요소에 의한 변형 ε_e는 회복됨. 대시포트에 의한 변형 ε_v는 회복되지 않음

⑵ 응력이완(stress relaxation)

① 정의 : 변형률이 일정할 때 응력이 서서히 감소하는 현상  

② 수식화

 

 

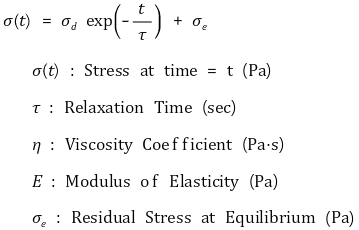
③ 유도

 

 

 

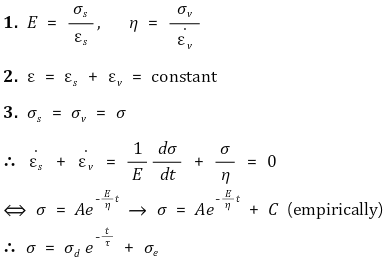
4. 모형 3. 켈빈 모형(Kelvin model) [목차]

⑴ 정의 : 스프링 요소와 대시포트 요소가 병렬로 연결된 역학적 모형 

 

출처 : 금동혁, 수확후 공정공학, 도서출판 씨아이알, 2008

Figure. 3. 켈빈 모형 및 응력-변형률-시간곡선^]

 

① 처음 : 전체 응력을 스프링과 대시포트가 분담. 스프링에 변형률이 없어도 대시포트 응력만으로 전체 응력을 커버함

② 나중 : 작용시간이 길어지면 손상이 발생할 수 있음

③ 응력 제거 후 : 스프링에 저장된 에너지가 대시포트로 전이되어 시간에 따라 곡선적으로 회복

⑵ 크리프 현상(creep phenomenon) : 응력이 일정할 때 시간에 따른 변형량이 증가하는 현상 

① 크리프 현상에 의해 점탄성으로 인해 ε-σ 곡선이 위로 볼록한 증가함수를 그림

○ (참고) 크리프라는 말은 그래프가 마치 기어가는 듯 하다고 해서 붙여짐 

○ 온도, 응력, 시간과의 관계

② 수식화

 

 

③ 유도 

 

 

④ 크리프 실험장치

 

출처 : 서울대학교 생체물성공학 및 실험 수업

Figure. 4. 크리프 실험장치^]

 

 

5. 모형 4. 일반화된 맥스웰 모형(generalized Maxwell model) [목차]

⑴ 정의 : 맥스웰 모형을 병렬로 연결한 모형. 맥스웰 모형만으로 선형 점탄성 거동을 충분히 표현 불가

 

출처 : 금동혁, 수확후 공정공학, 도서출판 씨아이알, 2008

Figure. 5. 일반화된 맥스웰 모형

 

⑵ 응력이완

 

 

 

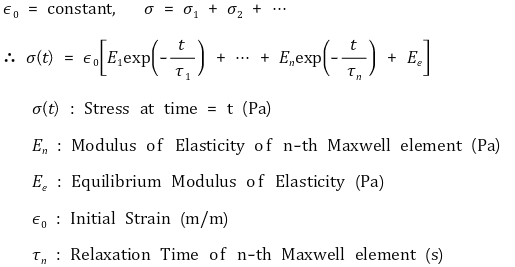
6. 모형 5. 일반화된 켈빈 모형(generalized Kelvin model) [목차]

⑴ 정의 : 켈빈 모형을 직렬로 연결한 모형

 

출처 : 금동혁, 수확후 공정공학, 도서출판 씨아이알, 2008

Figure. 6. 일반화된 켈빈 모형^]

 

⑵ 크리프 현상

 

 

 

7. 모형 6. 버거스 모형(Burgers model) [목차]

⑴ 정의 : 맥스웰 모형과 켈빈 모형을 직렬로 연결한 것. 또는 이 단위체들의 병렬연결

 

출처 : 금동혁, 수확후 공정공학, 도서출판 씨아이알, 2008

Figure. 7. 버거스 모형^]

 

⑵ 특징 : 대부분의 리올로지 특성을 설명할 수 있음 

 

 

입력: 2019.09.11 15:46